• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Площина. Точка і лінія в площині

Будь-яку площину визначають: 1) три точки, що не належать одній прямій; 2) пряма і точка, що не належить прямій; 3) дві прямі, що перетинаються; 4) дві паралельні прямі; 5) будь-який відсік площини, наприклад у вигляді трикутника.

На комплексному кресленні площини задають за допомогою відповідних проекцій геометричних фігур, що визначають площину.

Відносно площин проекцій площина може займати: 1) загальне положення – не перпендикулярне жодній з площин проекцій; 2) положення рівня – паралельне одній площини проекцій; 3) проекцію вальне положення – перпендикулярне до однієї площини проекцій.

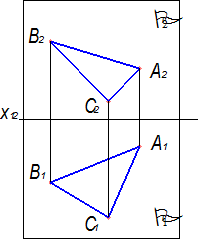
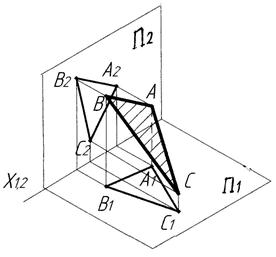Послідовність утворення прямокутних проекцій площини загального положення, яка визначена трикутником ABC, показана на рис. 1.13, а,б,в.

а)

в)

б)

Рисунок 1.13 - Прямокутні проекції площини загального положення

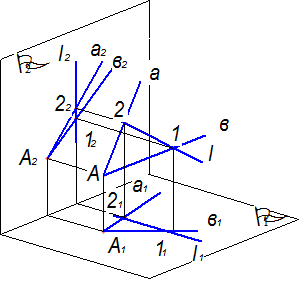
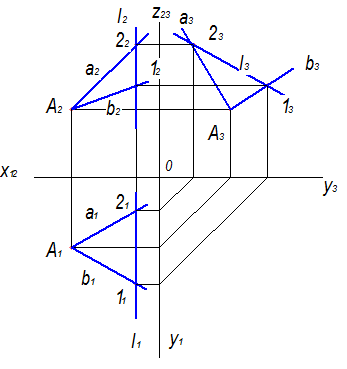
Пряма, належить площині за умови належності її будь-яких двох точок такій площині. На рис. 1.14,а показана площина, яка визначена двома прямими a і b, та пряма ℓ. Спільними точками між площиною та прямою є точки 1 і 2. На комплексному кресленні проекції прямої, що належить заданій площині, обов’язково проходять через відповідні проекції точок, яки також належать площині:ℓ(12)→[ ℓ1(1121), ℓ2(1222)] (див. рис. 1.14,б).

а)

б)

Рисунок 1.14 - Побудова лінії в площині загального положення

Точка належить площині, якщо вона належить будь-який прямій в заданій площині. На рис. 1.15, а,б,в показана площина, визначена трикутником ABC, та побудова проекцій точки D в площині за допомогою допоміжної прямої ℓ(А1)→[ ℓ1(А111), ℓ2(А212)]

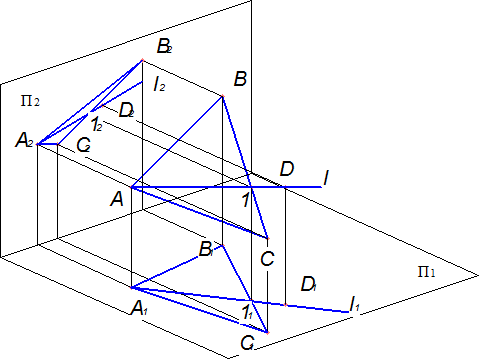
а)

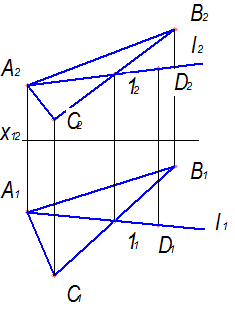
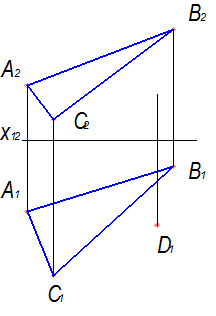
б) в)

Рисунок 1.15 - Побудова проекцій точки, яка належить площині

Читайте також:

1. Але відмінні від значення функції в точці або значення не існує, то точка називається точкою усувного розриву функції .
2. А–в горизонтальній площині; б – у вертикальній площині
3. Бюджетна лінія
4. В однорідному середовищі світло розповсюджується по прямим лініям.
5. Визначення зон і місць пошкодження в кабельних лініях
6. Визначення. Точка О називається полюсом, а промінь l – полярною віссю.
7. Визначення. Точки максимуму й мінімуму функції називаються точками екстремуму.
8. Відстань від точки до площини і від точки до прямої на площині
9. Втрати потужності та енергії в лініях
10. Геометрична інтерпретація розв’язків цілочислових задач лінійного програмування на площині
11. Графічне позначення матеріалу в перерізах і на виді - штрихування, що виконується тонкими суцільними лініями.
12. Живопис – це зображення на площині картин реального світу, які переформовуються у творчій уяві художника.

Переглядів: 2458