• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Метод заміни площин проекцій

Розв’язання метричних задач можна звести до чотирьох основних типів:

1) перетворення прямої загального положення в пряму рівня;

2) перетворення прямої загального положення в проекціювальну;

3) перетворення площини загального положення в проекціювальну;

перетворення площини загального положення в площину рівня.

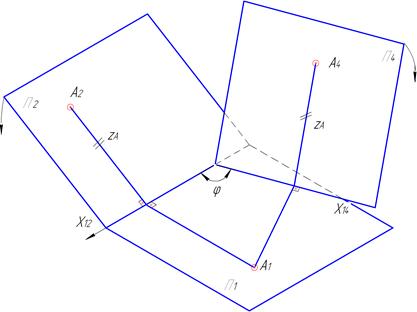
Найбільш поширені методи, що використовуються для цього – метод заміни площин проекцій та метод плоско-паралельного переміщення. Метод заміни площин проекцій полягає в тому, що вводиться допоміжна площина проекцій, яка перпендикулярна тільки до однієї з площин проекцій (горизонтальної Π₁, фронтальної Π₂, профільної Π₃) (рис. 4.1, 4.2).

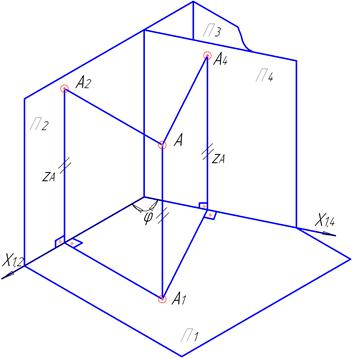
Рисунок 4.1 – Система основних та додаткових площин проекцій:

Π₄ – додаткова площина проекцій, що перпендикулярна тільки до Π₁

Для переведення відрізка прямої із загального положення в положення рівня для визначення, наприклад, натуральної довжини, необхідно ввести додаткову площину паралельно одній з проекцій відрізка (рис. 4.3, 4.4).

a

б

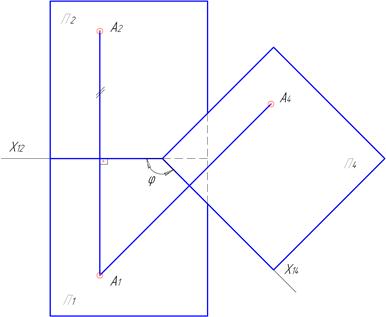
Рисунок 4.2 – Утворення плоскої моделі систем площин проекцій: а – проміжний етап трансформації; б – плоска модель, що утворена в результаті трансформації

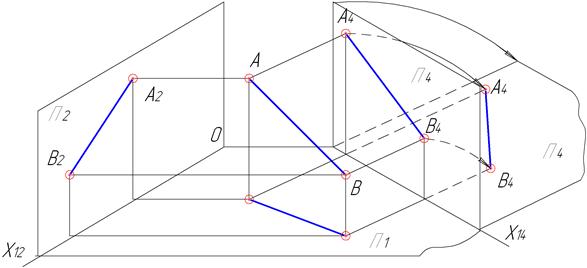
Рисунок 4.3 – Введення додаткової площини проекцій для визначення довжини відрізка загального положення

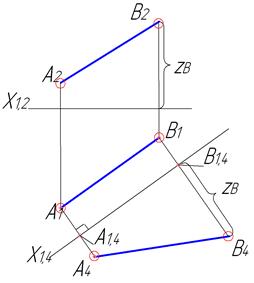
Рисунок 4.4 – Визначення довжини відрізка за умови задання АВ (А₁В₁, А₂В₂)

Для того, щоб перетворити пряму загального положення в проекціювальне положення необхідно ввести допоміжну площину перпендикулярно до проекції відрізка, яка є його натуральною величиною (рис.4.5, 4.6). Якщо пряма займає загальне положення, то переведення в проекціювальне положення відбувається в два етапи: спочатку в пряму рівня, а потім в проекціювальну пряму.

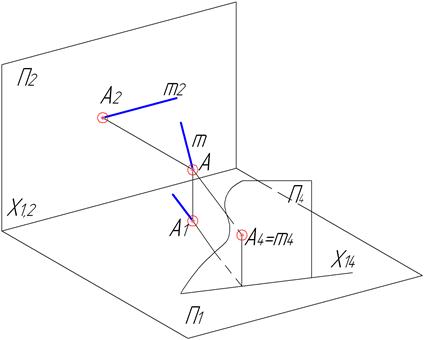
Рисунок 4.5 – Перетворення прямої рівня в проекціювальну пряму (наочне зображення)

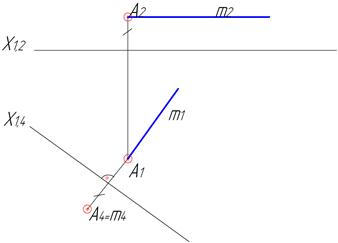
Рисунок 4.6 – Перетворення прямої рівня в проекціювальну пряму (комплексне креслення)

Для переведення площини із загального положення в проекціювальне та в площину рівня необхідно застосувати такий алгоритм (рис.4.7):

1) вводимо горизонталь або фронталь;

2) вводимо допоміжну площину проекцій перпендикулярно до горизонтальної проекції горизонталі;

3) переводимо площину в проекціювальне положення;

4) вводимо нову допоміжну площину паралельно площині в проекціювальному положенні;

5) переводимо площину в натуральну величину.

Розглянемо геометричні підстави для розв’язання деяких метричних задач.

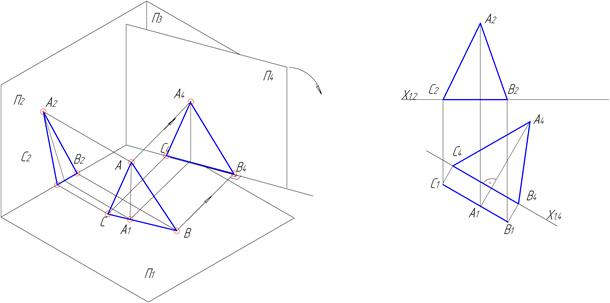
Рисунок 4.7 – Перетворення проекціювальної площини в площину рівня

Для визначення відстані між двома паралельними прямими необхідно перевести обидві прямі в проекціювальне положення (рис. 4.8). Якщо прямі займають загальне положення, то необхідно провести два послідовних перетворення: спочатку ввести додаткову площину для переведення прямих в натуральну величину, а потім ввести додаткову площину перпендикулярно до отриманих проекцій прямих.

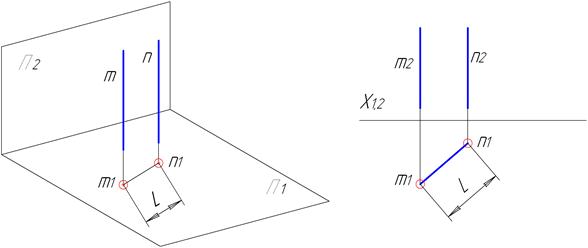
Рисунок 4.8 – Визначення відстані між двома паралельними прямими

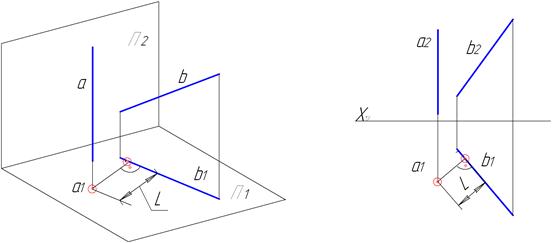
Рисунок 4.9 – Визначення відстані між двома мимобіжними прямими

Для визначення відстані між двома мимобіжними прямими необхідно знайти найкоротшу відстань. Для цього необхідно виконати перетворення таким чином, щоб одна з прямих зайняла проекціювальне положення, тобто спроекціювалася в точку. Перпендикуляр з цієї точки визначає шукану відстань (рис.4.9). Якщо обидві прямі початково займають загальне положення, то перетворення відбувається в два етапи: 1) вводиться додаткова площина проекцій таким чином, щоб одна з прямих спроекціювалась в натуральну величину; 2) вводиться додаткова площина перпендикулярно до отриманої натуральної величини.

Для визначення відстані між точкою та площиною необхідно перетворити площину в проекціювальне положення та опустити перпендикуляр з отриманої проекції точки на пряму, що є проекцією площини (рис.4.10). Якщо площина займає загальне положення, то потрібно спочатку перевести задану площину в проекціювальне положення (рис.4.7).

Рисунок 4.10 – Визначення відстані між точкою та площиною

Для визначення величини двогранного кута між площинами необхідно ввести додаткову площину перпендикулярно до ребра, при якому визначається кут, тобто перевести вказане ребро в проекціювальне положення. При цьому кожна площина спроекціюється в пряму (рис.4.11). Якщо ребро при двогранному куті займає загальне положення, то потрібно спочатку перевести його в натуральну величину, а вже потім – в точку.

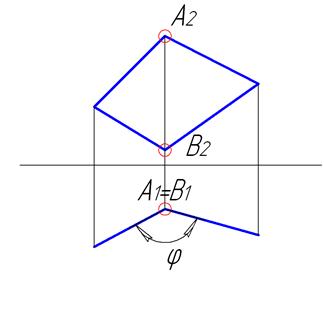
Рисунок 4.11 – Визначення величини двогранного кута між площинами

Читайте також:

1. D) методу мозкового штурму.
2. H) інноваційний менеджмент – це сукупність організаційно-економічних методів управління всіма стадіями інноваційного процесу.
3. I Метод Шеннона-Фано
4. I. ЗАГАЛЬНІ МЕТОДИЧНІ ВКАЗІВКИ
5. I. Метод рiвних вiдрiзкiв.
6. VII. Нахождение общего решения методом характеристик
7. А. науковий факт, b. гіпотеза, с. метод
8. Автоматизація водорозподілу на відкритих зрошувальних системах. Методи керування водорозподілом. Вимірювання рівня води. Вимірювання витрати.
9. Агрегативна стійкість, коагуляція суспензій. Методи отримання.
10. Агресивний тип дивідендної політики включає метод стабільного приросту дивідендів і метод постійного коефіцієнта виплат.
11. АгротехнІЧНИЙ метод
12. Адаптовані й специфічні методи дослідження у журналістикознавстві

Переглядів: 3684