• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Загальна характеристика формоутворення кривих ліній та кривих поверхонь

Крива лінія – це геометричне місце послідовних положень точки, що здійснює неперервний рух в просторі. При утворенні кривої лінії у такий спосіб її можна подати у вигляді множини точок, які їй належать, і відобразити на комплексному кресленні як сукупність відповідних проекцій окремих точок множини, що показано на рис.5.1.

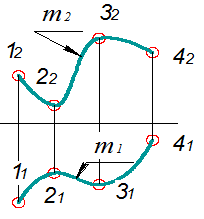
Рисунок 5.1 - Комплексне креслення кривої лінії

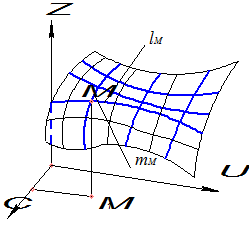Криву поверхню можна розглядати як траєкторію переміщення деякої лінії ( твірної), що здійснює неперервний рух в просторі. Деякі поверхні утворюються внаслідок руху лінії постійної форми, інші так, що твірна разом зі зміною положення в просторі змінює також і свою форму. Поверхню, показану на рис. 5.2, у такому випадку розглядають як однопараметричну множину твірних {ℓ}.

Закон переміщення твірної зручно задавати деякими сталими лініями, що мають назву напрямних ліній.

Рисунок 5.2 – Каркас кривої поверхні

Кожна точка твірної при її русі описує деяку лінію m, сукупність яких складає також однопараметричну множину {m} (див. рис. 5.2 ).

З кривих ℓi та mi складається так званий сітчастий каркас кінематичної

поверхні. Якщо врахувати неперервне переміщення твірної, а відповідно, неперервність і самої поверхні, то можна зробити висновок: через будь-яку точку М поверхні можна провести пару кривих ℓм і mм.

Сукупність умов, необхідних і достатніх для задання поверхні, називається визначником поверхні. Останній складається з геометричної та алгоритмічної частин. Геометричною частиною визначника поверхні є геометричні фігури, які беруть участь в утворенні поверхні. Алгоритмічна частина – це сукупність правил застосування геометричної частини визначника для утворення поверхні.

Велика кількість різноманітних поверхонь, які використовують в інженерній практиці, потребує їх систематизації. Це особливо важливо в автоматизованому проектуванні при створенні інформаційних систем. В кінематичному способі утворення поверхонь цілком природно в основу систематизації покласти форму твірної лінії і закон її переміщення. Тому за формою твірної розрізняють лінійчаті (твірна – пряма), криволінійні (твірна – крива), за законом переміщення твірної – поверхні обертання, поверхні переносу і гвинтові.

Читайте також:

1. DIMCLRE (РЗМЦВЛ) - колір виносних ліній (номер кольору). Може приймати значенняBYBLOCK (ПОБЛОКУ) і BYLAYER (ПОСЛОЮ).
2. I. Загальна характеристика політичної та правової думки античної Греції.
3. II. ВИРОБНИЧА ХАРАКТЕРИСТИКА ПРОФЕСІЇ
4. II. Критерій найбільших лінійних деформацій
5. II. Морфофункціональна характеристика відділів головного мозку
6. Ni - загальна кількість періодів, протягом яких діє процентна ставка ri.
7. А. Це наявність в однієї людини кількох ліній клітин з різним набором хромосом.
8. Аварії на хімічно-небезпечних об’єктах та характеристика зон хімічного зараження.
9. Автобіографія. Резюме. Характеристика. Рекомендаційний лист
10. Автокореляційна характеристика системи
11. Активний опір ліній електропередачі
12. Амплітудно-частотна характеристика, смуга пропускання і загасання

Переглядів: 987