• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Розв’язання задачі.

Підставляємо дані в (3.6) та виконуємо розрахунок:

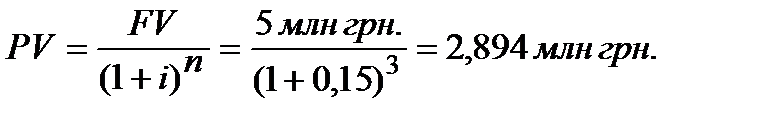
Відповідь: Для того, щоб через 3 роки мати на рахунку 5 млн грн при процентній ставці 20%, необхідно покласти в банк на рахунок 2,894 млн грн.

Показник 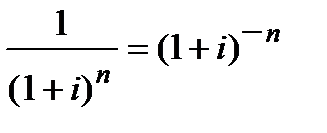в літературі називають також, як і при простому дисконтуванні, дисконтним або дисконтуючим множником (discount factor). Ще можуть іменувати його обліковим множником. Така «вільна» термінологія чітко не виділяє, чи це множник з простими процентами, чи зі складними, чи це множник з використанням процентної, чи облікової ставки. Більш однозначним інформаційним терміном цього показника, на наш погляд, є вираз ─ складний дисконтний множник.

Економічна суть складного дисконтного множника є такою: він показує «теперішню» ціну майбутньої однієї грошової одиниці (1 грн, 1 $, тощо), тобто, чому дорівнює сьогодні одна грошова одиниця, що обертається у сфері бізнесу n періодів попереду від моменту сьогоднішнього розрахунку, при заданій процентній ставці (доходності) і.

У випадку, коли процентні ставки в періодах нарахування різняться, а періоди нарахування процентів згруповані за ознакою рівності між собою ( 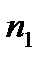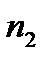… 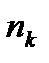), тобто, якщо процентна ставка перемінна, а саме:

─ протягом 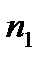періодів процентна ставка дорівнює ,

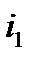─ протягом 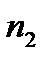періодів процентна ставка дорівнює ,

……………………………………………………………

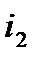─ протягом 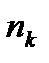періодів процентна ставка дорівнює ,

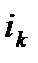то від формули (2.10) формула складного дисконтування приймає вигляд:

; (3.7)

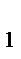де і 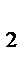, і ,…і ─ процентні ставки за періоди 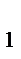n , n 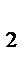, … …, n 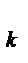,відповідно.

Нагадуємо, що при нарахуванні складних процентів за ціле й дробове число періодів нарахування процентів застосовується формула змішаного нарахування процентів(2.15). Від формули (2.15) формула складного дисконтування приймає вигляд:

(3.8)

деFV, PV, i – мають зміст той же, що й у формулах (2.2), (2.10), (3.6), (3.7);

k– ціла частина кількості періодів нарахування;

f – дробова частина кількості періодів нарахування процентів.

Раніше згадувалось, що різницю ( 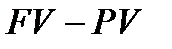) можемо розглядати не тільки, як нарощення, не тільки як процент, нарахований на PV, а і як дисконт з суми FV. Показник ─ «дисконт з суми FV» при використанні складної процентної ставки наділимо позначкою D 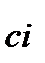(Discount of compound interest ):

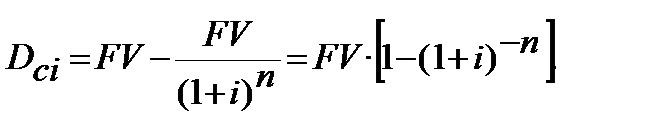(3.9)

Формула (3.9) може мати інший вигляд:

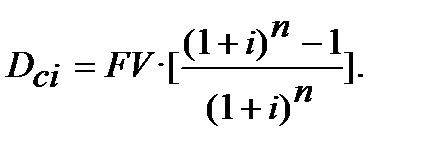(3.9*)

Формула (3.9), (3.9*) дає можливість розраховувати при складному дисконтуванні дисконт 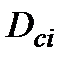(складний дисконтний процент) від FV не обчислюючи PV.

Цікавим є момент, що при FV = 1 (1 грн, 1 $, одна грошова одиниця), n = 1 (один рік, або один період нарахування) з формули (3.9) виходить той же результат що і з формули (3.4), а саме, формула (3.5).

Приведена вартість є однією з багатьох і, в той же час, однією з основних характеристик фінансового аналізу.

Розрахунок приведеної вартості має свої особливості:

─ зростання n зменшує розмір приведеної вартості;

─ збільшення і також зменшує розмір приведеної вартості.

Розрахунок приведеної вартості має у фінансах велику кількість напрямів застосування.

Розкриємо один з напрямів застосування розрахунку приведеної вартості на прикладі Модельної задачі 4.

Читайте також:

1. IV. Перевірка розв’язання і відповідь
2. Алгоритм розв’язання задачі
3. Алгоритм розв’язання розподільної задачі
4. Визначення оптимального варіанта розв’язання проблеми на основі порівняльного аналізу можливих варіантів
5. Визначення проблеми, на розв’язання якої спрямована Програма
6. Відповіді на ситуаційні задачі.
7. Відповіді на ситуаційні задачі.
8. Геофізичний контроль за розробкою нафтових і газових родовищ. Задачі. Методи і методика дослідження
9. Гіпотеза як один із важливих варіантів розв’язання наукової проблеми.
10. Для всіх , та , то він є оптимальним планом транспортної задачі.
11. За допомогою теорії розмірностей розмірні фізичні величини, що входять в опис фізичного процесу, комбінуються в безрозмiрнi комплекси, які можна розглядати як нові змінні задачі.
12. Загальні рекомендації до розв’язання задач

Переглядів: 600