Номінальна процентна ставка у механізмі складного нарахування процентів.

Розглянемо формулу (2.10), ─ формулу складного нарахування процентів з використанням процентної ставки:

FV = PV ·(1 + і) 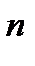. (2.10)

Нас цікавить показники «і»та «n». У формулі (2.10) надано таке їх визначення:

i– процентна ставка у кожному з періодів нарахування процентів n (у формулі показник i використовується не у відсотках, а десятковим дробом, в частках, в долях);

n – кількість періодів нарахування процентів впродовж часу (строку) застосування ставки і; також, у кожному з цих періодів процентні ставки рівні між собою.

У формулі (2.10) є жорсткий, можна сказати закономірний зв’язок між «n» та «і». Основою зв’язку є показник ─ період нарахування процентів. В залежності від періоду нарахування процентів визначаються кількісно «n» та «і». Якщо період нарахування процентів ─ квартал, то «і» ─ чисельний показник за квартал, і «n» ─ кількість кварталів. Якщо період нарахування процентів ─ півріччя, то «і» ─ процентна ставка за півріччя, і «n» ─ кількість півріч. Саме цей механізм взаємозв’язку між «n» та «і» і відображено у їх визначенні у формулі (2.10).

Якщо зафіксувати у (2.10), що показник «і» записується у формулу тільки як показник річної ставки, тобто «і» завжди номінальна, (а вона, як правило, так і надається), а період нарахування процентів не річний, а інший (півріччя, квартал, будь-який інший), то, щоб записати в дужках формули (2.10) правильний чисельний показник процентної ставки, необхідно річну (номінальну) «і» перераховувати на відповідну (піврічну, квартальну, будь-яку іншу). З цією метою в фінансових розрахунках введено показник «m» ─ кількість періодів нарахування процентів у році. Тоді, при нарахуванні процентів «m» разів у році, формула (2.10) приймає такий вигляд:

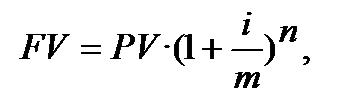(6.1)

де i– номінальна (річна) процентна ставка (у формулі показник i використовується не у відсотках, а десятковим дробом, в частках, в долях);

m ─ кількість періодів нарахування процентів у році;

n – кількість періодів нарахування процентів впродовж строку.

Досить часто строк надається в роках. Якщо строк фінансової операції (Т), наданий в роках (N), внести в формулу (6.1), то формулу (6.1) можна навести у такому варіанті:

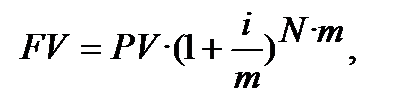(6.2)

m ─ кількість періодів нарахування процентів у році;

N ─ кількість років впродовж строку.

_Приклад 6.2___________________________________

Депозит в розмірі 500 тис. грн внесено в банк на 5 років під 10% річних (складні проценти). Нарахування процентів щоквартальне. Знайти нарощену суму.

Розв’язуємо за допомогою формули (6.2).

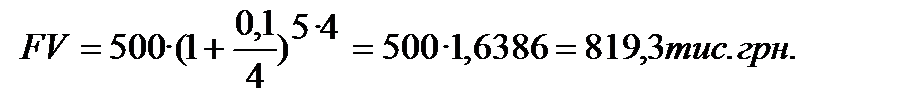
При збільшенні кількості періодів нарахування процентів у році (m ─ зростає) ─сума нарощення зростає. Якщо в умови Прикладу 6.2 внести зміну ─ нарахування процентів проводити щомісячно, то нарощена сума буде дорівнювати:

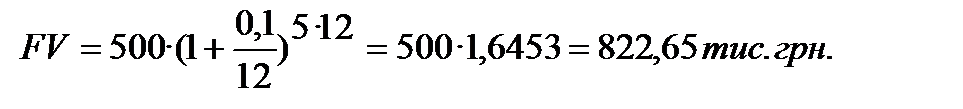
Про таку закономірність вже згадувалося у висновках пункту 2.2.1 (стор. 88). Поділ строку фінансової операціїна більшу кількість періодів нарахування процентів при застосуванні механізму нарахування складних процентів забезпечує в кінцевому результаті більший розмір нарощеної суми. Для ілюстрації такого висновку приведемо значення множника (1+і/m) в ступені N·m для і=20% і N=10 років при різних m в межах року, табл. 6.1:

Таблиця 6.1 ─ Зміна коефіцієнта нарощення при

ставці і =20% і строку N = 10 років.

Кількість періодів нарахування процентів у році: m
Коефіцієнт нарощення	6,1917	6,7275	7,04	7,2682	7,385

З наведених в табл. 6.1 даних найбільше «наростання» при нарощенні дає перехід від щорічного нарахування процентів до піврічного, найменший «ефект наростання» ─ перехід від щомісячного до щоденного.

Характеристику номінальної ставки завершимо двома зауваженнями.

По-перше, формули (6.1) та (6.2) є похідними, вони є варіантами формули (2.10), а не навпаки, як це зазвичай вважається.

По-друге, у формулі (2.10) у визначенні чисельного показнику процентної ставки «і» точно не зазначено, яка це ставка, річна, чи будь-яка інша. З такого визначення можна зробити хибний висновок, що в формулі (2.10) при її практичному застосуванні чисельний показник процентної ставки «і» може бути як річним так і будь-яким, відмінним від річного, ─ піврічним, квартальним, місячним, тощо. Таке може бути, але не завжди і, зазвичай, рідко. В формулі (2.10) чисельний показник процентної ставки «і», як правило, має за свою основу, а тому і в своїй структурі, показник процентної ставки «і», і саме річної «і», і тому, при підстановці у формулу (2.10) дійсного чисельного розміру «і», як правило, там вже присутній показник процентної ставки «і» і не будь-якої, а саме річної. Тому, в практичних розрахунках за формулою (2.10), як правило, використовується річна процентна ставка «і», тобто в формулі (2.10) при фактичних розрахунках присутня лише номінальна ставка. Таке ствердження потребує пояснення.

_Додаткова інформація_________________________

Пояснення, що в формулі (2.10) показник в дужках «і» відображає собою, віддзеркалює собою показник річної процентної ставки, а, отже, представляє себе через номінальну (річну) ставку, треба починати з показника «n».

В багатьох підручниках і навчальних посібниках показник «n» визначається одночасно і як строк, і як кількість років нарощення (Четыркин [15, стор. 43]), (Гриценко [3, стор. 90]). У Бакаєва [1] на сторінці 12 «n» ─ кількість років, а на сторінці 13 «n» ─ періоди, впродовж яких використовуються відповідні ставки, ─ а це вже не кількість років, а кількість періодів нарахування процентів. Далі, у Бакаєва, на цій же 13-й сторінці і далі по тексту, наприклад на 15-й сторінці «n» ─ це знову кількість років. Якщо взяти Долінського [6], Машину [9], Медведєва [10], Мелкумова [11], то в цих джерелах про «n» говориться, що це періоди, і, скоріш за все, ─ це треба розуміти як кількість періодів, де періодом може бути не тільки рік. Кутуков [8, стор. 23] надав визначення «n» в такій редакції: «… n ─ кількість періодів нарахування процентів (якщо проценти капіталізуються один раз за рік, то n ─ кількість років нарощення).» Таке визначення «n» у Кутукова яскраво демонструє, що «n» показує не тільки кількість років, а і кількість інших періодів нарахування процентів (кількість півріч, кількість кварталів, кількість місяців, кількість будь яких інших періодів нарахування процентів). Автор цього посібника цілком згоден з Катуковим, тобто, якщо показник «n» відображає кількість років нарощення процентів, то це лише один варіант з переліку можливих варіантів, що кількісно характеризує показник «n». Нагадуємо, що в згаданих підручниках і посібниках мова йде про показник ступеню «n» в одній і тій же формулі, а точніше, про один і той же формальний вираз, який ідентичний нашому запису формули (2.10). Справа в тому, що при визначенні показника «n» науковці і викладачі не пов’язували визначення «n» з визначенням «і». Але, між «n» та «і» у формулі (2.10) існує жорсткий зв’язок.

Зв’язок такий:

─ якщо проценти нараховуються кожного року, то «n» ─ кількість років і в дужках 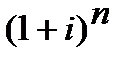показник «і» ─ процентна ставка за рік, або річна;

─ якщо проценти нараховуються кожного півріччя, то «n» ─ кількість півріч і в дужках 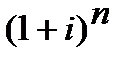на місці показнику «і» ─ використовується процентна ставка за півріччя, або піврічна. Щоб знайти чисельно процентну ставку за півріччя треба річну процентну ставку «і» поділити на 2 (в році два півріччя) і, відповідно, показник в дужках приймає такий вигляд 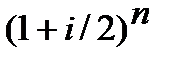. Звертаємо увагу, що у виразі 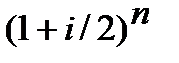величина «і» ─ річна процентна ставка;

─ якщо нарахування процентів щоквартальне, то «n» ─ кількість кварталів і в дужках 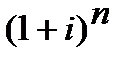на місці показнику «і» ─ «працює» процентна ставка за квартал, або квартальна. Щоб знайти чисельно процентну ставку за квартал треба річну процентну ставку «і» поділити на 4 (в році чотири квартали) і, відповідно, показник в дужках приймає такий вигляд . Знову звертаємо увагу, що у виразі величина «і» залишається показником річної процентної ставки;

─ аналогічно, якщо нарахування процентів щомісячне, то «n» ─ кількість місяців і в дужках 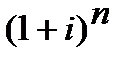на місці показнику «і» ─ «формула вимагає» використання місячної процентної ставки. Щоб знайти процентну ставку за місяць треба річну процентну ставку «і» поділити на 12 (в році дванадцять місяців) і, відповідно, показник в дужках приймає такий вигляд 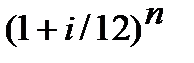. Також, як і в попередніх нарахуваннях, у виразі 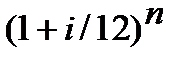величина «і» залишається показником річної процентної ставки.

Наведений в попередньому абзаці механізм зв’язку між «n» та «і» з самого початку, ще з механізму її виникнення закладено у формулі (2.10). Цей жорсткий зв’язок є атрибутом формули (2.10), який не тільки може, а й необхідно повинен бути відображений шляхом визначення «n» та «і» в їх взаємозв’язку. Саме така необхідність й примусила сформулювати визначення «n» та «і» так, як це надано у формулі (2.10). Визначення, що «…i– процентна ставка у кожному з періодів нарахування процентів n…», означає, що там де у формулі (2.10) стоїть позначка «і» необхідно підставити процентну ставку, що «притаманна», що «існує» впродовж періоду нарахування процентів «n», що відповідає періоду нарахування процентів «n». А у зв’язку з тим, що процентні ставки надаються, як правило, в т.ч. і за неоголошеними правилами, надаються як річні, то процентні ставки за період менше року або більше року розраховуються відповідно діленням річної ставки на частини або збільшенням річної ставки. Тому, у формулі (2.10) при підстановці на місце показника «і» чисельного значення як правило буде фігурувати показник річної процентної ставки.

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
Номінальна ставка та її використання у формулах фінансових розрахунків	\|	Номінальна облікова ставка у механізмі складного дисконтування процентів.

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.35 сек.