
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Розділ 8. ЕКВІВАЛЕНТНІСТЬ СТАВОК ПРОЦЕНТА
Один і той же фінансовий результат можна одержати різноманітними способами, використовуючи різні ставки, різні механізми нарощення та дисконтування. Таке є можливим тому, що будь-яка ставка процента (процентна, облікова або сила росту) характеризує один і той же показник ─ доходність фінансової операції.
Еквівалентні ставки─ це такі ставки, застосування яких приводить до однакових фінансових результатів.
Латинський термін «еквівалентний» означає ─ «рівноцінний», а, скоріше за все, на наш погляд, означає ─ рівно оцінюваний. Додержання «рівнооцінюваності» вимагає додержання певних принципів. Еквівалентні ставки, за визначенням, не змінюють початкову суму (PV=const), не змінюють кінцевий результат (FV=const), не змінюють строку операції (Т=const) і не змінюють кількості періодів нарахувань впродовж строку Т (n=const). Додержання таких вимог має у фінансах назву ─ принцип еквівалентності.
Іншими словами, еквівалентність ставок ─ це заміна однієї ставки на другу, заміна ставки, яка не змінює фінансових показників, тобто заміна ставки при дотриманні принципів еквівалентності.
Якщо початкові і кінцеві суми не змінюються, то не змінюється і їх різниця ─ прибуток (процент). При рівності початкових сум, процент визначається розміром множника нарощення. Звідси випливає: щоб вивести співвідношення для еквівалентних ставок, потрібно дорівняти множники нарощення для різних процентних ставок і з отриманої рівності виразити потрібний показник. Основних формул у фінансах всього чотири, тому, основних множників у нас також чотири. Для одержання формул еквівалентності ставок запишемо чотири множника у вигляді так званого квадрата еквівалентності, рис. 8.1.
Квадрат множників ставок процента

| 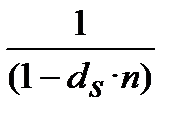
|
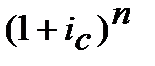
| 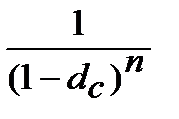
|
Можливі співвідношення ставок еквівалентності
 → ← → ← 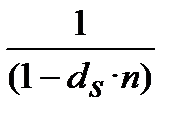 ↑ ↓↑ ↓
↑ ↓↑ ↓
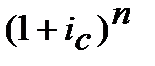 → ← → ← 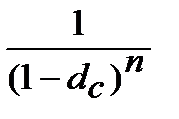
|
Рисунок 8.1 – Квадрат еквівалентності ставок процента: (де «і» ─ процентна ставка, «d» ─ облікова ставка, індекс «s» означає, що ставки «і» та «d» прості (від англ. simple), індекс «с» означає, що ставки «і» та «d» складні (від англ. compound)).
Квадрат еквівалентності дає можливість записати всі формули еквівалентності ставок. Використовуючи квадрат еквівалентності немає потреби запам’ятовувати формули. Просто при необхідності треба написати відповідне співвідношення між множниками нарощення й одержати з нього потрібну формулу. В квадраті еквівалентності можливі співвідношення між множниками нарощення вказані стрілками. Таких співвідношень всього дванадцять. Головне ─ зрозуміти цей простий прийом.
Еквівалентність простої процентної ставки (  ) і простої облікової ставки
) і простої облікової ставки 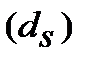 знайдемо з дорівнювання множників
знайдемо з дорівнювання множників  =
= 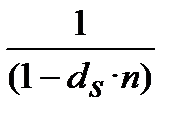 . Якщо n ─ ціле число, або ціле число з дробом, наприклад, кількість років, то:
. Якщо n ─ ціле число, або ціле число з дробом, наприклад, кількість років, то:
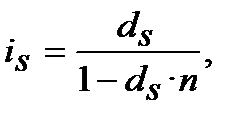 (8.1)
(8.1)
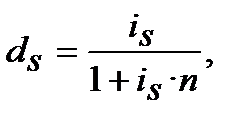 (8.2)
(8.2)
У формулах (8.1), (8.2) при умові, що n ─ кількість років, ставки  ,
, 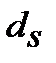 ─ річні, якщо n вимірюється кількістю півріч, ставки
─ річні, якщо n вимірюється кількістю півріч, ставки  ,
, 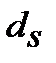 ─ піврічні, загалом, ставки відповідні періоду нарахування процентів.
─ піврічні, загалом, ставки відповідні періоду нарахування процентів.
Треба звернути увагу, що співвідношення еквівалентності між простими ставками залежать від строку. Наприклад, для 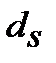 = 10%
= 10%  змінюється так, табл.8.1.
змінюється так, табл.8.1.
Таблиця 8.1 ─ Еквівалентність простої процентної ставки  до простої облікової, що дорівнює
до простої облікової, що дорівнює 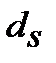 = 10%, в залежності від строку n (кількість років).
= 10%, в залежності від строку n (кількість років).
| n (кількість років) | 0,1 | 0,5 | |||||
 (%) (%)
| 10,1 | 10,5 | 11,1 | 12,5 | 33,3 | 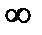 * *
|
*при n = 9 років  = 100%, а при 10-ти і більше роках формула (8.1) не працює, тобто еквівалентності ставок не існує.
= 100%, а при 10-ти і більше роках формула (8.1) не працює, тобто еквівалентності ставок не існує.
Якщо n ─ дробове число, наприклад, строк вимірюється в днях, тоді підставимо у (8.1) і (8.2) n = t /y та одержимо варіанти еквівалентності ставок (нагадуємо, що t ─ строк нарощення (дисконтування) процентів у днях, y ─ кількість днів у році, y ще може мати назву ─ часова база, або ─ база розрахунку).
Варіант 1. Бази розрахунків, тобто кількість днів у році y, ─ рівні в еквівалентних варіантах:
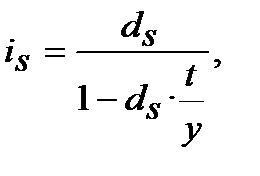 або
або 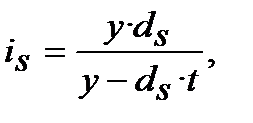 (8.3)
(8.3)
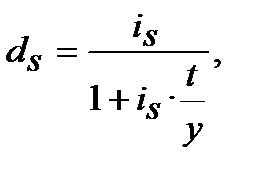 або
або 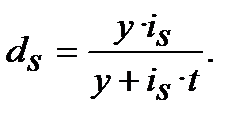 (8. 4)
(8. 4)
Варіант 2. Бази розрахунків, тобто кількість днів у році y, ─ різні в еквівалентних варіантах.
Якщо при процентній ставці  нарахування процентів здійснюється при y = 365 днів, а по обліковій ставці
нарахування процентів здійснюється при y = 365 днів, а по обліковій ставці 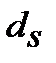 розрахунок проводиться при y = 360 днів, то формули еквівалентності мають такий вигляд:
розрахунок проводиться при y = 360 днів, то формули еквівалентності мають такий вигляд:
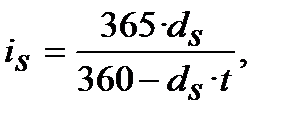 (8.5)
(8.5)
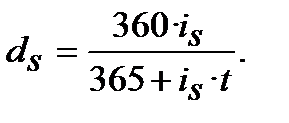 (8.6)
(8.6)
Якщо при процентній ставці  нарахування процентів здійснюється при y = 360 днів, а по обліковій ставці
нарахування процентів здійснюється при y = 360 днів, а по обліковій ставці 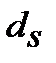 розрахунок проводиться при y = 365 днів, то формули еквівалентності мають такий вигляд:
розрахунок проводиться при y = 365 днів, то формули еквівалентності мають такий вигляд:
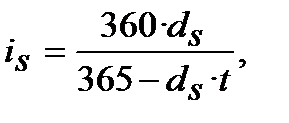 (8.7)
(8.7)
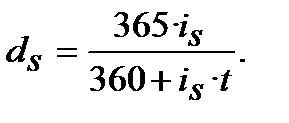 (8.8)
(8.8)
Забезпечення еквівалентності простих процентних та облікових ставок досягається, при інших рівних умовах, їх нерівністю, тобто завжди 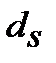 менше (чисельно, по модулю) еквівалентній до неї
менше (чисельно, по модулю) еквівалентній до неї  .
.
Еквівалентність процентних ставок ─ простої ставки (  ) і складної ставки(
) і складної ставки( 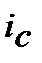 ), знайдемо з дорівнювання множників
), знайдемо з дорівнювання множників  =
= 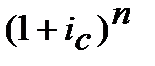 :
:
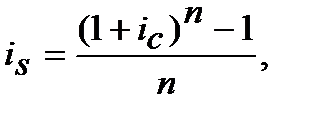 (8.9)
(8.9)
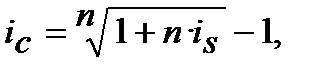 або
або 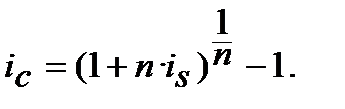 (8.10)
(8.10)
У формулах (8.9), (8.10) ставки  ,
, 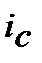 є ставками в періодах n. Якщо n вимірюється роками, то і ставки
є ставками в періодах n. Якщо n вимірюється роками, то і ставки  ,
, 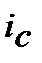 ─ річні, якщо n вимірюється кварталами, то, відповідно ставки
─ річні, якщо n вимірюється кварталами, то, відповідно ставки  та
та 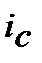 ─ квартальні, і така відповідність в цих формулах завжди. Якщо зафіксувати ставки тільки як номінальні, тобто річні, то, при m разів нарахування процентів у році і кількості років N , показник n = N · m. За таких умов формули (8.9) та (8.10) мають такий вигляд:
─ квартальні, і така відповідність в цих формулах завжди. Якщо зафіксувати ставки тільки як номінальні, тобто річні, то, при m разів нарахування процентів у році і кількості років N , показник n = N · m. За таких умов формули (8.9) та (8.10) мають такий вигляд:
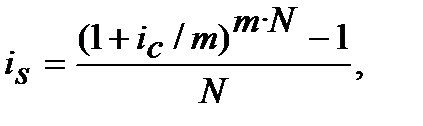 (8.11)
(8.11)
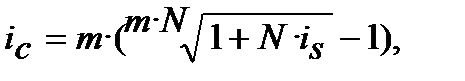 або
або
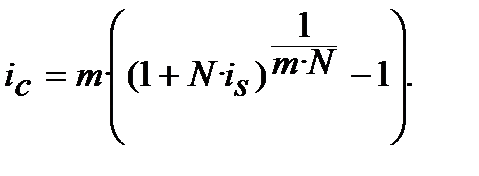 (8.12)
(8.12)
У формулах (8.11) та (8.12) ставки  та
та 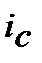 ─річні.
─річні.
Еквівалентність простої облікової ставки ( 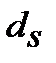 ) і складної процентної ставки(
) і складної процентної ставки( 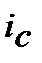 ), знайдемо з дорівнювання множників
), знайдемо з дорівнювання множників 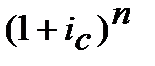 =
= 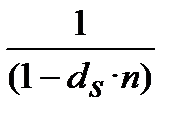 :
:
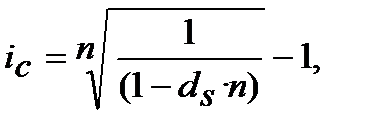 або
або 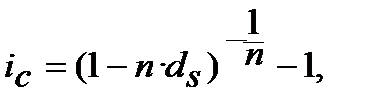 (8.13)
(8.13)
 (8.14)
(8.14)
Якщо зафіксувати ставки тільки як номінальні, тобто ─ річні, то при застосуванні m та N формули (8.13) та (8.14) набувають такого вигляду:
 або
або
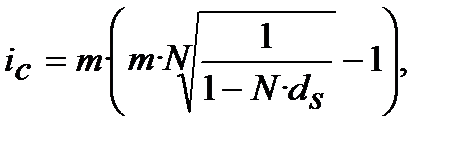 (8.15)
(8.15)
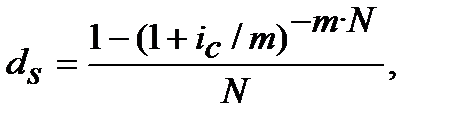 або
або
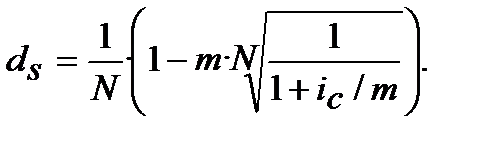 (8.16)
(8.16)
Еквівалентність складної процентної ставки( 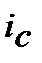 ) і складної облікової ставки (
) і складної облікової ставки ( 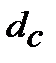 ) знайдемо з дорівнювання множників
) знайдемо з дорівнювання множників 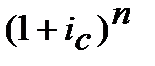 =
= 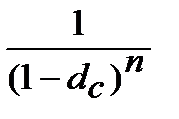 :
:
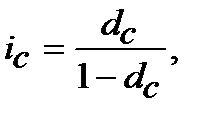 (8.17)
(8.17)
 (8.18)
(8.18)
Як бачимо, при виведенні формул (8.17) та (8.18) показник кількості періодів нарахування процентів ─ n в математичний запис формул не попадає, він там відсутній. Його відсутність в запису формул еквівалентності складних процентної та облікової ставок привела до некоректного висновку, що в формулах (8.17) та (8.18) результат еквівалентних перерахунків не залежить від строку фінансової операції, або, що одне і те ж, не залежить від кількості періодів нарахування чи утримання процентів. Такої думки дотримуються Долінський [6, стор. 22] Мелкумов [11, стор. 68], Четыркин [15, стор. 72]. Це не зовсім так, а точніше, зовсім не так. В наведених формулах строк існує і він один і той же для двох еквівалентних ставок, тому він у формулах і не «виникає». Це формули для одного і того ж строку фінансової операції. Кількість періодів нарахування в цих формулах не змінюється, кількість n в мнжниках 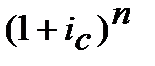 і
і 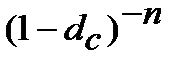 передбачається рівною, передбачається підсвідомо і тому автоматично скорочується за правилами математики. Строк і кількість періодів нарахування процентів ─ n присутні в будь-яких розрахунках де використовуються формули (8.17) та (8.18) і їх не явна присутність передбачає: ─ строк є, строк є і тому на розрахунок впливає, і цей строк не змінюється при заміні ставки на еквівалентну; ─ n в розрахунках присутня, n на розрахунки впливає тим, що n однакова для кожної еквівалентної ставки.Як тільки перейдемо до практичного застосування формул (8.17) та (8.18) відразу в розрахунках «виникають» і строк і кількість періодів нарахування і вони починають впливати на розрахунки. У випадках, коли n різні для ставок (
передбачається рівною, передбачається підсвідомо і тому автоматично скорочується за правилами математики. Строк і кількість періодів нарахування процентів ─ n присутні в будь-яких розрахунках де використовуються формули (8.17) та (8.18) і їх не явна присутність передбачає: ─ строк є, строк є і тому на розрахунок впливає, і цей строк не змінюється при заміні ставки на еквівалентну; ─ n в розрахунках присутня, n на розрахунки впливає тим, що n однакова для кожної еквівалентної ставки.Як тільки перейдемо до практичного застосування формул (8.17) та (8.18) відразу в розрахунках «виникають» і строк і кількість періодів нарахування і вони починають впливати на розрахунки. У випадках, коли n різні для ставок ( 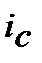 ) і(
) і( 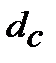 ), а їх еквівалентність треба розрахувати, формули еквівалентності будуть іншими, не схожими на (8.17) і (8.18), і в їх формалізованому записі будуть показники n відповідні своїм ставкам. Формули (8.17) і (8.18) ─ похідні формули від інших, більш загальних формул, в яких і строк і n фігурують у запису формули безпосередньо.
), а їх еквівалентність треба розрахувати, формули еквівалентності будуть іншими, не схожими на (8.17) і (8.18), і в їх формалізованому записі будуть показники n відповідні своїм ставкам. Формули (8.17) і (8.18) ─ похідні формули від інших, більш загальних формул, в яких і строк і n фігурують у запису формули безпосередньо.
Прикладом такого узагальнення може бути формула еквівалентності складної облікової ставки ( 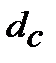 ) і номінальної складної процентної ставки(
) і номінальної складної процентної ставки( 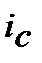 ) при нарахуванні процентів m разів у році, яку знайдемо з дорівнювання множників
) при нарахуванні процентів m разів у році, яку знайдемо з дорівнювання множників 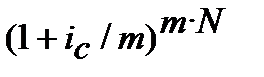 =
=  :
:
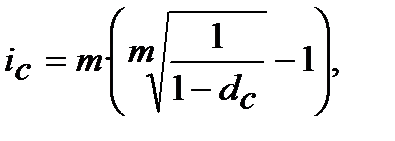 або
або 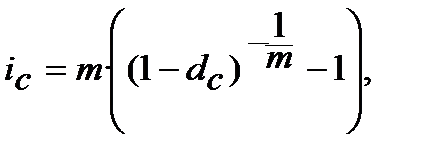 (8.19)
(8.19)
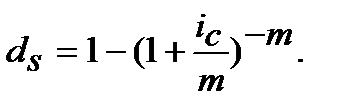 (8.20)
(8.20)
Еквівалентність складної облікової ставки ( 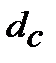 ) і простої облікової ставки
) і простої облікової ставки 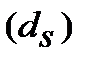 знайдемо з дорівнювання множників
знайдемо з дорівнювання множників 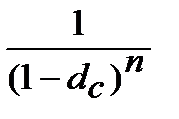 =
= 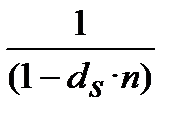 :
:
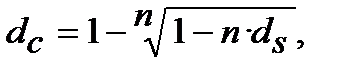 або
або 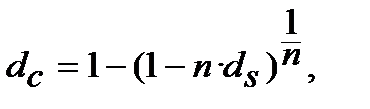 (8.21)
(8.21)
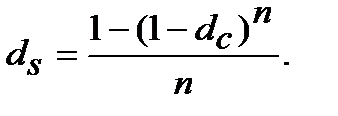 (8.22)
(8.22)
Якщо зафіксувати ставки тільки як номінальні, тобто ─ річні, то при застосуванні m та N формули (8.21) та (8.22) набувають такого вигляду:
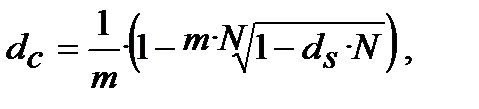 (8.23)
(8.23)
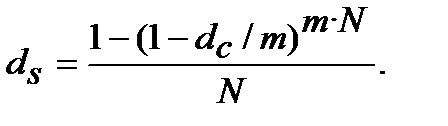 (8.24)
(8.24)
Еквівалентність простої процентної ставки (  ) і складної облікової ставки
) і складної облікової ставки 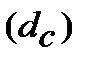 знайдемо з дорівнювання множників
знайдемо з дорівнювання множників  =
= 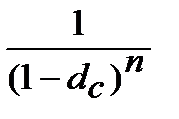 :
:
 (8.25)
(8.25)
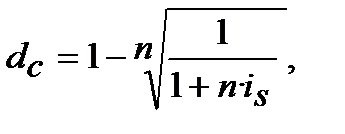 або
або 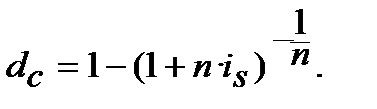 (8.26)
(8.26)
Якщо зафіксувати ставки тільки як номінальні, тобто ─ річні, то при застосуванні m та N формули (8.25) та (8.26) набувають такого вигляду:
 або
або 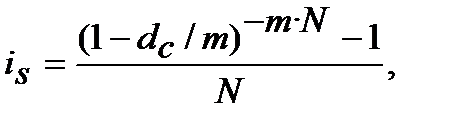 (8.27)
(8.27)
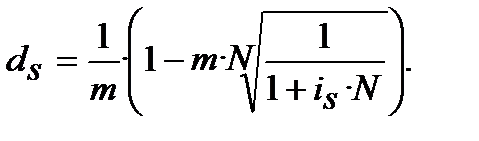 (8.28)
(8.28)
Таким чином розглянуто всі варіанти еквівалентності ставок, передбачених квадратом еквівалентності (рис. 8.1). Проголошувалось, що формул еквівалентності всього дванадцять, а у нас ─ вже 28. І все ж таки, основних формул еквівалентності ставок ─ дванадцять, а всі інші ─ похідні від цих дванадцяти. Основними формулами еквівалентності ставок є формули: (8.1), (8.2), (8.9), (8.10), (8.13), (8.14), (8.17), (8.18), (8.21), (8.22), (8.25), (8.26). В тексті їх номери в дужках виділені жирними цифрами.
Крім використаних вище дискретних формул існують формули безперервного нарахування (див. підрозділ 6.3).
Еквівалентність сили росту і процентних ставок:
─ для простої процентної ставки з дорівнювання множників 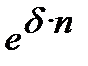 =
=  :
:
 (8.29)
(8.29)
 (8.30)
(8.30)
─ для складної процентної ставки з дорівнювання множників 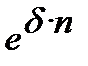 =
= 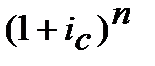 :
:
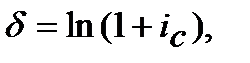 (8.31)
(8.31)
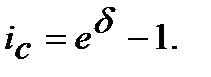 (8.32)
(8.32)
Еквівалентність сили росту і облікових ставок:
─ для простої облікової ставки з дорівнювання множників 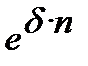 =
= 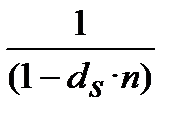 :
:
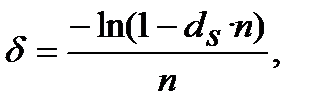 (8.33)
(8.33)
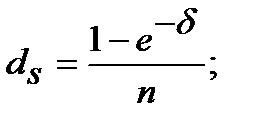 (8.34)
(8.34)
─ для складної облікової ставки з дорівнювання множників 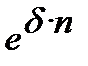 =
= 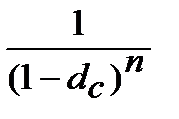 :
:
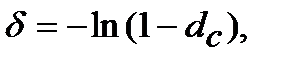 (8.35)
(8.35)
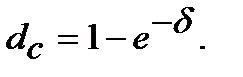 (8.36)
(8.36)
Еквівалентність сили росту і номінальної складної процентної ставкипри нарахуванні процентів m раз у роцірозраховується з порівнювання
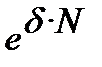 =
= 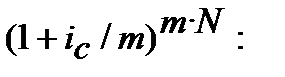
 (8.37)
(8.37)
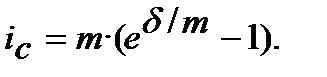 (8.38)
(8.38)
При лінійній зміні сили росту еквівалентну складну процентну ставку можна розрахувати за такою формулою:
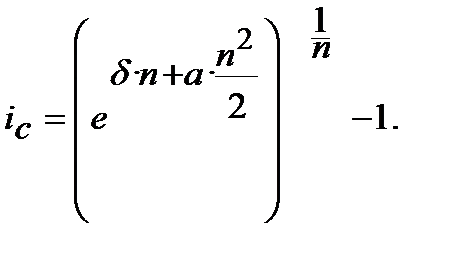 (8.39)
(8.39)
_Приклад 8.1___________________________________
Читайте також:
- Аварійно-рятувальні підрозділи Оперативно-рятувальної служби цивільного захисту, їх призначення і склад.
- Актив і пасив балансу складаються також з певних розділів.
- Активи, що реалізуються повільно (А3) – це статті 2-го розділу активу балансу, які включають запаси та інші оборотні активи (рядки 100 до 140 включно, а також рядок 250).
- Аналіз бойових дій пожежних підрозділів
- Б – розділення гелю на дві фази
- БАГАТОСТАНЦІЙНИЙ ДОСТУП І МЕТОДИ РОЗДІЛЕННЯ СИГНАЛІВ ЗЕМНИХ СТАНЦІЙ
- Баланс процентних ставок
- Банк даних про випадки порушень статутних правил взаємовідносин у військовому підрозділі
- Безпека ланцюгів поставок матеріальних ресурсів
- Взаємодія органів слідства з підрозділами, уповноваженими здійснювати оперативно-розшукову діяльність, при розслідуванні злочинів
- Взаємодія підрозділів при проведенні виїзних планових та позапланових перевірок
- Взаємодія СВА з іншими структурними підрозділами підприємства.
| <== попередня сторінка | | | наступна сторінка ==> |
| СТИСЛО ПРО ГОЛОВНЕ В РОЗДІЛІ 7 | | | Задача. |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |