
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Площа криволінійної трапеції
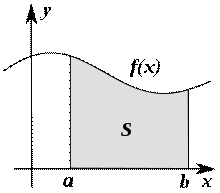 Криволінійною трапецієюназивається фігура, обмежена графіком неперервної функції
Криволінійною трапецієюназивається фігура, обмежена графіком неперервної функції  , яка невід’ємна на відрізку
, яка невід’ємна на відрізку 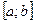 , прямими
, прямими  ,
, 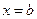 і віссю ОХ.
і віссю ОХ.
Площа криволінійної трапеції дорівнює визначеному інтегралу від заданої функції на заданому відрізку: 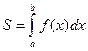 .
.
157.Побудувати схематично фігури, площі яких виражаються такими інтегралами:
1)  ; 2)
; 2) 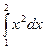 ;
;
3) 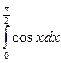 ; 4)
; 4) 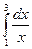 .
.
158.Записати за допомогою інтегралу площі фігур, зображених на рисунку:1)

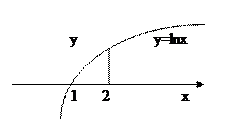
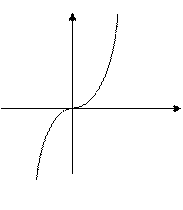
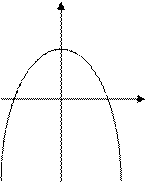
159.Знайти площу фігури, обмежену:
1) параболою 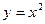 та прямими
та прямими  ,
, 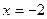 ,
, 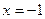 ;
;
2) параболою 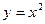 та прямими
та прямими  ,
, 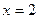 ,
, 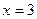 ;
;
3) графіком функції 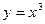 та прямими
та прямими  ,
, 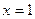 ;
;
4) графіком функції 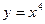 та прямими
та прямими  ,
, 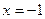 ;
;
5) графіком функції 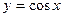 та прямими
та прямими  ,
, 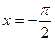 ,
, 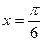 ;
;
6) графіком функції 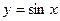 та прямими
та прямими  ,
, 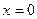 ,
, 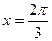 ;
;
7) параболою 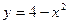 та віссю абсцис;
та віссю абсцис;
8) параболою 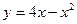 та віссю абсцис;
та віссю абсцис;
9) параболою 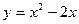 , віссю абсцис та прямою
, віссю абсцис та прямою 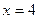 ;
;
10) параболою 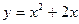 , віссю абсцис та прямою
, віссю абсцис та прямою  ;
;
11) графіком функції 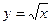 та прямими
та прямими  ,
, 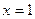 ,
, 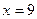 ;
;
12) графіком функції 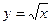 та прямими
та прямими  ,
, 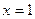 ,
, 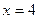 ;
;
13) графіком функції 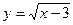 та прямими
та прямими  ,
, 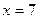 ;
;
14) графіком функції 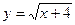 та прямими
та прямими  ,
, 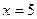 ;
;
15) графіком функції 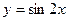 та прямими
та прямими  ,
, 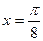 ,
, 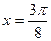 ;
;
16) графіком функції  та прямими
та прямими  ,
, 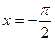 ,
, 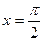 ;
;
17) графіком функції 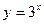 та прямими
та прямими  ,
, 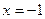 ,
, 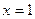 ;
;
18) графіком функції 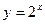 та прямими
та прямими  ,
, 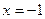 ,
, 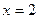 ;
;
19) графіком функції 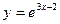 та прямими
та прямими  ,
, 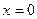 ,
, 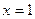 ;
;
20) графіком функції 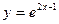 та прямими
та прямими  ,
, 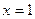 ,
, 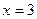 ;
;
21) графіком функції 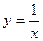 та прямими
та прямими  ,
, 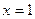 ,
, 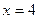 ;
;
22) графіком функції 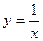 та прямими
та прямими  ,
, 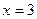 ,
,  ;
;
23) графіками рівнянь 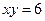 ,
, 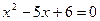 та
та  ;
;
24) графіками рівнянь 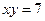 ,
, 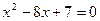 та
та  ;
;
160.Знайти площу фігури, обмежену:
1) параболою 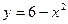 та прямою
та прямою 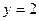 ;
;
2)параболою 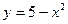 та прямою
та прямою  ;
;
3) параболою 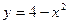 та прямою
та прямою 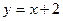 ;
;
4) параболою 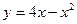 та прямою
та прямою 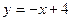 ;
;
5) параболою 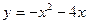 , прямою
, прямою  та віссю ординат;
та віссю ординат;
6) параболою 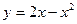 , прямою
, прямою 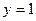 та віссю ординат;
та віссю ординат;
7) параболою 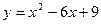 та прямою
та прямою 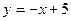 ;
;
8) параболою 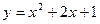 та прямою
та прямою 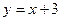 ;
;
9) графіком функції 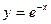 та прямими
та прямими 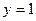 ,
,  ;
;
10) графіком функції 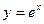 та прямими
та прямими 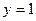 ,
, 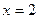 ;
;
11) графіком функції 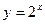 та прямими
та прямими 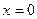 ,
,  ;
;
12) графіком функції 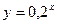 та прямими
та прямими 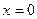 ,
, 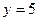 ;
;
13) графіком функції 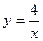 та прямими
та прямими 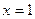 ,
, 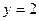 ;
;
14) графіком функції  та прямими
та прямими 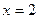 ,
,  ;
;
15) графіком функції  та прямими,
та прямими, 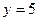 ,
, 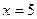 ;
;
16) графіком функції 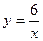 та прямими,
та прямими, 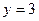 ,
, 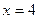 ;
;
17) графіком функції 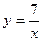 та прямою
та прямою 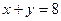 ;
;
18) графіком функції  та прямою
та прямою 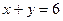 ;
;
19) графіком функції 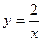 та прямими
та прямими 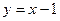 ,
, 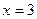 ;
;
20)графіком функції 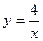 та прямими
та прямими 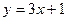 ,
, 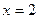 ;
;
21) графіками функцій 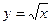 та
та 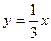 ;
;
22)графіками функцій 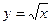 та
та  ;
;
23) параболою 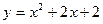 та прямою
та прямою 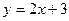 ;
;
24) параболою 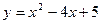 та прямою
та прямою 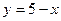 ;
;
25) параболами 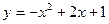 та
та 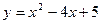 ;
;
26) параболами 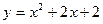 та
та 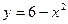 ;
;
27) графіками функцій  ,
, 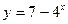 та прямою
та прямою 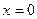 ;
;
28) графіками функцій 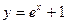 ,
, 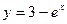 та прямою
та прямою 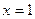 ;
;
29) графіками функцій 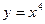 ,
, 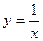 та прямою
та прямою 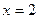 ;
;
30) графіками функцій 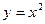 ,
, 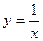 та прямою
та прямою 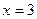 ;
;
31) графіками функцій 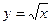 ,
, 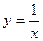 та прямою
та прямою 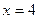 ;
;
32) графіками функцій 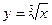 ,
, 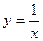 та прямою
та прямою 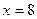 ;
;
33) графіком функції 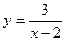 та прямими
та прямими 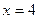 ,
,  ;
;
34) графіком функції  та прямими
та прямими 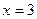 ,
, 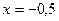 ;
;
35) графіками функцій 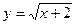 та
та 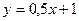 ;
;
36) графіками функцій 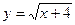 та
та 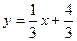 .
.
161.Знайти площі фігур, обмежені:
1) графіками функцій 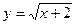 ,
, 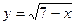 і віссю абсцис;
і віссю абсцис;
2) графіками функцій 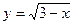 ,
, 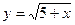 і віссю абсцис;
і віссю абсцис;
3) графіком функції 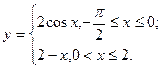 і віссю абсцис;
і віссю абсцис;
4) графіком функції 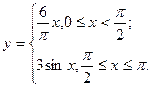 і віссю абсцис;
і віссю абсцис;
5) графіками функцій 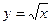 ,
, 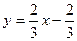 та віссю абсцис;
та віссю абсцис;
6) графіками функцій 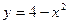 ,
, 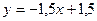 та віссю абсцис.
та віссю абсцис.
162.Використовуючи геометричний зміст інтегралу, обчислити:
1) 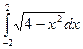 ; 2)
; 2) 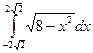 ;
;
3) 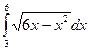 ; 4)
; 4) 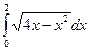 ;
;
5) 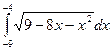 ; 6)
; 6) 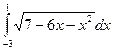 .
.
163.Знайти площу фігури, обмеженої параболою 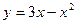 , дотичною, проведеною до цієї параболи в точці з абсцисою
, дотичною, проведеною до цієї параболи в точці з абсцисою  , та віссю ординат.
, та віссю ординат.
164.Знайти, при якому значенні 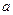 площа фігури, обмеженої параболою
площа фігури, обмеженої параболою 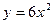 та прямими
та прямими  ,
,  ,
, 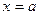 буде приймати найменше значення.
буде приймати найменше значення.
165.Знайти площу фігури, обмежену графіками функцій 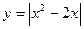 та
та 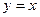 .
.
Читайте також:
- Адміністративний поділ, площа і населення українських земель у складі Речі Посполитої в першій воловині ХVІІ ст.
- Вибір площадки для будівництва.
- Виведення формул для знаходження площі паралелограма, трикутника, трапеції. Формули для знаходження площ поверхонь просторових геометричних фігур.
- Головні напруження та головні площадки.
- Головні площадки і головні напруження
- Забезпечення прийому парашутистів на площадці приземлення
- Забудова промислової площадки може бути суцільною або окремо розмі1
- Загальний центр ваги, площа опори й рівновага тіла
- Місце знаходження та площапідприємства.
- На площадці приземлення військової частини А1111
- Напруження на похилих площадках. Умови на поверхні.
- Обслуговування котлів, параметри площадок і сходів, для обслугову1
| <== попередня сторінка | | | наступна сторінка ==> |
| Визначений інтеграл та його властивості | | | Застосування визначеного інтеграла при розв’язанні фізичних задач |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |