• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Криві другого порядку

Рис. 3.52

Розділ 3. Аналітична геометрія

Аналітична геометрія є розділом вищої математики, в якому геометричні образи (точки, лінії, поверхні) вивчаються за допомогою алгебраїчних методів.

Засновником аналітичної геометрії вважають французького математика і філософа Декарта (1596–1650). Ним був розроблений і вперше застосований метод координат, який дав можливість пов’язати одне з одним геометричні та алгебраїчні поняття. Будь-якій лінії (чи поверхні) відповідає її рівняння, а потім властивості лінії (поверхні) вивчаються за допомогою аналітичного дослідження відповідного рівняння.

Криві другого порядку

1. Загальне рівняння кривої другого порядку. Рівняння другого степеня з двома змінними визначає на площині криву другого порядку, і до того ж єдину.

Таке рівняння має вигляд

.

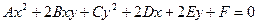В цьому рівнянні коефіцієнти можуть приймати дійсні значення за умови, що коефіцієнти 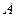, 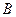і 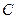одночасно не дорівнюють нулеві (так як у противному разі рівняння не буде рівнянням другого степеня).

Найбільш важливими з кривих другого порядку є еліпс (частинним випадком якого є коло), парабола і гіпербола; тому іноді тільки їх називають кривими другого порядку. Ці криві завжди викликали глибоке зацікавлення у вчених та інженерів і знаходили багаточисельне використання в науці та техніці. Про деякі з них ми будемо розмовляти під час вивчення теми.

Для того, щоб за умовою задачі скласти рівняння кривої, заданої множиною точок на площині, потрібно встановити залежність між координатами і 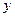довільної точки, яка належить цій множині, і параметрами (постійними величинами, заданими в умові задачі) і записати цю залежність у вигляді рівняння.

2.Коло і його рівняння. Вивчення кривих другого порядку почнемо з кола, однієї з найвідоміших ліній, які часто зустрічаються.

Прикладом кола є траєкторія руху матеріальної точки 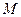, що рівномірно обертається на нитці, яка не розтягується, навколо нерухомого центра 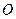(рис.3.1). В будь-який момент часу точка 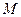віддалена від точки 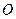на одну і ту саму відстань, рівну довжині нитки.

Колом називається множина всіх точок площини, рівновіддалених від однієї точки, яка називається центром.

Нехай центром кола є точка , а відстань до будь-якої точки 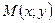кола дорівнює . Тоді, згідно формули відстані між двома точками, маємо .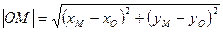

Підставимо в цей вираз координати точок 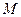і 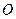та відстань , отримаємо , звідки після піднесення до квадрата знаходимо (1).

Рівняння (1) називають рівнянням кола з центром в точці 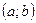і радіусом .

В тому випадку, коли центр кола співпадає з початком координат, отримаємо рівняння (2).

Рівняння (2) називається канонічним рівнянням кола.

Приклад 1. Скласти рівняння кола з центром і радіусом .

Розв’язання. За умовою 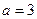, , . Підставимо , 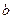і у рівняння (1), тоді .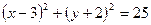

Відповідь: .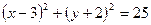

Приклад 2. Тіло, що рухається по колу , відірвалося від нього, знаходячись у точці 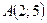. Визначити подальшу траєкторію тіла.

Розв’язання. Після відриву тіло буде рухатись по дотичній до даного кола, проведеної в точці 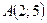. Як відомо, дотична перпендикулярна радіусу 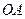, проведеному в точку дотику 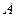. Центром кола є точка . З цього видно, що пряма 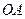паралельна осі ординат, а отже, дотична в точці 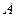паралельна осі абсцис і має рівняння 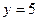. Отже, тіло буде рухатися по прямій .

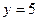Відповідь: тіло буде рухатися по прямій .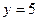

Контрольні питання

1) Записати загальне рівняння кривої другого порядку.

2) Як криві другого порядку є найбільш важливими?

3) Що називають колом?

4) Записати рівнянням кола з центром в точці 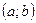і радіусом .

5) Записати канонічне рівняння кола.

Читайте також:

1. RLC-фільтр четвертого порядку
2. Автоматизовані станції управління насосними станціями водопостачання першого, другого і третього підйомів
3. Аспекти організаційного порядку
4. Афінний шифр k-ro порядку.
5. Бінарне відношення порядку.
6. Вестфальский мир як основа європейського правопорядку 1648-1815 рр.
7. Вибір індикатора . Криві титрування
8. Визначення порядку черги фаз трифазної системи
9. Визначники n-го порядку
10. Вища нервова діяльність у період другого дитинства
11. Відбулися кардинальні зміни у світовому порядку. На авансцену виходить Європа1.
12. Відношення еквівалентності та порядку, їх властивості. Впорядковані множини. Зв'язок відношення еквівалентності з розбиттям множини на класи, що попарно не перетинаються.

Переглядів: 2567