
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Поверхні другого порядку
1. Поняття поверхні другого порядку. Поверхнею, що визначається рівнянням 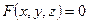 , називають сукупність всіх точок
, називають сукупність всіх точок 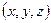 , координати яких задовольняють цьому рівнянню.
, координати яких задовольняють цьому рівнянню.
Поверхнями другого порядку називають поверхні, які в декартовій системі координат зображаються алгебраїчними рівняннями другого степеня, тобто рівняннями виду
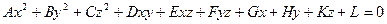 , (1)
, (1)
де 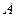 ,
, 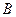 , …,
, …, 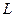 – дійсні числа, причому хоча б один з коефіцієнтів
– дійсні числа, причому хоча б один з коефіцієнтів 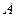 ,
, 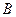 ,
, 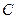 ,
, 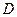 ,
,  ,
, 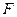 відмінний від нуля.
відмінний від нуля.
Рівняння (1) називають загальним рівнянням поверхні другого порядку.
Отже, поверхня другого порядку – це множина точок простору, координати яких задовольняють рівнянню 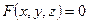 , де
, де  – многочлен другого степеня.
– многочлен другого степеня.
Розглянемо найпростіші (канонічні) рівняння поверхонь другого порядку і з’ясуємо питання про їх форму.
2. Циліндри другого порядку. Рівняння, яке не містить однієї з координат, зображає нескінчену циліндричну поверхню.
 Нехай рівняння
Нехай рівняння 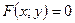 (1) не містить координати
(1) не містить координати  . Дане рівняння на площині
. Дане рівняння на площині 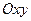 зображає деяку лінію
зображає деяку лінію 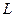 (рис.3.26).
(рис.3.26).
Якщо через точки цієї лінії проведемо прямі, паралельні осі  , то про будь-яку точку кожної з цих прямих можна сказати, що її координати
, то про будь-яку точку кожної з цих прямих можна сказати, що її координати  задоволь-няють рівняння (1), тому що довільна апліката цієї точки в рівняння (1) не входить.
задоволь-няють рівняння (1), тому що довільна апліката цієї точки в рівняння (1) не входить.
Отже, рівняння (1) задовольняють всі точки прямих, паралельних осі  , що проходять через точки деякої лінії
, що проходять через точки деякої лінії 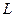 в площині
в площині 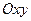 ; поверхня, утворена паралельними між собою прямими, що проходять через деяку «напрямну» лінію
; поверхня, утворена паралельними між собою прямими, що проходять через деяку «напрямну» лінію 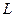 , називається циліндричної поверхнею; прямі, які її описують, називаються твірними.
, називається циліндричної поверхнею; прямі, які її описують, називаються твірними.
Отже, рівняння (1) зображає циліндричну поверхню, твірні якої паралельні осі  .
.
Відповідно рівняння 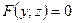 або
або  зображають циліндричні поверхні, причому твірні першої паралельні осі
зображають циліндричні поверхні, причому твірні першої паралельні осі  , твірні другої паралельні осі
, твірні другої паралельні осі  .
.
Циліндричною поверхнею, або циліндром, називається поверхня, утворена рухом прямої, яка перетинає задану криву і залишається паралельною сталому вектору.
Пряма, що своїм рухом утворює циліндр, називається його твірною, а крива, яку перетинають твірні – напрямною циліндра.
Циліндрами другого порядку називаються циліндричні поверхні, напрямними яких є лінії другого порядку.
Серед циліндричних поверхонь другого порядку розглянемо рівняння циліндрів з твірними, паралельними осі  . Їх рівняння, як вже було вказано раніше, не містять координати
. Їх рівняння, як вже було вказано раніше, не містять координати  .
.
Якщо за напрямну лінію в площині  взяти одну з кривих другого порядку
взяти одну з кривих другого порядку
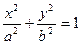 , (2)
, (2)  , (3)
, (3) 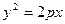 , (4)
, (4)
то кожне з цих рівнянь, якщо їх віднести до просторової системи координат, зображатиме циліндр другого порядку з твірними, паралельними осі  .
.
Рівняння (2) буде зображати циліндр, перерізи якого площинами, перпендикулярними твірним (паралельними площині 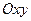 ), будуть еліпси з півосями
), будуть еліпси з півосями  і
і 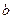 ; такий циліндри називається еліптичним (рис.3.27,а).
; такий циліндри називається еліптичним (рис.3.27,а).
Рівняння (3) буде зображувати циліндр, у якому плоскі перерізи, що перпендикулярні твірним, будуть гіперболами; його називають гіперболічним циліндром (рис.3.27,б).
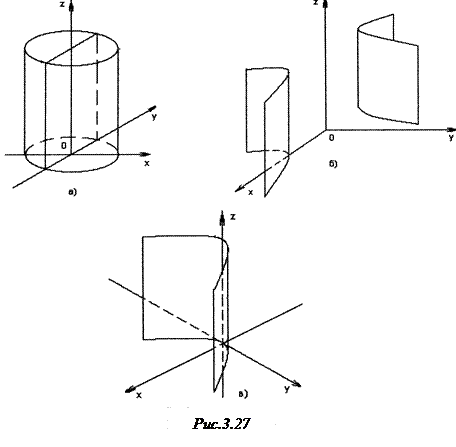
Рівняння (4) зображає циліндр з перпендикулярними до твірних плоскими перерізами у вигляді парабол; такий циліндр будемо називати параболічним (рис.3.27,в).
Приклад. Визначити вигляд поверхні 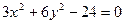 .
.
Розв’язання. Дане рівняння приводимо до вигляду  ;
;  .
.
Це рівняння в просторі визначає еліптичну циліндричну поверхню з напрямною в площині 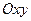 і твірними паралельними вісі
і твірними паралельними вісі  .
.
Відповідь: еліптичний циліндр.
3. Конус другого порядку. Сукупність всіх прямих, що проходять через кожну точку даної кривої 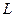 і деяку фіксовану точку
і деяку фіксовану точку 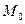 простору, що не лежить на цій кривій, називається конічною поверхнею.
простору, що не лежить на цій кривій, називається конічною поверхнею.
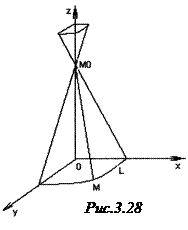 Дана крива
Дана крива  називається напрямною, дана фіксована точка
називається напрямною, дана фіксована точка  – вершиною, а прямі – твірними конічної поверхні (рис.3.28).
– вершиною, а прямі – твірними конічної поверхні (рис.3.28).
Конічні поверхні складаються з двох порожнин із спільною вершиною.
 Конічні і циліндричні поверхні мають особливу властивість: всі вони розгортаються на площині без складок і розривів, і , навпаки, з плоских листів матеріалу, зігнувши їх, можна отримати поверхні конічної і циліндричної форми. Дякуючи цій властивості вони отримали широке використання у техніці.
Конічні і циліндричні поверхні мають особливу властивість: всі вони розгортаються на площині без складок і розривів, і , навпаки, з плоских листів матеріалу, зігнувши їх, можна отримати поверхні конічної і циліндричної форми. Дякуючи цій властивості вони отримали широке використання у техніці.
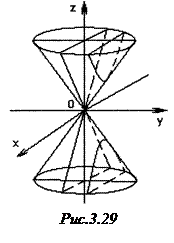
Конусом другого порядку називається поверхня, яка в прямокутній системі координат задається рівнянням
 . (1)
. (1)
Рівняння (1) називається канонічним рівнянням конуса.
Конус (1) утворюється прямими, які проходять через початок координат (рис.3.29).
Розглянемо перетини конуса площинами, паралельними координатним площинам.
Перетин площиною  зображається рівнянням
зображається рівнянням 
Перше з цих рівнянь зображає еліптичний циліндр, друге – площину паралельну площині 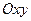 . Отже, перерізами конуса площинами
. Отже, перерізами конуса площинами  є еліпси з півосями
є еліпси з півосями  і
і  .
.
Зауважимо, що еліпс, який отримуємо при перетині конуса площиною  , вироджується в точку.
, вироджується в точку.
Лінії перерізу конуса площинами  чи
чи  є гіперболами, які вироджуються в пару прямих, якщо
є гіперболами, які вироджуються в пару прямих, якщо 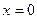 чи
чи 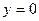 .
.
Приклад. Вісь  є віссю кругового конуса з вершиною в початку координат, точка
є віссю кругового конуса з вершиною в початку координат, точка 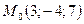 лежить на його поверхні. Скласти рівняння цього конуса.
лежить на його поверхні. Скласти рівняння цього конуса.
Розв’язання. Оскільки вісь  є віссю кругового конуса, то його рівняння шукаємо у вигляді
є віссю кругового конуса, то його рівняння шукаємо у вигляді  (бо площина
(бо площина  перетинає конус по колу, тобто
перетинає конус по колу, тобто 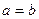 ). Точка
). Точка 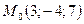 лежить на поверхні конуса. Тому її координати задовольняють рівняння конуса, тобто
лежить на поверхні конуса. Тому її координати задовольняють рівняння конуса, тобто  ,
,  ,
, 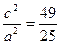 .
.
Отже, шукане рівняння конуса має вигляд  .
.
Відповідь:  .
.
4. Еліпсоїд. Еліпсоїдом називається поверхня, яка в декартовій прямокутній системі координат визначається рівнянням  (1), де
(1), де  ,
, 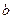 ,
, 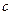 – додатні числа, що називаються півосями еліпсоїда (будемо вважати, що
– додатні числа, що називаються півосями еліпсоїда (будемо вважати, що  ).
).
Рівняння (1) називається канонічним рівнянням еліпсоїда.
Дослідимо форму еліпсоїда за його канонічним рівнянням:
1) Еліпсоїд не проходить через початок координат, так як точка  не задовольняє рівняння (1).
не задовольняє рівняння (1).
2) Точки перетину еліпсоїда з осями  :
:  і
і  ;
;  :
:  і
і  ;
;  :
: 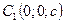 і
і 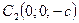 .
.
Еліпсоїд з кожною віссю координат перетинається у двох точках, симетричних відносно початку координат. Точки 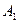 ,
, 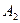 ,
,  ,
, 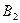 ,
,  і
і 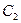 називаються вершинами, а відрізки
називаються вершинами, а відрізки 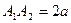 ,
, 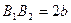 і
і  – осями еліпсоїда.
– осями еліпсоїда.
Якщо всі ці числа попарно різні, то еліпсоїд називається тривісним.
Якщо дві піввісі рівні одна одній, то отримаємо еліпсоїд обертання.
Якщо ж  , то поверхня представляє собою сферу з центром в початку координат.
, то поверхня представляє собою сферу з центром в початку координат.
3) Так як змінні  ,
, 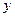 ,
,  містяться в рівнянні (1) тільки у парних степенях, то еліпсоїд симетричний відносно всіх координатних площин, координатних осей і початку координат, які називаються відповідно площинами симетрії, осями симетрії і центром симетрії еліпсоїда.
містяться в рівнянні (1) тільки у парних степенях, то еліпсоїд симетричний відносно всіх координатних площин, координатних осей і початку координат, які називаються відповідно площинами симетрії, осями симетрії і центром симетрії еліпсоїда.
4) Оскільки сума трьох додатних доданків лівої частини рівняння (1) дорівнює одиниці, то кожен з них (при дійсних значеннях координат) не може бути більшим від одиниці: 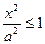 ,
, 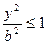 ,
,  .
.
Звідси випливає, що координати точок еліпсоїда задовольняють нерівності: 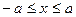 ,
,  ,
, 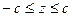 .
.
 Отже, еліпсоїд – це скінчена поверхня, яка повністю лежить в середині паралелепіпеда, розміри якого відповідно дорівнюють
Отже, еліпсоїд – це скінчена поверхня, яка повністю лежить в середині паралелепіпеда, розміри якого відповідно дорівнюють 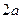 ,
, 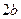 ,
,  .
.
Щоб уявити собі форму еліпсоїда і зобразити його на рисунку, використаємо метод паралельних перетинів.
Розглянемо перетин еліп-соїда будь-якою горизонталь-ною площиною  . Лінія, яку отримаємо при даному перетині, визначається рівняннями
. Лінія, яку отримаємо при даному перетині, визначається рівняннями  Звідси видно, перетин є еліпсом з півосями
Звідси видно, перетин є еліпсом з півосями 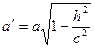 ,
, 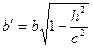 .
.
Аналогічну картину дістанемо і при перетині еліпсоїда площинами, паралельними кожній із двох інших його площин симетрії.
Лінії перетину еліпсоїда (1) є координатними площинами 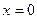 ,
, 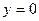 і
і  називаються головними перетинами еліпсоїда.
називаються головними перетинами еліпсоїда.
Еліпсоїд зображено на рис.3.30.
Приклад. Знайти півосі еліпса, утвореного при перетині еліпсоїда  площиною
площиною  .
.
Розв’язання. В рівняння еліпсоїда підставимо  . Отримаємо:
. Отримаємо:  ,
,  ,
,  ,
,  .
.
Отже, рівняння еліпса має вигляд 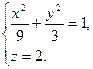
Тому півосі дорівнюють 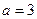 ,
, 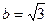 .
.
Відповідь: 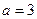 ,
, 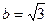 .
.
5. Однопорожнинний гіперболоїд. Однопорожнинний гіперболоїд – це поверхня, яка відносно деякої прямокутної декартової системи координат зображується рівнянням  (1), де
(1), де  ,
,  ,
, 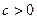 – числові параметри.
– числові параметри.
Рівняння (1) називається канонічним рівнянням однопорожнинного гіперболоїда.
Розглянемо його властивості:
1) Однопорожнинний гіперболоїд не проходить через початок координат, так як точка  не задовольняє рівняння (1).
не задовольняє рівняння (1).
2) Точки перетину гіперболоїда з осями  :
:  і
і  ;
;  :
:  і
і  ;
;  : в двох комплексно спряжених точках
: в двох комплексно спряжених точках  і
і 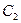 .
.
Вісь  не має з (1) спільних дійсних точок.
не має з (1) спільних дійсних точок.
Точки 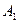 ,
, 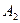 ,
,  і
і 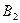 називаються вершинами гіперболоїда, а відрізки
називаються вершинами гіперболоїда, а відрізки 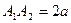 ,
, 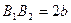 – дійсними осями,
– дійсними осями,  – уявною віссю. Числа
– уявною віссю. Числа  ,
, 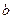 і
і 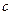 називаються півосями однопорожнинного гіперболоїда (1).
називаються півосями однопорожнинного гіперболоїда (1).
3) Однопорожнинний гіперболоїд симетричний відносно всіх координатних площин, координатних осей і початку координат, які називаються відповідно площинами симетрії, осями симетрії та центром симетрії.
4) Всі точки (1) розташовані поза асимптотичним конусом.
Вивчимо форму одно порожнинного гіперболоїда методом перерізів (рис.3.31).
 Площина
Площина 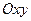 перетинає (1) по лінії, що має в цій площині рівняння
перетинає (1) по лінії, що має в цій площині рівняння 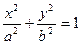 . Це – рівняння еліпса, який називається горловим еліпсом гіперболоїда.
. Це – рівняння еліпса, який називається горловим еліпсом гіперболоїда.
Площина  перетинає (1) по лінії, що має в цій площині рівняння
перетинає (1) по лінії, що має в цій площині рівняння 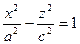 , а площина
, а площина 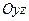 – по лінії, що має в цій площині рівняння
– по лінії, що має в цій площині рівняння  . Ці лінії називаються головними гіперболами однопорожнинного гіперболоїда.
. Ці лінії називаються головними гіперболами однопорожнинного гіперболоїда.
Перетини гіперболоїда площинами  є еліпсами
є еліпсами 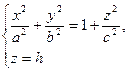 з півосями
з півосями  ,
,  .
.
Перетини площинами  і
і  є гіперболами (
є гіперболами ( 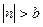 ,
,  ).
).
Приклад. Знайти лінію перетину однопорожнинного гіперболоїда 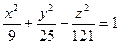 з площиною
з площиною 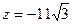 .
.
Розв’язання. В рівняння гіперболоїда підставимо 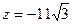 . Отримаємо:
. Отримаємо:  ,
, 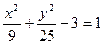 ,
,  ,
,  .
.
Отже, рівняння еліпса, що є лінією перетину однопорожнинного гіперболоїда, буде 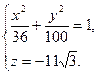
Відповідь: еліпс 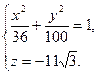
6. Двопорожнинний гіперболоїд. Двопорожнинним гіперболоїдом називається поверхня, яка в декартовій прямокутній системі координат визначається рівнянням 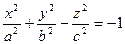 (1).
(1).
 Рівняння (1) називається канонічним рівнянням двопорожнинного гіпербол-лоїда.
Рівняння (1) називається канонічним рівнянням двопорожнинного гіпербол-лоїда.
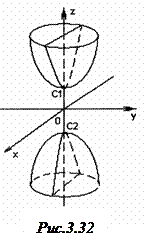
Розглянемо його властивості (рис.3.32):
1) Двопорожнинний гіперболоїд не проходить через початок координат, так як координати точки  не задовольняє рівняння (1).
не задовольняє рівняння (1).
2) Гіперболоїд перетинає вісь  в точках
в точках 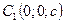 і
і 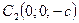 . Осі
. Осі  і
і  не перетинають гіперболоїд в дійсних точках.
не перетинають гіперболоїд в дійсних точках.
Точки  і
і 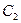 називаються вершинами гіперболоїда, відрізок
називаються вершинами гіперболоїда, відрізок  є дійсною віссю, а
є дійсною віссю, а 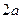 і
і 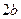 – уявними осями. Числа
– уявними осями. Числа  ,
, 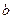 і
і 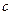 називаються півосями гіперболоїда.
називаються півосями гіперболоїда.
3) Гіперболоїд симетричний відносно всіх координатних площин (площини симетрії), координатних осей (осі симетрії) і початку координат (центр симетрії).
4) Множина точок, що лежать на асимптотах, які проходять через початок координат, є конусом, який визначається рівнянням 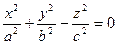 . Цей конус – асимптотичний конус з вершиною в початку координат.
. Цей конус – асимптотичний конус з вершиною в початку координат.
Всі точки гіперболоїда розташовані всередині асимптотичного конуса.
5) Гіперболоїд є центральною поверхнею з центром в початку координат.
6) Перерізи гіперболоїда площинами  (
(  ) представляють собою еліпси; перерізи площинами
) представляють собою еліпси; перерізи площинами  і
і  є гіперболами.
є гіперболами.
Приклад. Знайти головні перерізи поверхні  .
.
Розв’язання. Прийнявши в даному рівнянні  , одержимо рівняння лінії перетину з площиною
, одержимо рівняння лінії перетину з площиною 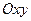
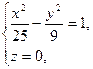 яке в площині
яке в площині 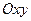 визначає гіперболу.
визначає гіперболу.
В перетині з площиною 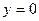 (
(  ) маємо гіперболу
) маємо гіперболу 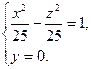
Площина 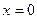 (
( 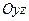 ) не перетинає отриманої поверхні, бо рівняння
) не перетинає отриманої поверхні, бо рівняння 
Відповідь: гіперболи 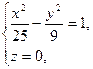 і
і 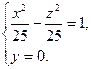
7. Еліптичний параболоїд. Еліптичним параболоїдом називається поверхня, яка в декартовій прямокутній системі координат визначається рівнянням 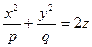 ,
,  ,
, 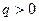 (1).
(1).
Рівняння (1) називається канонічним рівнянням еліптичного параболоїда.
Розглянемо його властивості (рис.3.33):
1)  Параболоїд проходить через початок координат, так як точка
Параболоїд проходить через початок координат, так як точка  задовольняє рівняння (1).
задовольняє рівняння (1).
2) Перетинає всі осі координат лише в одній точці  . Вона називається вершиною параболоїда.
. Вона називається вершиною параболоїда.
3) Координатні площини  і
і 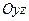 є площинами симетрії параболоїда. Координатна вісь
є площинами симетрії параболоїда. Координатна вісь  є віссю симетрії.
є віссю симетрії.
4) Вся поверхня розташована над площиною 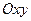 , оскільки якщо
, оскільки якщо  , рівняння (1) не може задовольнятись при жодних дійсних значеннях
, рівняння (1) не може задовольнятись при жодних дійсних значеннях  і
і 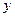 .
.
Визначимо форму параболоїда методом перерізів.
Якщо параболоїд перетнути площиною  , паралельною площині
, паралельною площині 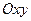 , то
, то


Отже, всі площини, паралельні 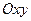 і відтинаючи від
і відтинаючи від  відрізки
відрізки  , перетинають параболоїд по еліпсам.
, перетинають параболоїд по еліпсам.
Площини, паралельні іншим координатним площинам, перетинають параболоїд по параболам.
Приклад. Знайти головні перерізи поверхні  та переріз площиною
та переріз площиною  .
.
Розв’язання. Приймемо 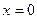 , одержимо рівняння лінії перетину з площиною
, одержимо рівняння лінії перетину з площиною 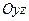 :
:

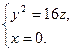
Отримали рівняння параболи.
Нехай 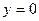 , одержимо рівняння лінії перетину з площиною
, одержимо рівняння лінії перетину з площиною  :
:
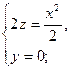

Отримали рівняння параболи.
Дослідимо переріз площиною  :
:


Отримали рівняння еліпса.
Відповідь: головні перерізи – параболи; переріз площиною  – еліпс.
– еліпс.
8. Гіперболічний параболоїд. Гіперболічним параболоїдом називається поверхня, яка в декартовій прямокутній системі координат визначається рівнянням 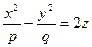 ,
,  ,
, 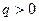 (1).
(1).
Рівняння (1) називається канонічним рівнянням гіперболічного параболоїда.
Розглянемо його властивості (рис.3.34):
1)  Гіперболічний параболоїд проходить через початок координат.
Гіперболічний параболоїд проходить через початок координат.
2) Параболоїд перетинається з осями координат в єдиній точці – в початку координат.
3) Параболоїд симетричний відносно площин  і
і 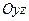 .
.
Визначимо форму гіперболічного параболоїда методом перерізів.
Площина  перетинає поверхню по лінії
перетинає поверхню по лінії


тобто по двох прямих 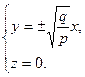
Площина  перетинає поверхню по гіперболі
перетинає поверхню по гіперболі 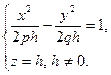
Якщо  , дійсною віссю цієї гіперболи буде паралель осі
, дійсною віссю цієї гіперболи буде паралель осі  ; якщо
; якщо  , дійсною віссю буде паралель осі
, дійсною віссю буде паралель осі  .
.
Розглянемо тепер переріз поверхні площинами  . Вони будуть зображатися рівняннями
. Вони будуть зображатися рівняннями 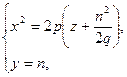 які визначають параболи з параметром
які визначають параболи з параметром 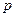 .
.
Якщо поверхні перетинати площинами  , то в перерізі отримаємо параболи
, то в перерізі отримаємо параболи 
Приклад. При перетині гіперболічного параболоїда площиною 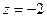 отримали гіперболу
отримали гіперболу  . Написати канонічне рівняння цього параболоїда.
. Написати канонічне рівняння цього параболоїда.
Розв’язання. Загальний вигляд гіперболи, по якій площина 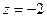 перетинає гіперболічний параболоїд
перетинає гіперболічний параболоїд 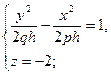 тоді
тоді 
Знайдемо 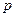 і
і 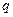 :
:  ,
,  ;
;  ,
, 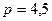 .
.
Загальний вигляд гіперболічного параболоїда 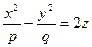 , тоді
, тоді 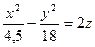 .
.
Відповідь: 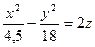 .
.
9. Поверхні обертання. Нехай в площині 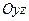 задана лінія
задана лінія 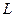 , рівняння якої має вигляд
, рівняння якої має вигляд  (1)
(1)
Знайдемо рівняння поверхні  , яка отримується при обертанні цієї лінії навколо осі
, яка отримується при обертанні цієї лінії навколо осі  (рис.3.35).
(рис.3.35).
 Візьмемо довільну точку
Візьмемо довільну точку 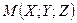 , яка лежить на поверхні
, яка лежить на поверхні  і проведемо через неї площину перпендикулярну до осі обертання
і проведемо через неї площину перпендикулярну до осі обертання  . У перетині маємо коло, центр якого лежить в точці
. У перетині маємо коло, центр якого лежить в точці 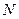 на осі обертання. Координати точки
на осі обертання. Координати точки  . Радіус кола
. Радіус кола  як відстань між двома точками
як відстань між двома точками 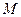 і
і 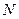 дорівнює
дорівнює  . З іншого боку, цей радіус є абсолютним значенням аплікати точки
. З іншого боку, цей радіус є абсолютним значенням аплікати точки 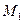 заданої лінії
заданої лінії 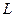 , а ордината цієї точки дорівнює
, а ордината цієї точки дорівнює 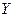 . Отже, прийнявши в рівнянні (1)
. Отже, прийнявши в рівнянні (1) 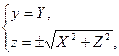 ми отримаємо шукане рівняння поверхні обертання
ми отримаємо шукане рівняння поверхні обертання  :
:  (2).
(2).
Отже, маємо правило для одержання рівняння поверхні обертання.
Для того щоб отримати рівняння поверхні, утвореної обертанням лінії 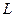 , що лежить в площині
, що лежить в площині 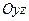 , навколо осі
, навколо осі  , потрібно в рівнянні цієї лінії замінити
, потрібно в рівнянні цієї лінії замінити  на
на 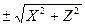 , а
, а 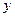 залишити без зміни.
залишити без зміни.
Аналогічні правила справедливі і щодо поверхонь, які отримуються обертанням плоских ліній навколо інших координатних осей.
1) Поверхня, яка отримується обертанням еліпса навколо однієї з його осей, називається еліпсоїдом обертання.
Нехай в площині 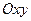 еліпс задано рівнянням
еліпс задано рівнянням 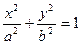 (3).
(3).
Складемо рівняння поверхні, отриманої обертанням його навколо осі  .
.
В рівнянні (3)  замінимо на
замінимо на  .
.
Після заміни отримаємо  (4).
(4).
Це рівняння зазвичай записують так  .
.
При 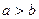 рівняння (4) визначає еліпсоїд обертання витягнутий вздовж осі
рівняння (4) визначає еліпсоїд обертання витягнутий вздовж осі  , при
, при  рівняння (4) визначає еліпсоїд обертання, стиснутий вздовж осі
рівняння (4) визначає еліпсоїд обертання, стиснутий вздовж осі  , а при
, а при 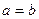 воно визначає сферу.
воно визначає сферу.
Приклад 1. Еліпс з півосями 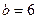 ,
,  і центром в початку координат обертається навколо своєї малої осі, співпадаючої з віссю
і центром в початку координат обертається навколо своєї малої осі, співпадаючої з віссю  . Скласти рівняння поверхні, яка описується еліпсом при його обертанні.
. Скласти рівняння поверхні, яка описується еліпсом при його обертанні.
Розв’язання. Складемо рівняння даного еліпса 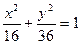 . Замінивши в цьому рівнянні
. Замінивши в цьому рівнянні  на
на  , отримаємо шукане рівняння еліпсоїда обертання
, отримаємо шукане рівняння еліпсоїда обертання 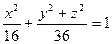 або
або 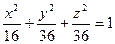 .
.
Відповідь: 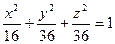 .
.
2) Поверхня, яка отримується обертанням гіперболи навколо однієї з її осей, називається гіперболоїдом обертання.
При обертанні гіперболи навколо її дійсної осі отримується двопорожнинний гіперболоїд обертання, а при обертанні гіперболи навколо її уявної осі отримується однопорожнинний гіперболоїд обертання.
Нехай в площині 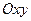 гіпербола задана рівнянням
гіпербола задана рівнянням  (5).
(5).
Складемо рівняння поверхні, отриманої обертанням гіперболи навколо її дійсної вісі  .
.
Для отримання рівняння поверхні двопорожнинного гіперболоїда обертання достатньо в рівнянні гіперболи (5)  замінимо на
замінимо на  .
.
Після заміни отримаємо  (6).
(6).
При обертанні гіперболи (5) навколо її уявної осі потрібно в рівнянні (5) 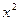 замінити на
замінити на  ; після заміни отримаємо
; після заміни отримаємо  (7).
(7).
Приклад 2. Гіпербола з півосями 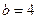 і
і 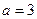 обертається навколо своєї уявної осі, співпадаючої з віссю
обертається навколо своєї уявної осі, співпадаючої з віссю  . Центр гіперболи співпадає з початком координат. Скласти рівняння поверхні, отриманої при обертанні цієї гіперболи.
. Центр гіперболи співпадає з початком координат. Скласти рівняння поверхні, отриманої при обертанні цієї гіперболи.
Розв’язання. Складемо рівняння гіперболи 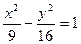 .
.
Щоб отримати рівняння гіперболоїда обертання, в рівнянні гіперболи 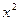 замінимо на
замінимо на  . Після заміни отримаємо
. Після заміни отримаємо 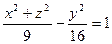 або
або  .
.
Відповідь:  .
.
3) Поверхня, яка отримується обертанням параболи навколо її осі симетрії, називається параболоїдом обертання.
Нехай на площині 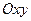 парабола задана рівнянням
парабола задана рівнянням 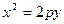 (8).
(8).
Для отримання рівняння поверхні обертання потрібно в рівнянні (8) 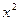 замінити на
замінити на  ; після заміни отримаємо
; після заміни отримаємо  (9).
(9).
Відмітимо одну особливу властивість цієї поверхні. Якщо внутрішню поверхню параболоїда обертання зробити дзеркальною, а в її фокусі (фокусом параболоїда обертання називається фокус параболи, що обертається) помістити джерело світла, то всі промені світла, відбиваючись від поверхні параболоїда, підуть паралельно осі параболоїда.
Ця властивість широко використовується при виготовленні світло відбиваючих пристроїв (прожекторів, фар автомобіля, інших пристроїв).
Приклад 3. Скласти рівняння поверхні, отриманої обертанням параболи 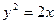 навколо осі
навколо осі  .
.
Розв’язання. Щоб скласти рівняння параболоїда обертання, отриманого обертанням параболи навколо осі  , потрібно в рівнянні
, потрібно в рівнянні 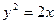 замінити
замінити  на
на  , після заміни отримаємо
, після заміни отримаємо  .
.
Відповідь:  .
.
4) Якщо обертати пряму, паралельну будь-якій осі координат, навколо цієї осі, то отримається кругова циліндрична поверхня.
Нехай дана пряма, що лежить в площині 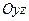 і має рівняння
і має рівняння  .
.
Поверхня обертання цієї прямої навколо осі  має рівняння
має рівняння  .
.
Приклад 4. Скласти рівняння циліндричної поверхні, отриманої обертанням прямої  , що лежить в площині
, що лежить в площині 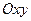 навколо осі
навколо осі  .
.
Розв’язання. В рівнянні  замінимо
замінимо  на
на  , в результаті отримаємо
, в результаті отримаємо  .
.
Відповідь:  .
.
5) Нехай дана пряма, що лежить в площині 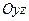 і проходить через початок координат,
і проходить через початок координат,  ,
,  .
.
Рівняння поверхні обертання цієї прямої навколо осі  має вигляд
має вигляд  .
.
Отримане рівняння є рівнянням шуканої поверхні обертання, яка називається круговою конічною поверхнею.
Приклад 5. Скласти рівняння поверхні обертання прямої  ,
,  навколо вісі
навколо вісі  .
.
Розв’язання. З рівняння  знаходимо
знаходимо  . Це і є шукане рівняння.
. Це і є шукане рівняння.
Відповідь:  .
.
Контрольні питання
1. Дати означення поверхні II порядку.
2. Записати рівняння поверхні II порядку.
3. Що називають циліндричною поверхнею?
4. Що таке циліндрична поверхня II порядку?
5. Що представляють собою еліптичний, гіперболічний і параболічний циліндри?
6. Що називають конічною поверхнею?
7. Що таке конус II порядку?
8. Які лінії утворюються в результаті перетину конуса площинами, паралельними координатним площинам?
9. Що називають еліпсоїдом?
10. Основні елементи еліпсоїда.
11. Що називають однопорожнинним гіперболоїдом?
12. Основні елементи однопорожнинного гіперболоїда.
13. Що називають двопорожнинним гіперболоїдом?
14. Основні елементи двопорожнинного гіперболоїда.
15. Що називають еліптичним параболоїдом?
16. Основні елементи еліптичного параболоїда.
17. Що називають гіперболічним параболоїдом?
18. Основні елементи гіперболічного параболоїда.
19. Що таке поверхня обертання? Як утворюють її рівняння?
20. Еліпсоїд, гіперболоїд та параболоїд обертання.
Читайте також:
- RLC-фільтр четвертого порядку
- Автоматизовані станції управління насосними станціями водопостачання першого, другого і третього підйомів
- Алгоритм розрахунку температури поверхні чипу ІМС процесора
- Аспекти організаційного порядку
- Афінний шифр k-ro порядку.
- Бінарне відношення порядку.
- Великої питомої поверхні пилинок (відношення площі поверхні до їх
- Вестфальский мир як основа європейського правопорядку 1648-1815 рр.
- Визначення порядку черги фаз трифазної системи
- Визначення температури на поверхні ізоляції принадземномупрокладанні та при прокладанні трубопроводів в приміщенні.
- Визначники n-го порядку
- Вимірювання розмірів деталей та шорсткуватості поверхні
| <== попередня сторінка | | | наступна сторінка ==> |
| Відповіді | | | Практичні завдання |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |