• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тема 1: Системи лінійних алгебраїчних рівнянь

Універсальність JK–тригера виявляється в тому, що, змінюючи зовнішню комутацію, його можна перетворити в будь–який інший тип тригера: RS, D, Т. Як RS–тригер він використовується за умови заборони комбінації J = К = 1. Для роботи як D–тригер вхід J через інвертор під’єднують до входу К (рис. 9.22, в)При цьому вхід J виконує функцію D–входу. Т–тригер отримують, коли з’єднані входи J та К в один лічильний вхід Т (рис. 9.22, г).

Тригери на цифрових елементах використовують в пристроях обробки й зберігання інформації. Крім поділу й лічби числа імпульсів, тригери широко використовують як елементи пам'яті EОМ, що запам'ятовують інформацію у вигляді двійкових чисел, які складаються з цифр 0 і 1; як пристрої для порівняння двох напруг (якщо до входу тригера подати змінний рівень напруги, то тригер спрацьовує й видає сигнал на виході після досягнення деякого порого­вого рівня напруги U_пор)та ін.

Тригери на цифрових інтегральних мікросхемах виконують як м класичною схемою на біполярних транзисторах, так і з використанням стандартних логіч­них елементів. У багатьох серіях мікросхем є інтегральні тригери, наприклад, RS–тригери–мікросхеми 115ТР1, 136ТР1; D–тригери – мікросхеми K131ТM2, 133ТМ2; JK–тригери – мікросхеми 130ТВ1, 133ТВ1 та ін.

Рис.1. Морфологические признаки недоношенности.

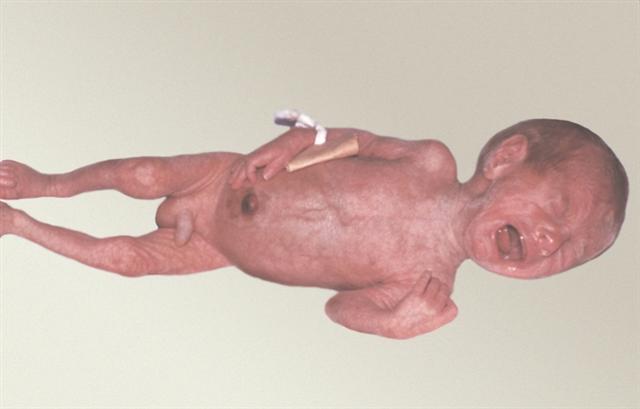
Рис.2. 4 степень недоношенности.

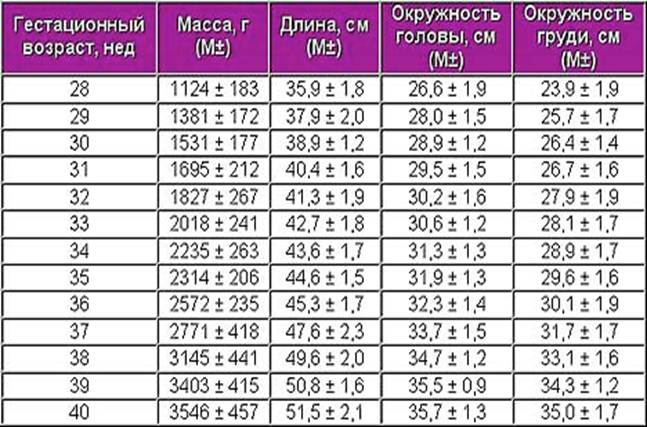
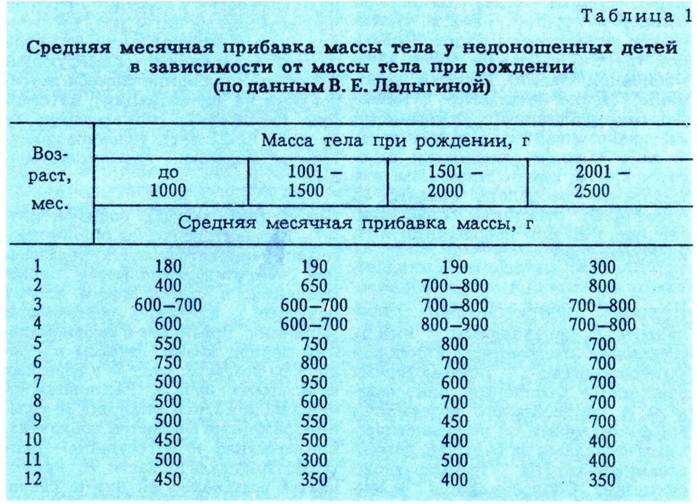
Таблица 2. Основные параметры физического развития новорожденных с учетом гестационного возраста.

Тема 1: Системи лінійних алгебраїчних рівнянь

§ 1.1. Поняття n-вимірного рядка та матриці

Означення 1.1.1. n-вимірним рядком називається упорядкована сукупність n дійсних чисел . Числа називають координатами рядка; – i-та координата рядка, .

Рядок з координатами будемо позначати так: . Рядок будемо називати нульовим.

Означення 1.1.2.Два рядки та називаються рівними, якщо їх вимірності та відповідні координати збігаються, тобто якщо та , .

Означення 1.1.3.Додавання двох n-вимірних рядків та множення n- вимірного рядка на дійсне число визначаються за правилами:

+ = ;

l = .

Приклад. Знайти суму двох рядків , та добуток першого рядка на число .

Розв’язання. За означенням 1.1.3 операції додавання рядків:

.

Згідно з означенням множення рядка на число:

.

Для стислості викладання будемо на подальшому n-вимірні рядки позначати латинськими буквами , а дійсні числа – грецькими буквами .

Операції додавання рядків та множення рядка на число мають такі властивості:

1) 2) 3)

4) 5) 6) ; 7) .

Тут – довільні n-вимірні рядки, – довільні дійсні числа, – нульовий рядок, .

Властивість 1) характеризується як «комутативність відносно додавання», а властивість 2) як «асоціативність відносно додавання».

Доведемо одну з цих властивостей, наприклад, 4.

4Нехай , , тоді:

/за означенням операції множення рядка на число/ /за властивістю дистрибутивності у множені дійсних чисел/ /за означенням операції додавання рядків/ /повертаючись до вихідних позначень/ .

Таким чином, для будь-яких рядків , та будь-якого числа має місце рівність .3

Введемо поняття матриці.

Означення 1.1.4. Матриця – це прямокутна таблиця, яка складається з n-вимірних рядків, що розташовані один під одним:

.

Числа називають елементами матриці та позначають маленькими латинськими буквами із двома індексами: перший – номер рядка, у якому розташовано елемент, другий – номер стовпця. Наведена вище матриця А містить m рядків та n стовпчиків. У цьому випадку кажуть, що вона є матрицею розміру . Будь-який рядок матриці А можна розглядати як матрицю розміром , а будь-який стовпчик – як матрицю розміру .

Приклад.Матриця має розмір , матриця – це матриця-рядок розміру , а матриця – це матриця-стовпчик розміру .

Матриця, усі елементи якої дорівнюють нулю, називається нульовою. Матрицю розміру називають квадратною матрицею порядку n. Квадратна матриця вигляду

називається одиничною.

Головною діагоналлю квадратної матриці називається діагональ проведена з лівого верхнього у правий нижній кут цієї матриці. Побічною діагоналлю квадратної матриці називається діагональ, що проведена з лівого нижнього у правий верхній кут матриці.

Означення 1.5. Східчастою матрицею називається матриця, яка задовольняє таким умовам:

· якщо який-небудь рядок матриці нульовий, то усі рядки, що розташовані після нього, також нульові;

· якщо перші ненульові елементи i-го та -го рядків (тобто двох сусідніх рядків) розташовані у стовпчиках з номерами та , то , тобто якщо розглядати два сусідні ненульові рядки, то перший ненульовий елемент у верхньому рядку зустрічається раніше, ніж у нижньому.

Приклад. З’ясувати, чи є східчастою матриця А:

.

Розв’язання. Ця матриця – східчаста, оскільки вона задовольняє усім умовам означення, а саме: та .

За домовленістю, до східчастих матриць будемо відносити нульову матрицю та матрицю, яка містить тільки один рядок.

Читайте також:

1. I. Органи і системи, що забезпечують функцію виділення
2. I. Особливості аферентних і еферентних шляхів вегетативного і соматичного відділів нервової системи
3. II. Анатомічний склад лімфатичної системи
4. II. Критерій найбільших лінійних деформацій
5. IV. Розподіл нервової системи
6. IV. Система зв’язків всередині центральної нервової системи
7. IV. Філогенез кровоносної системи
8. POS-системи
9. T. Сутність, етіологія та патогенез порушень опорно-рухової системи
10. VI. Філогенез нервової системи
11. А) Заробітна плата її форми та системи.
12. А) Заробітна плата, її форми та системи.

Переглядів: 1043