• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Теоретичні відомості

Перехідні або неустановлені процеси мають місце при переході від одного установленого стану електричного кола до другого і виникають при вмиканні, зміні напруги чи параметрів кола, короткому замиканні її елементів або інших змін.

Будь-які зміни в колі можна подати у вигляді тих чи інших перемикань, які будемо називати комутацією. Характер комутації на електричній схемі вказується за допомогою рубильника зі стрілкою (рис. 7.1), причому за напрямком стрілки можна судити замикається рубильник чи розмикається.

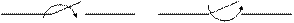
а б

Рис. 7.1. Характер комутації:

а – рубильник увімкнений; б – рубильник вимкнений

Передбачають, що комутація проходить при 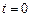. При чому перший момент до комутації позначається 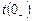, а перший момент після комутації .

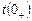Для аналізу перехідних процесів важливе значення мають два закони комутації.

За першим законом комутації струм в індуктивності не може змінюватися стрибкоподібно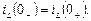

За другим законом комутації напруга на ємності не може змінюватися стрибкоподібно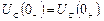

Перший та другий закони комутації витікають з того, що енергія, яка акумулювалася в реактивних елементах електричного кола 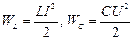не може змінюватися стрибкоподібно, інакше це означало б наявність нескінченної потужності.

Значення струмів в індуктивності та напруги на ємності в момент комутації називається початковими умовами.

Якщо струм в індуктивності та напруга на ємності в перший момент комутації дорівнюють нулю, то такі умови називаються нульовими початковими умовами.

Перехідні процеси в електричних колах описуються системами інтегрально-диференціальних рівнянь, які складаються на основі законів Кірхгофа для миттєвих значень струмів та напруг. В електротехніці для аналізу перехідних процесів широко застосовується класичний метод, що дозволяє спростити розгляд фізичних процесів.

Нехай в деякому електричному колі (рис. 7.2) раптово міняється опір. До комутації в колі існував опір 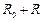, після комутації залишився опір тільки 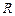. Вимагається дослідити перехідний струм і. Електричний стан схеми після комутації описується інтегрально-диференціальним рівнянням.

.

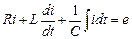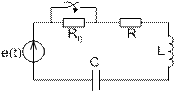
Рис. 7.2. Раптова зміна параметрів електричного кола

Якщо це рівняння продиференціювати за часом, то отримаємо диференціальне рівняння другого порядку, в якому як коефіцієнти виступають параметри кола чи їх комбінації.

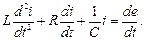
Як відомо з курсу математики загальний розв’язок лінійного неоднорідного диференціального рівняння дорівнює окремому розв’язку неоднорідного диференціального та загальному розв’язку однорідного диференціального рівняння. Окремий розв’язок неоднорідного диференціального рівняння знаходять з аналізу встановленого режиму після комутації. Тому цей режим називають примусовим режимом, а струми та напруги, знайдені в цьому режимі отримали назву примусових або встановлених.

Струми та напруги, знайдені при розв’язанні однорідних диференціальних рівнянь отримали назву вільних складників або вільних.

Однорідне диференціальне рівняння отримують із неоднорідного диференціального рівняння шляхом його звільнення від правої частини. Тоді для розглянутого кола однорідне диференціальне рівняння прийме вигляд

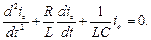
Розв’язок диференціального рівняння другого порядку записується в такому вигляді:

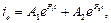
де 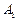і 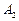– сталі інтегрування; 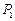і 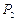– корені характеристичного рівняння. Характеристичне рівняння отримаємо шляхом алгебраїзації початкового диференціального рівняння

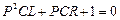
Дійсний (перехідний) струм дорівнює сумі примусової та вільної складових

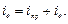
Розглянемо декілька прикладів перехідних процесів, які виникають при комутації при увімкненні електричного кола з реактивними елементами під напругу.

1. Нехай коло 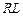під’єднується до постійної напруги 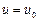(рис. 7.3). Складемо диференціальне рівняння кола після комутації на основі другого закону Кірхгофа

,

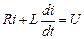тобто отримали неоднорідне рівняння першого порядку.

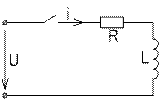
Рис. 7.3. Увімкнення кола 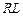до постійної напруги

Загальне рівняння отриманого диференціального рівняння, як відомо, буде

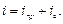
Примусова складова визначається як установлений струм в колі після закінчення перехідного процесу:

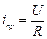
Вільна складова – загальний розв’язок однорідного диференціального рівняння:

.

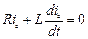Однорідне диференціальне рівняння першого порядку має своїм розв’язком вираз

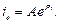
де 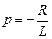– корінь характеристичного рівняння .

Таким чином загальний розв’язок неоднорідного диференціального рівняння має вигляд:

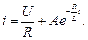
Для знаходження сталої інтегрування А звернемося до першого закону комутації. Так як струм в індуктивності не може змінюватися стрибкоподібно, а до комутації, тобто в момент 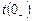він дорівнював нулю, то

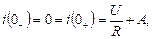
звідки

Тоді закон наростання струму в колі буде

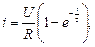
де 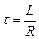має розмірність часу (Гн/Ом=с) і називається сталою часу розглянутого кола.

Перехідний процес часто можна вважати практично закінченим через інтервал часу 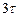з моменту комутації, коли стум досягає значення 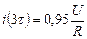. Так як залежність струму від часу знайдена, то можна визначити і залежності від часу напруг на резистивному та індуктивному елементах кола:

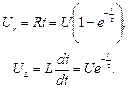
Залежності перехідного процесу 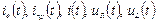представлені на рис. 7.4.

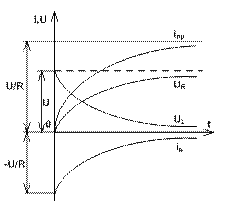
Рис. 7.4. Залежності перехідного процесу при підключенні кола 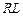до постійної напруги

2. Замикання кола котушки індуктивності зі струмом. Розглянемо перехідний процес в колі котушки індуктивності зі струмом, яке має крім індуктивності 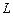активний опір 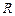, при замиканні її рубильником 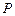(рис. 7.5). Запишемо диференціальне рівняння перехідного процесу в колі після замикання рубильника:

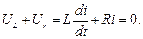
Так як диференціальне рівняння однорідне, то його загальний розв’язок містить тільки вільну складову

,

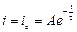де 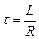– стала часу.

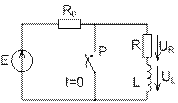
Рис. 7.5. Коротке замикання кола котушки індуктивності

зі струмом

Щоб знайти сталу часу інтегрування А, звернемось до першого закону комутації. До замикання рубильника тобто в момент часу 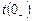в котушці був постійний струм, який дорівнював 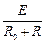, тоді

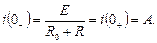
Струм в індуктивності буде дорівнювати

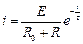
і буде підтримуватися за рахунок енергії, яка накопичилася в її магнітному полі.

Тепер можна визначити залежності напруг на резистивному та індуктивному елементах

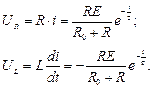
Залежності перехідного процесу 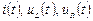зображені
на рис. 7.6.

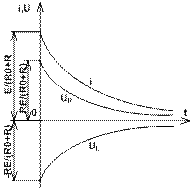
Рис. 7.6. Залежності перехідного процесу при замиканні кола індуктивності зі струмом

3. Підключення джерела постійної напруги до послідовного кола з резистивним і ємнісним елементами. Розглянемо перехідний процес, який виникає в колі заряджання ємнісного елемента від джерела постійної напруги (рис. 7.7).

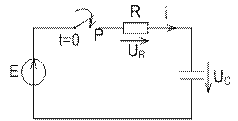
Рис. 7.7. Увімкнення кола 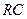до постійної напруги

Складемо диференціальне рівняння для кола після замикання рубильника в момент :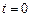

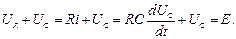
Загальний розв’язок неоднорідного диференціального рівняння подамо як суму двох складових .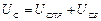

Перша складова відповідає примусовому режиму 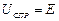, так як зарядка ємнісного елемента закінчиться, коли напруга буде дорівнювати напрузі джерела.

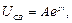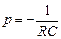Друга складова відповідає вільному процесу. Так як диференціальне рівняння кола першого порядку, то його розв’язок запишеться як де – корінь характеристичного рівняння .

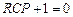Тоді загальний розв’язок запишеться як

Для визначення сталої інтегрування А звернемося до другого закону комутації. Будемо вважати, що до замикання рубильників момент 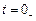, ємнісний елемент не був заряджений. Тому , звідки .

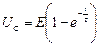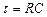Тоді напруга на ємніснім елементі за час заряджання , де стала часу кола, яка визначає швидкість перехідного процесу.

Залежності від часу струму і напруги на резистивному елементі будуть відповідно:

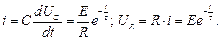
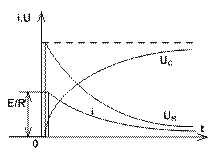
Рис. 7.8. Залежності перехідного процесу при підключенні кола під постійну напругу

4. Розрядка ємнісного елемента через резистивний елемент.

Після замикання ємнісного елемента, зарядженого до напруги 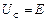, на резистивний елемент з опором 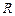(рис. 7.9), в колі виникає струм, обумовлений зміною заряду 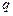ємнісного елемента де знак мінус свідчить про те, що струм – це струм розрядки в контурі, позначений на рис. 7.9 пунктиром, направлений назустріч напрузі на конденсаторі.

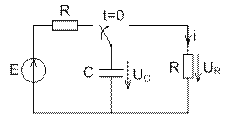
Рис. 7.9. Замикання ємнісного елемента на резистивний елемент

Складемо диференціальне рівняння для контуру який отримали після комутації:

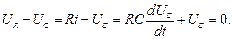
Так як в колі розрядки ємнісного елемента немає джерела ЕРС, то диференціальне рівняння однорідне і його загальний розв’язок має тільки вільну складову:

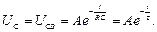
Для визначення сталої А звернемося до другого закону комутації. Так як до комутації тобто в момент 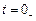ємнісний елемент був заряджений до напруги джерела, то 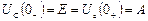. Тоді закон зміни напруги при розрядці ємнісного елемента:

,

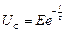де 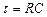– стала часу кола. Розрядний струм буде дорівнювати:

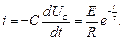
Залежності перехідного процесу при замкненні ємнісного елемента на резистивний елемент приведені на рис. 7.10.

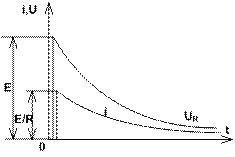
Рис. 7.10. Залежності 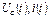при замиканні ємнісного елемента на резистивний елемент

Читайте також:

1. IX. Відомості про військовий облік
2. IX. Відомості про військовий облік
3. V Практично всі психічні процеси роблять свій внесок в специфіку організації свідомості та самосвідомості.
4. Активне управління інвестиційним портфелем - теоретичні основи.
5. Білковий обмін: загальні відомості
6. Біографічні відомості
7. Боротьба з проявами національної самосвідомості
8. Вальниці ковзання. Загальні відомості
9. Види правосвідомості
10. Виникнення і розвиток свідомості у людини.
11. Виникнення людської свідомості. Мова і свідомість.
12. Від них необхідні відомості, документацію і пояснення з питань охоро1

Переглядів: 1010