• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Теоретичні відомості

Коливаннями називаються рухи або процеси, для яких характерна певна повторюваність в часі.

Коливання супроводжуються поперемінними перетвореннями енергії одного виду в енергію іншого виду.

Коливання називаються вільними, якщо вони здійснюються за рахунок спочатку наданої енергії, без подальшої зовнішньої дії на коливальну систему (систему, що здійснює коливання). Коливання називаються вимушеними, якщо вони відбуваються під дією зовнішньої сили, що періодично змінюється.

Гармонійними коливаннями називаються коливання, за яких фізична величина змінюється за законом синуса (або косинуса).

Різні періодичні процеси (процеси, що повторюються через рівні проміжки часу) можуть бути представлені у вигляді суми (суперпозиції) декількох гармонійних коливань.

Гармонійне коливання величини s описується рівнянням

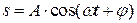, (15.1)

де: А - амплітуда коливання – максимальне значення величини, що коливається; 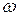– кругова (циклічна) частота; 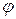– початкова фаза коливання у момент часу ; 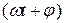– фаза коливання в момент часу t.

Фаза коливання визначає значення коливальної величини в даний момент часу. Оскільки косинус змінюється в межах від +1 до -1, то s може приймати значення від -А до +А. Оскільки 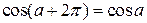, то для гармонійних коливань збільшення (приріст) фази коливання на 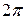призводить до того, що всі величини, які характеризують коливання, приймають початкове значення.

Періодом коливань Т називається якнайменший проміжок часу, після закінчення якого повторюються стани системи (здійснюється одне повне коливання), що коливається і фаза коливання одержує приріст :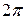

,

Звідки

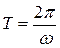. (15.2)

Частотою коливань n називається величина обернена до періоду коливань – кількість повних коливань за одиницю часу:

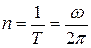. (15.3)

Одиниця частоти – герц (Гц). 1Гц – частота періодичного процесу, для якого за 1 секунду здійснюється одне повне коливання.

Перша (швидкість) і друга (прискорення) похідні за часом від величини s, що гармонійно коливається, також здійснюють гармонійні коливання з тією ж циклічною частотою:

; (15.4)

. (15.5)

З останнього рівняння бачимо, що s задовольняє рівняння

або . (15.6)

Це рівняння називають диференціальним рівнянням гармонійних коливань. Його розв’язок

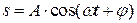. (15.7)

Математичним маятником називається ідеалізована система, що складається з підвішеної на невагомій нерозтяжній нитці довжиною l матеріальної точки масою m, що коливається під дією сили тяжіння без тертя.

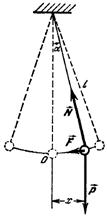Добрим наближенням математичного маятника є невелика важка кулька, підвішена на тонкій довгій нитці.

Для малих кутів відхилення можна вважати: .

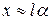Повертаюча (рівнодійна ) сила:

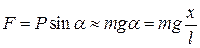. (15.8)

Рівняння руху:

або 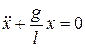. (15.9)

Отже, рух математичного маятника описується диференціальним рівнянням гармонійних коливань, тобто відбувається згідно із законом 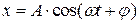з частотою та періодом, відповідно:

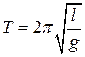, . (15.10)

Фізичним маятником називається тверде тіло, що здійснює під дією сили тяжіння коливання навколо горизонтальної осі підвісу, що не проходить через центр мас тіла.

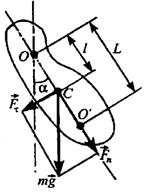Якщо фізичний маятник відхилити від положення рівноваги на деякий кут , то момент повертаючої сили

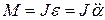. (15.11)

З іншого боку, для малих кутів

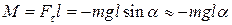, (15.12)

де 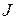– момент інерції маятника відносно осі, що проходить через точку підвісу О, 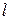– відстань від точки підвісу до центра мас С маятника, 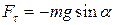– повертаюча сила (із знаком мінус, оскільки вона напрямлена протилежно до напрямку збільшення ).

Відповідн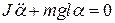о або

. 15.13)

Таким чином, для малих кутів відхилення, фізичний маятник здійснює гармонійні коливання 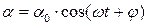з циклічною частотою і періодом:

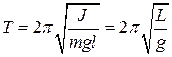, , (15.14)

де довжина 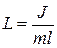– називається приведеною довжиною фізичного маятника.

Приведена довжина фізичного маятника - це довжина такого математичного маятника, який має такий самий період коливань, що і даний фізичний маятник.

Точка на продовженні прямої ОС, що віддалена від осі підвісу на відстань приведеної довжини L, називається центром коливань фізичного маятника.

Математичний маятник можна представити як частковий випадок фізичного маятника, вся маса якого зосереджена в його центрі мас. При цьому , отже .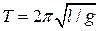

Залежність періоду коливань маятника від прискорення вільного падіння використовують для точних вимірювань прискорення вільного падіння g на поверхні Землі.

Читайте також:

1. IX. Відомості про військовий облік
2. IX. Відомості про військовий облік
3. V Практично всі психічні процеси роблять свій внесок в специфіку організації свідомості та самосвідомості.
4. Активне управління інвестиційним портфелем - теоретичні основи.
5. Білковий обмін: загальні відомості
6. Біографічні відомості
7. Боротьба з проявами національної самосвідомості
8. Вальниці ковзання. Загальні відомості
9. Види правосвідомості
10. Виникнення і розвиток свідомості у людини.
11. Виникнення людської свідомості. Мова і свідомість.
12. Від них необхідні відомості, документацію і пояснення з питань охоро1

Переглядів: 913