• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Рівняння адіабати ідеального газу

У ході будь-якого оборотного процесу газ підкоряється своєму рівнянню стану. Для ідеального газу це рівняння має вид

(21.16)

Бувають процеси, у ході яких газ, крім рівняння стану, підкоряється деякій додатковій умові, що визначає характер процесу. Додаткова умова може полягати, наприклад, у тому, що один з параметрів стану залишається постійним.

Якщо постійний тиск газу, процес називають ізобаричним. У цьому випадку додаткова умова має вид . Якщо залишається незмінним об’єм газу ( ), процес називається ізохоричним. Нарешті, якщо в ході процесу залишається незмінною температура ( 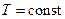), процес називається ізотермічним. З рівняння (21.16) випливає, що у випадку ідеального газу при ізотермічному процесі тиск і об’єм пов'язані співвідношенням

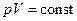, (21.17)

що називається рівнянням ізотерми ідеального газу, а крива, обумовлена цим рівнянням, називається ізотермою.

Процес, що протікає без теплообміну із зовнішнім середовищем, називається адіабатичним. Запишемо рівняння першого закону термодинаміки, і підставимо в нього вираз для енергії (21.7) і роботу у виді :

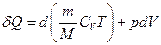. (21.18)

При відсутності теплообміну із зовнішнім середовищем . Тому для адіабатичного процесу рівняння (21.18) спрощується:

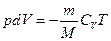(21.19)

Візьмемо диференціал від обох сторін рівняння (21.16), отримаємо

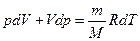. (21.20)

Помножимо рівняння (21.19) на відношення 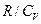і додамо його до (21.20), результатом буде

, (21.21)

де (див. формулу 21.15). Поділимо (21.21) на добуток :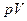

. (21.22)

Ліву частину цього рівняння можна уявити у вигляді , звідки

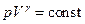(21.23)

Ми отримали рівняння адіабати ідеального газу в змінним 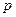і 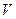. Його називають рівнянням Пуассона.

Запишемо рівняння (21.23) у вигляді 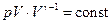і замінимо 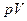у відповідності до (21.16) на 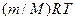, прийдемо до рівняння адіабати ідеального газу в змінних 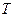і :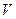

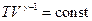(21.24)

(стал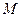і , і 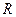ми включили у константу, відповідно, сталі у формулах (21.23) і (21.24) мають різні значення).

З рівняння (21.24) випливає, що при адіабатичному розширенні ідеальний газ охолоджується, а при стиску нагрівається.

Обчислимо похідну для ізотерми та адіабати в одній і тій же точці ( 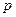, 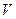). Продиференціюємо рівняння ізотерми (21.17), отримаємо, що , звідки

(для ізотерми).

Диференціювання рівняння адіабати (21.23) дає, що , звідки

(для адіабати).

Таким чином, тангенс кута нахилу дотичної у адіабати в 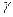разів більше, ніж у ізотерми – адіабата йде крутіше, ніж ізотерма (рисунок 21.1).

Читайте також:

1. V Процес інтеріоризації забезпечують механізми ідентифікації, відчуження та порівняння.
2. VІI. Утворіть вищий та найвищий ступені порівняння від прислівників із вправи VI.
3. Адіабатичний тепловий вибух
4. Асимптотичний підхід до порівняння оцінок
5. Бюджетний контроль - це порівняння показників бюджету зі звітом за від­повідний період часу.
6. В обох випадках основним розрахунковим рівнянням є рівняння теплопередачі і теплового балансу
7. В-21 Дослідження адіабатичного процесу: визначення показника адіабати та кількості ступенів вільності
8. Вивід основного рівняння фільтрації
9. Використання рівняння номінальних витрат за моделлю COCOMO II
10. Внутрішня енергія і теплоємність ідеального газу
11. ВПРАВА 2. Утворіть де можливо, форми ступенів порівняння від поданих прикметників.
12. Гармонічні коливання. Диференціальне рівняння гармонічних коливань та його розв’язок. Амплітуда, фаза, частота, період коливань

Переглядів: 4179