• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Гармонічні коливання. Диференціальне рівняння гармонічних коливань та його розв’язок. Амплітуда, фаза, частота, період коливань

Розділ 5. Коливання і хвилі

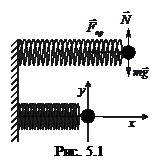Коливаннями називають процеси, які повторюються з певною періодичністю. В залежності від механізму виникнення коливань розглядають механічні, електромагнітні, електромеханічні і т. п. коливання, а в залежності від характеру сил, що діють на коливну систему, – вільні (власні), згасаючі, вимушені тощо.

Розгляд почнемо з власних механічних коливань горизонтального пружинного маятника, який складається з тіла масою m, закріпленого до кінця пружини, що жорстко прикріплена до стінки (рис. 5.1).

Якщо вивести тіло з положення рівноваги, то на нього почне діяти повертаюча сила пружної деформації пружини, яка задається законом Гука 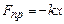. Якщо знехтувати тертям і масою пружини у порівнянні з масою тіла, то при невеликих деформаціях пружини закон руху – ІІ закон Ньютона – запишеться як

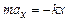, (5.1)

де k – коефіцієнт пружності (жорсткість пружини), х – зміщення тіла від положення рівноваги, а_х – прискорення вздовж осі Х. В подальшому всяку силу, пропорційну до зміщення і напрямлену до положення рівноваги, будемо називати квазіпружною, незалежно від її природи.

Оскільки прискорення 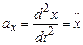, то (5.1) можна переписати як

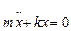
або

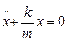. (5.2)

У рівнянні (5.2) 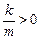, тому можна ввести позначення

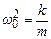, (5.3)

де 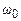називають власною циклічною частотою коливань.

Підставляючи (5.3) у (5.2), одержимо диференціальне рівняння коливань не тільки пружинного маятника, але усякого тіла (матеріальної точки), на яке діє квазіпружна сила:

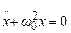. (5.4)

Легко показати, що розв’язком цього рівняння є гармонічні функції (рис. 5.2)

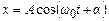або 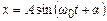. (5.5)

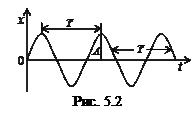Коливання, в яких зміна фізичної величини в залежності від часу відбувається за законом синуса або косинуса, називаються гармонічними. В (5.5): А – амплітуда коливань – найбільше значення коливної фізичної величини (у даному випадку, максимальне зміщення від положення рівноваги), 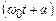– фаза коливань, a – початкова фаза.

Проміжок часу, протягом якого здійснюється одне повне коливання, називається періодом коливань Т. Зрозуміло, що , оскільки гармонічні функції повторюються через 2p. Звідси циклічна частота

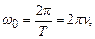(5.6)

де – лінійна частота, як кількість коливань, здійснених за одиницю часу.

Для пружинного маятника 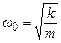, тому період коливань

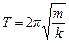. (5.7)

Читайте також:

1. I період – адаптаційний.
2. I. Грецький період (друга половина VII — середина
3. IV-й період Римської держави ( ІІІ – V ст. н. е. ) – пізня Римська імперія
4. L2.T4/1.1. Засоби періодичного транспортування штучних матеріалів.
5. Ni - загальна кількість періодів, протягом яких діє процентна ставка ri.
6. V Процес інтеріоризації забезпечують механізми ідентифікації, відчуження та порівняння.
7. Антропологічна періодизація первісної історії
8. Асимптотичний підхід до порівняння оцінок
9. Багатофазний однопівперіодний випрямляч
10. Байки першого періоду творчості (1850-1870 pp.).
11. Биття та модуляція коливань
12. Біржове страхування (хеджування) учасників біржової торгівлі від несприятливих для них коливань цін

Переглядів: 5247