• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Основні теоретичні відомості

Моментом інерції матеріальної точки відносно даної осі називається скалярна фізична величина, яка дорівнює добутку маси матеріальної точки на квадрат відстані до осі. Для і-тої матеріальної точки тіла

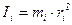. (9.1)

Кожне тіло має деякий момент інерції відносно заданої осі незалежно від того, чи воно обертається, чи покоїться.

Момент інерції тіла відносно даної осі дорівнює сумі моментів інерції матеріальних точок, з яких складається тіло, відносно цієї ж осі

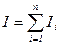. (9.2)

З (9.2) видно, що одиницею вимірювання моменту інерції в СІ є 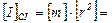1кг·м².

Фізичний зміст моменту інерції полягає в тому, що момент інерції є мірою інертності тіла в обертальному русі, тобто при обертальному русі момент інерції 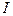відіграє ту саму роль, що маса тіла m при поступальному русі. Але маса є величиною сталою (m=const), а момент інерції тіла залежить від відстані кожної його матеріальної точки до осі обертання ( I=f(r) ).

Моменти інерції тіл залежать від їх мас, розмірів, форми, положення відносно осі. Для однорідних тіл правильної геометричної форми моменти інерції легко визначаються методами інтегрального числення:

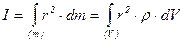, (9.3)

де dm=ρdV – маса елемента об’єму dV тіла; ρ – густина тіла; r – відстань від елементу об’єму dV тіла до осі обертання. Моменти інерції багатьох тіл правильної геометричної форми відносно осі, що проходить через їх центр мас (або інших осей) обчислені та наведені у довідниках і підручниках. Зокрема, для суцільних однорідних диска і циліндра радіуса R і масою m (вони застосовуються в даній роботі) момент інерції відносно осі, що проходить через центр мас перпендикулярно до площини диска визначається формулою

І= 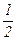mR², (9.4)

Якщо відомий момент інерції тіла відносно осі ОО, що проходить через центр мас тіла (точка С на Рис9.1), то можна знайти момент інерції цього тіла відносно довільної осі z, паралельної осі ОО, за теоремою Штейнера.

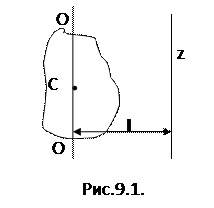Момент інерції тіла відносно довільної осі дорівнює сумі моменту інерції тіла відносно осі, що проходить через його центр мас (центр інерції) паралельно до даної осі, і добутку маси тіла на квадрат відстані l між осями.

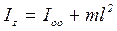. (9.5)

Теорема Штейнера дає можливість визначити момент інерції тіла відносно будь-якої осі через момент інерції відносно осі, що проходить через його центр мас.

Прилади і обладнання: Прилад для дослідної перевірки теореми Штейнера, секундомір, штангенциркуль, лінійка.

Опис установки.Прилад, що використовується в роботі (рис. 9.2) складається із підставки 1, стояка 2, кронштейна 3, диска 6, підвішеного на сталевій дротині 4, і двох циліндрів 5, які можна фіксувати симетрично на диску 6 відносно його центру.

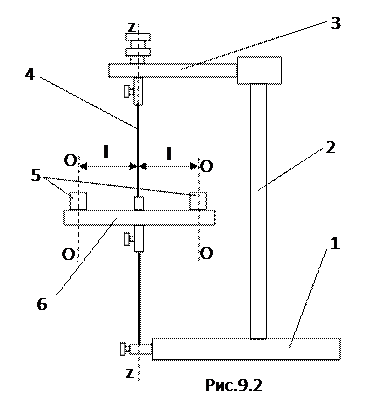Якщо диск без циліндрів змусити здійснювати гармонічні крутильні коливання відносно осі z, що збігається з віссю дротини і проходить через центр мас диска, то період його коливань

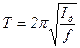, (9.6)

де І_д – момент інерції диска без циліндрів відносно вказаної осі; f – модуль кручення дротини, який чисельно дорівнює моменту сили, що треба прикласти до дротини для закручення її на кут в 1 радіан.

Момент інерції диска відносно його осі симетрії (в нашому випадку вона збігається з віссю z )

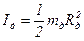, (9.7)

де m_д – маса диска; R_д – радіус диска.

Якщо закріпити на диску два циліндри і змусити цю систему ( диск разом с циліндрами) здійснювати гармонічні крутильні коливання, то період коливань системи ( Т_с ) буде більшим і дорівнюватиме

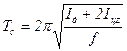, (9.8)

де І_цz – момент інерції одного циліндра відносно осі z, що проходить через центр диска і збігається з віссю дротини;

Розв’язуючи рівняння (9.7) та (9.8) відносно І_цz, знаходимо дослідне значення моменту інерції циліндра.

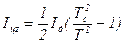. (9.9)

За теоремою Штейнера теоретичне значення моменту інерції одного циліндра відносно осі z

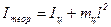, (9.10)

де l – відстань між віссю циліндра і віссю коливань (диска); І_ц - момент інерції одного циліндра відносно осі, що проходить через його центр мас

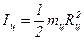, (9.11)

де m_ц – маса циліндра; R_ц – радіус циліндра.

Читайте також:

1. II. Основні закономірності ходу і розгалуження судин великого і малого кіл кровообігу
2. II. Основні засоби
3. II.3. Основні способи і прийоми досягнення адекватності
4. IX. Відомості про військовий облік
5. IX. Відомості про військовий облік
6. V Практично всі психічні процеси роблять свій внесок в специфіку організації свідомості та самосвідомості.
7. VII. ОСНОВНІ ЕТАПИ РОЗВИТКУ УКРАЇНСЬКОЇ КУЛЬТУРИ У ХХ ст.
8. Адвокатура в Україні: основні завдання і функції
9. Активне управління інвестиційним портфелем - теоретичні основи.
10. Амортизація основних засобів, основні методи амортизації
11. Артеріальний пульс, основні параметри
12. Банківська система та її основні функції

Переглядів: 1629