• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Основні поняття

Множини та дії над ними

Поняття множини є одним з найбільш важливих первісних, не означуваних понять математики. Для раціонального аналізу навколишнього світу його уявляють складеним із окремих «об’єктів». Виділення цих об’єктів та зібрань є природнім способом організації математичного мислення.

Під множиною ми розуміємо довільне зібрання визначених же різних об’єктів, що розглядаються як єдине ціле. Об’єкти, з яких складається множина, називаються її елементами. Поняття елемента теж є первісним.

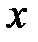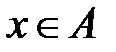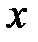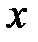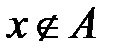Той факт, що об’єкт є елементом множини , позначається символом (читається « належить »). Якщо не є елементом , це позначається (читається « 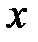не належить »). Множина, що не має елементів, називається порожньою і позначається символом .

Таким чином, множина вважається заданою, якщо про кожний «об’єкт», що розглядається, можна сказати, що він або належить множині , або ні.

Отже, кожна множина характеризується певною ознакою, згідно якої довільний елемент належить чи не належить даній множині.

Приклади множин:

1. Множина всіх символів цієї сторінки.

2. Множина натуральних чисел (позначається ).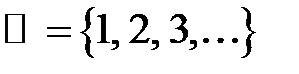

3. Множина цілих чисел (позначається ).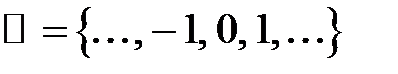

4. Множина дійсних чисел.

Звичайно в конкретних міркуваннях елементи всіх множин, що розглядаються в даній математичній теорії, вибирають із деякої широкої множини (своєї для кожного випадку), яка називається універсальною множиною, або універсумом.

Щоб задати множину, потрібно вказати, які елементи їй належать. Це можна зробити двома способами:

1. Прямим перечисленням елементів множини.

Якщо множина складається з елементів 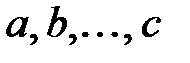, це позначається як .

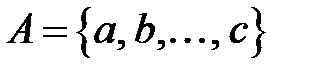2. Характеристичною властивістю (ознакою) елементів множини.

Якщо А — множина всіх елементів 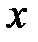універсуму, що мають дану властивість 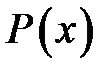, це позначається:

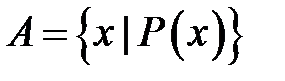, або , чи .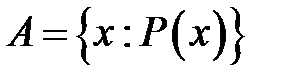

Приклади множин:

1. Множина 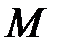парних цілих чисел запишеться как

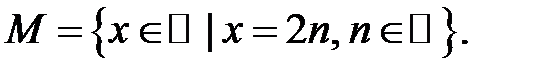
2. Множина раціональних чисел:

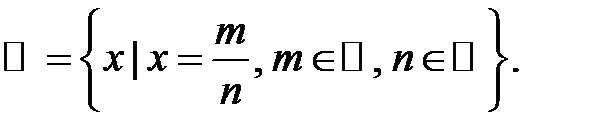
Дві множини 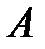і 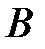називаються рівними, якщо кожний елемент множини 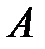є елементом множини 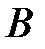і навпаки. Рівність множин 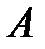і 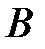позначається як .

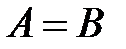З означення рівності випливає, що рівні множини складаються з одних і тих же елементів, причому порядок розміщення елементів множин неістотний, наприклад,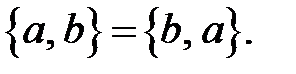

Читайте також:

1. II. Основні закономірності ходу і розгалуження судин великого і малого кіл кровообігу
2. II. Основні засоби
3. II. Поняття соціального процесу.
4. II.3. Основні способи і прийоми досягнення адекватності
5. V. Поняття та ознаки (характеристики) злочинності
6. VII. ОСНОВНІ ЕТАПИ РОЗВИТКУ УКРАЇНСЬКОЇ КУЛЬТУРИ У ХХ ст.
7. А/. Поняття про судовий процес.
8. Адвокатура в Україні: основні завдання і функції
9. Адміністративний проступок: поняття, ознаки, види.
10. Адміністративні правовідносини: поняття, ознаки,
11. Адміністративні провадження: поняття, класифікація, стадії
12. Акти застосування юридичних норм: поняття, ознаки, види.

Переглядів: 567