• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Ініціалізація початкових умов.

У кожній конкретній задачі набір початкових параметрів різний в залежності від того, в якому фазовому просторі розглядається система. Наприклад, в задачі про гармонічний осцилятор необхідно задати імпульс та координату в початковий момент часу (простір ).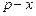

При ініціалізації початкових умов задається точка у фазовому просторі, тобто набір координат та швидкостей для кожної частинки системи. Цей набір визначає енергії системи в цілому (набір координат – потенціальну, набір швидкостей – кінетичну). З одного боку, цей етап досить важливий, оскільки цей набір не повинен виходити за межі фазового простору. З іншого боку, можливо задавати досить умовне співвідношення кінетичної та потенціальної енергії, оскільки через певний час моделювання система сама прийде до певного рівноважного стану, потенціальна та кінетична енергії перерозподіляться. Єдиною умовою є, вибір таких початкових умов, які не дозволять молекулярно-динамічній схемі (чисельному алгоритму) „розійтися”. Крім того, можна змінити і потенціальну. І кінетичну енергії за допомогою процедури перенормування.

Наприклад, для ідеального кристалу, частинки якої в початковий момент часу знаходяться в рівноважних положеннях, розподілимо кінетичну енергію (швидкості) за Максвела відповідно до «стартової» температури , тобто проекції швидкостей мають розподіл

.

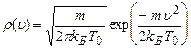Потенціальна енергія системи для частинок у рівноважних положеннях буде мінімальною, а повна енергія системи дорівнюватиме стартовій кінетичній енергії атомів . За досить короткий час (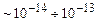с) відбувається релаксація з перерозподілом кінетичної та потенціальної енергії, в результаті чого встановлюється істинна середня температура (при невисоких температурах 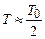). Тому рівноважну температуру в системі можна визначити лише після релаксації.

Читайте також:

1. Виникнення, суть і функції грошей. Особливості функціонування паперових грошей за сучасних умов. Роль золота. «Електронні гроші».
2. Вироблення початкових уявлень про речення і його будову
3. Деградація системи може відбутися за таких умов.
4. Закон вартості: сутність, механізм його дії та функції. Особливості дії закону вартості за сучасних умов.
5. Значення знань з синтаксису в початкових класах
6. Із формули (5.4) випливає, що амплітуда результуючого коливання визначається не тільки амплітудами коливань, що додаються, а й змінюється залежно від різниці їхніх початкових фаз.
7. ІІІ. Дихання за різних умов.
8. Ініціалізація
9. Ініціалізація і встановлення зв'язку
10. Ініціалізація СOM-порту
11. Компоненти готовності майбутнього вчителя початкових класів до застосування інноваційних педагогічних технологій.

Переглядів: 758