
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Перетворення десяткових чисел.
Контрольні завдання
Контрольне завдання містять чотири задачі. Перед розв’язанням кожної задачі вивчіть рекомендуємий матеріал підручника і методичні вказівки до відповідних тем програми. Для закріплення матеріалу додатково проробіть його в робочому зошиті.
При оформленні роботи дотримуйтесь наступних вимог.
1) Обов’язково переписуйте умови задачі з даними для свого варіанту.
2) Відповіді приводьте відразу ж після кожного пункту умови задачі.
3) Умовні графічні позначення цифрових елементів і вузлів приводьте відповідно до ДЕСТ. З цією метою уважно вивчіть Додаток.
4) Сторінки, малюнки, таблиці повинні бути пронумеровані. Малюнки обов’язково підписуйте знизу.
5) Відповіді повинні бути конкретними, короткими, чіткими.
6) Виправлення помилок (роботу над помилками) виконуйте не в тексті контрольної роботи, а після рецензії викладача.
Задача 1
Модуль 1.1Основи обчислювальної техніки
Тема: Системи числення
Завдання 1.1. Згідно з вказаним варіантом переведіть десяткове число А10 у двійкову, двійково-десяткову, вісімкову та шістнадцяткову системи числення. А10=45m,n35, де m-передостання, n-остання цифри залікової книжки, з точністю q-6.
Завдання 1.2. Згідно з заданим варіантом переведіть вісімкове число В8 та шістнадцяткове число С16 у двійкову систему числення, В8 вибирають з таблиці, С16=С m6,nА
| n | ||||||||||
| В8 | 135,35 | 147,74 | 123,56 | 265,33 | 165,67 | 142,53 | 444,33 | 253,61 | 376,12 | 567,55 |
Завдання 1.3. Згідно з заданим варіантом переведіть у десяткову систему числення двійкове число D2, вісімкове число Е8 та шістнадцяткове число F16.
| n | ||||||||||
| D2 | 11101,01 | 10101,11 | 10100,10 | 11010,01 | 10111,01 | 11010,11 | 10011,10 | 11101,01 | 1100,01 | 10111,11 |
| Е8 | 135,35 | 147,74 | 123,56 | 265,33 | 165,67 | 142,53 | 444,33 | 253,61 | 376,12 | 567,55 |
| F16 | А35,35 | B47,74 | C23,56 | D65,33 | E65,67 | F42,53 | A44,33 | B53,61 | C76,12 | D67,55 |
Методичні вказівки по виконанню задачі 1
Вивчіть матеріал відповідно розділу в (6, ст.11-16, 24-25) і методичні вказівки до виконання задачі.
Перетворення десяткових чисел.
Для перетворення десяткового числа у двійкову систему числення число ділять на 2. Остачу у вигляді 0 або 1 записують у молодший розряд двійкового числа. Частку від ділення знов ділять на 2, остачу (0 або 1) записують у наступний після молодшого розряд. Ці дії виконують доти, доки частка від чергового ділення не дорівнюватиме 1. Одиницю записують у старший розряд двійкового числа.
Для перетворення цілого числа X, записаного в системі числення з основою p, на його еквівалент у системі числення з основою q слід ділити X на q до отримання цілої остачі, меншої від q (метод послідовного ділення). Число X у системі числення з основою q подається послідовністю остач ділення в порядку, зворотному їхньому одержанню, причому старшу цифру в числі X дає остання остача.
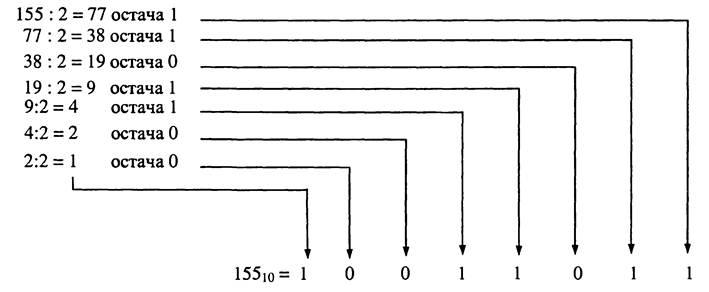
Рис. Перетворення десяткового числа 15510 на двійковий еквівалент
Для чисел, що мають як цілу, так і дробову частину, переведения з од-нієї системи числення в іншу здійснюється окремо для цілої і дробової частин. Для перетворення правильного дробу X, записаного у системі числення з основою р, на його еквівалент в системі числення з основою q слід послідовно множити X на q, причому множити слід тільки дробові частини (метод послідовного множення). Еквівалент X у системі числення з основою q подається у вигляді послідовності цілих частин результате множення у порядку їхнього одержання, причому старший розряд є цілою частиною першого результату. Якщо необхідно виконати перетворення з точністю q , то кількість послідовних множень дорівнює к.
Приклад.Записати десятковий дріб 0,36610 з точністю 2-8 у двійковій системі числення.
Дробові частини заданого числа та чисел, що утворюються у результаті множення, 8 разів послідовно множимо на 2 (рис.).
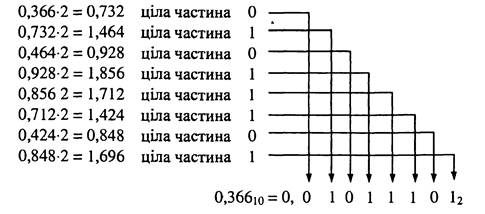
Рис. Перетворення десяткового числа 0,36610 на двійковий еквівалент з точністю 2-8
Двійково-десяткова система числения - система, у якій кожну десяткову цифру від 0 до 9 подають 4-розрядним двійковим еквівалентом.
Приклад.Перетворити десяткове число 369110 на двійково-десятковий код. При перетворенні кожну цифру десяткового числа перетворюють на двійковий 4-розрядний еквівалент:

Отже, 369110 = 0011 0110 1001 00012-10
Для перетворення вісімкового числа на двійковий еквівалент кожну його цифру замінюють двійковою тріадою:
Отже, 65218 = 1101010100012
Для перетворення шістнадцяткового числа на двійковий еквівалент кожну шістнадцяткову цифру слід замінити на двійковий еквівалент - тетраду.
 |
| Шістнадцяткове число | F | |
| Двійкове чило |
Отже, 7F16 = 011111112.
Переведення числа D в десяткову систему числення:
D2=1101,01=1*23+1*22+1*20+1*2-2=8+4+1+0,25=13,2510
Переведення числа Е в десяткову систему числення:
E8=423,16=4*82+2*81+3*80+1*8-1+6*8-2=+56+7+0,25+0,078=275,2187510
Переведення числа F в десяткову систему числення:
F16=F71,3D=15*162+7*161+1*160+3*16-1+13*16-2= =3840+112+1+0,188+0,051=3953,23910
Перетворення двійкового числа на десятковий еквівалент.Під кожним бітом двійкового числа записують десяткові значения кожної позиції. Десяткові числа підсумовують. Приклад перетворення двійкового числа 101101102 на десятковий еквівалент наведено у таблиці.

Перетворення вісімкового числа на десятковий еквівалент. Кожну цифру вісімкового числа множать на відповідну вагу позиції. Сума цих добутків дає десяткове число. Приклад перетворення вісімкового числа 23578 на десятковий еквівалент наведено у таблиці.
 |
Перетворенняшістнадцяткового числа на десятковий еквівалент.
Кожну цифру шістнадцяткового числа множать на відповідну вагу позиції. Сума цих добутків дає десяткове число. Приклад перетворення шістнадцяткового числа 2С6Е16 на десятковий еквівалент наведено у таблиці.

Читайте також:
- Адаптивні хвилькові перетворення : Хвилькові пакети.
- Введення чисел.
- Визначення перетворення за Лапласом
- Визначення режиму вибухового перетворення хмари ГППС
- Визначення. Матриці, отримані в результаті елементарного перетворення, називаються еквівалентними.
- Визначте соціальні перетворення в процесі радянізації українського суспільства.
- Виконаємо лінійне перетворення
- Вимірювальні сигнали, перетворення вимірювальних сигналів, форми вимірювальної інформації
- Вирішення проблеми не міститься в існуючому знанні та не може бути отримане шляхом перетворення наявної наукової інформації.
- Вирішення проблеми не міститься в існуючому знанні та не може бути отримане шляхом перетворення наявної наукової інформації.
- Відношення порядку на множині дійсних чисел.
- Відношення порядку на множині невід’ємних раціональних чисел.
| <== попередня сторінка | | | наступна сторінка ==> |
| | | Задача 2 |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |