
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Тема 3. Задача лінійного програмування та методи її розв’язування
Якщо цільова функція та обмеження оптимізаційної задачі містять змінні в першому або нульовому степені, то вона називається лінійною, або задачею лінійного програмування (ЛП):

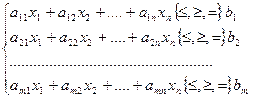 .
.
Задачу лінійного програмування можна представити у канонічній формі, коли обмеження є рівностями, а всі bі ≥0 (і = 1, 2, …, m).
Приклад 3.1
Записати в канонічній формі задачу лінійного програмування
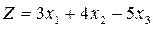 ® max
® max

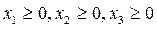 .
.
Розв’язання
Перше обмеження вже має вигляд рівняння, тому його залишаємо. У другого права частина (-90) від’ємна (b2 ≤ 0), відповідно, цю нерівність помножаємо на -1. У результаті всі коефіцієнти і знак нерівності змінюються на протилежні:
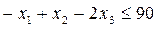 .
.
Тепер потрібно перетворити його на рівняння. Оскільки знак нерівності ≤, додаємо до лівої частини додаткову змінну  :
:
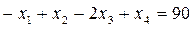 .
.
У третього обмеження знак ≥0, тому від нього додаткову змінну  треба відняти:
треба відняти:
 .
.
Отже, задача ЛП прийме наступний вигляд:
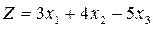 ® max
® max

Будь-яку задачу лінійного програмування можна розв’язати за допомогою надбудови «Поиск решения» в Excel, симплекс-методом, а якщо кількість невідомих дорівнює двом (задача є двовимірною), то ще й графічним методом.
Приклад 3.2
Розв’язати задачу ЛП, використовуючи Excel:

Розв’язання
Підготуємо в Excel наступну форму, заповнивши її нашими даними:

Чарунки В3:E3 залишаємо порожніми, це значення змінних, їх потім підрахує комп’ютер.
У F6 вставляємо формулу =СУММПРОИЗВ(B3:E3;B6:E6). Це значення цільової функції, яка прямує до максимуму.
У F9 вводимо =СУММПРОИЗВ($B$3:$E$3;B9:E9). Натискаємо на нижній правий кут цієї чарунки і тягнемо мишу до себе, не відпускаючи її ліву кнопку, заповнивши клітинку F10.
У меню зверху обираємо «Данные →Поиск решения». Якщо надбудову «Поиск решения» не вдається знайти, її можна встановити, натиснувши «Настройка панели быстрого доступа → Надстройки → Поиск решения → Перейти». Заповнюємо діалогове вікно пошуку рішення:

Коли заповнюємо обмеження, не забуваємо, що масив обов’язково порівнюється з масивом ($B$3:$E$3>=$B$4:$E$4), а чарунка з чарункою ($F$9<=$H$9).
Натискаємо «Выполнить».

Як бачимо, оптимальний план: 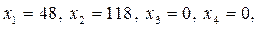 що забезпечує максимальне значення цільової функції Z=1564.
що забезпечує максимальне значення цільової функції Z=1564.
Приклад 3.3
Розв’язати задачу ЛП графічним методом



Розв’язання
Побудуємо графіки кожної прямої і позначимо штрихом півплощини, задані нерівностями.
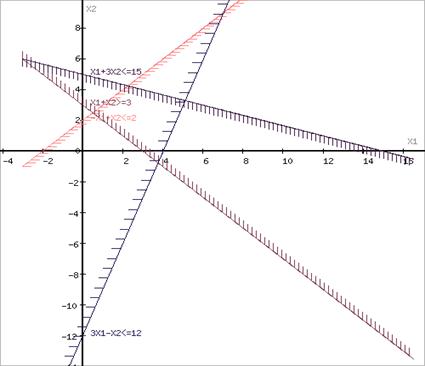
Визначимо область допустимих значень (многокутник ABEDC).
Прирівняємо цільову функцію задачі до  і побудуємо графік цієї прямої. Так як цільова функція прямує до мінімуму, будемо рухати пряму
і побудуємо графік цієї прямої. Так як цільова функція прямує до мінімуму, будемо рухати пряму  паралельно до першого дотику з многокутником ABECD (точка С).
паралельно до першого дотику з многокутником ABECD (точка С).
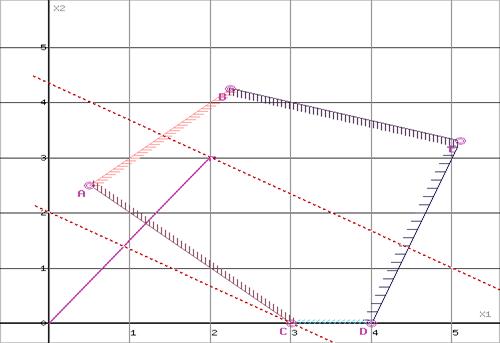
Оскільки точка С отримана в результаті перетину прямих x2=0 та x1+x2≥3, розв’яжемо систему рівнянь

Отримаємо розв’язки x1 = 3, x2 = 0.
Мінімальне значення цільової функції Z=2*3 + 3*0 = 6.
Приклад 3.3
Розв’язати задачу ЛП симплекс-методом
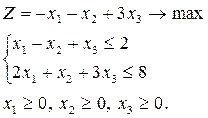
Для побудови першого опорного плану приведемо систему обмежень до канонічного вигляду шляхом введення додаткових змінних.

Перший опорний план задачі:
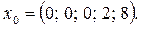
Для цього початкового плану значення цільової функції дорівнює:

Складемо симплексну таблицю для першого опорного плану задачі (табл. 3.1).
Таблиця 3.1
Застосування симплекс-методу – 1 ітерація
| Базис | Сбаз | План | -1 | -1 | θ | |||
| х1 | х2 | х3 | х4 | х5 | ||||
| x4 | -1 | |||||||
| x5 | 22/3 | |||||||
| Zj – Cj ≥ 0 | -3 | - |
Поточний опорний план неоптимальний, оскільки в індексному рядку знаходиться від’ємне значення (-3). У якості розв’язувального обираємо стовпчик, що відповідає змінній x3.
Визначимо симплексні відношення θ,поділивши кожен елемент стовпчику «План» на відповідне значення розв’язувального стовпчика (враховуються тільки додатні значення розв’язувального стовпчика). Серед них обираємо найменше (2). Таким чином, перший рядочок буде розв’язувальним (напрямним).
Розв’язувальний елемент (1) знаходиться на перетині розв’язувальних стовпчика та рядочка.
Змінну x4 виключаємо з базису. Замість неї вводимо x3.
Треба зробити, щоб на місці розв’язувального елемента стояла одиниця, а замість усіх інших значень розв’язувального стовпчика були нулі. Для цього здійснюємо перетворення за методом Жордана-Гаусса. Ділимо всі елементи напрямного рядочка на значення розв’язувального елемента. Записуємо отримані значення в нову симплекс-таблицю. Від усіх інших елементів старої симплекс-таблиці віднімаємо відповідні значення тільки що отриманого рядочку, помножені на елементи розв’язувального стовпчика.
Нова симплекс-таблиця (табл. 3.2) виглядатиме наступним чином:
Таблиця 3.2
Застосування симплекс-методу – 2 ітерація
| Базис | Сбаз | План | -1 | -1 | θ | |||
| х1 | х2 | х3 | х4 | х5 | ||||
| x3 | -1 | - | ||||||
| x5 | -1 | -3 | 1/2 | |||||
| Zj – Cj ≥ 0 | -2 | - |
Поточний опорний план неоптимальний, оскільки в індексному рядку знаходиться від’ємне значення (-2). У якості розв’язувального обираємо стовпчик, що відповідає змінній x2.
Визначимо симплексні відношення θ. Оскільки у першому рядочку міститься від’ємний елемент, рахувати для нього симплексне відношення не будемо. Для другого рядочку, який буде розв’язувальним, симплексне відношення дорівнює 2/4, тобто ½.
Ділимо всі елементи другого рядочка на 4. Від першого старого рядочка віднімаємо другий новий, помножений на -1.
Отримаємо нову симплекс-таблицю (табл. 3.3):
Таблиця 3.3
Застосування симплекс-методу – 3 ітерація
| Базис | Сбаз | План | -1 | -1 | |||
| х1 | х2 | х3 | х4 | х5 | |||
| x3 | 21/2 | 3/4 | 1/4 | 1/4 | |||
| x2 | -1 | 1/2 | -1/4 | -3/4 | 1/4 | ||
| Zj – Cj ≥ 0 | 31/2 | 11/2 | 1/2 |
Оскільки індексний рядочок не містить від’ємних елементів, знайдений оптимальний план: х1=0, х2=1/2, x3=21/2, х4=0, х5=0.
Питання для самостійного вивчення: загальна та векторно-матрична форми задач ЛП, розв’язування задач ЛП симплекс-методом із штучними змінними (М).
Читайте також:
- I. ЗАГАЛЬНІ МЕТОДИЧНІ ВКАЗІВКИ
- II. УЧЕБНЫЕ И МЕТОДИЧЕСКИЕ ПОСОБИЯ, ПРАКТИКУМЫ
- Автоматизація водорозподілу на відкритих зрошувальних системах. Методи керування водорозподілом. Вимірювання рівня води. Вимірювання витрати.
- Агрегативна стійкість, коагуляція суспензій. Методи отримання.
- Адаптовані й специфічні методи дослідження у журналістикознавстві
- Адміністративні (прямі) методи регулювання.
- Адміністративні методи - це сукупність прийомів, впливів, заснованих на використанні об'єктивних організаційних відносин між людьми та загальноорганізаційних принципів управління.
- Адміністративні методи управління
- Адміністративні, економічні й інституційні методи.
- Адміністративно-правові (організаційно-адміністративні) методи мотивації
- Адміністративно-правові методи забезпечення економічного механізму управління охороною довкілля
- Аерометоди
| <== попередня сторінка | | | наступна сторінка ==> |
| Частина книги, періодичного, продовжуваного видання | | | Тема 5. Цілочислове програмування |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |