
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Прямокутна пластинка. Рішення Нав’є
Рішення основного рівняння згинання (5.15) для прямокутної пластинки в замкнутій формі одержати не вдається. Його доводиться шукати у вигляді нескінченного ряду. Розглянемо шарнірно обперту по контуру прямокутну пластинку (рис. 5.9), що перебуває під дією поперечного навантаження інтенсивністю 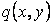 , що змінюється за будь-яким законом. Початок координат розташуємо в куті пластинки. Розмір пластинки в напрямку осі
, що змінюється за будь-яким законом. Початок координат розташуємо в куті пластинки. Розмір пластинки в напрямку осі  дорівнює
дорівнює 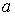 , а в напрямку осі
, а в напрямку осі 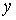 —
—  .
.
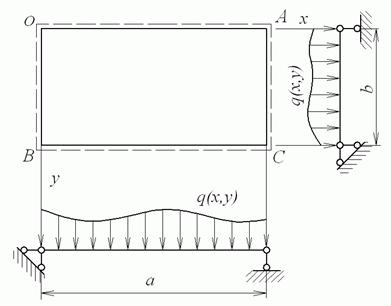
Рис. 5.9. Шарнірно обперта пластинка
Рішення рівняння (5.15) будемо шукати у вигляді подвійного тригонометричного ряду по синусах:
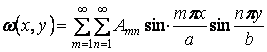 , (а)
, (а)
де 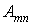 — постійні числа, коефіцієнти ряду;
— постійні числа, коефіцієнти ряду; 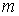 і
і 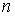 — цілі позитивні числа: 1, 2, 3, …
— цілі позитивні числа: 1, 2, 3, …
Ряд (а) можна представити в розгорнутому виді:
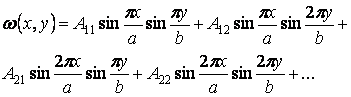
Для шарнірно обпертої по контуру пластинки маємо наступні граничні умови:
при  й
й 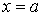
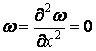 ; (а)
; (а)
при 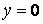 й
й 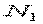
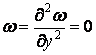 . (б)
. (б)
Переконаємося, що ряд (а) задовольняє цим умовам. Дійсно, на грані пластинки 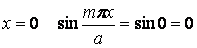 й, отже, прогин
й, отже, прогин 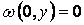 . На грані
. На грані 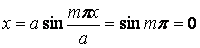 , а значить, і прогин
, а значить, і прогин 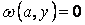 . Точно так само обертаються в нуль прогини на гранях
. Точно так само обертаються в нуль прогини на гранях 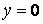 і
і 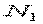 .
.
Отже, граничні умови (б) і (в) відносно прогинів виконуються.
Другі похідні функції прогинів
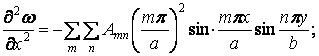
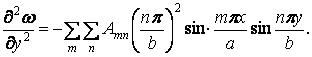
містять синуси тих же аргументів, що і сама функція. Тому похідні звертаються в нуль на всіх гранях пластинки: при 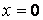 ,
, 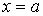 ,
, 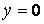 і
і 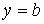 . Отже, граничні умови (б) і (в) для згинальних моментів також виконуються.
. Отже, граничні умови (б) і (в) для згинальних моментів також виконуються.
Визначимо коефіцієнти ряду (а). Для цього підрахуємо четверті похідні функції прогинів
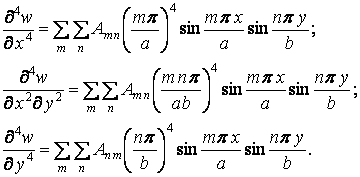
і підставимо їх у рівняння (8.15). Після спрощення одержимо
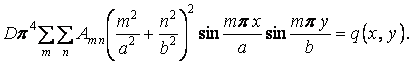
| (г) |
Щоб визначити коефіцієнти ряду, що входить у ліву частину рівняння (г), необхідно і праву частину цього рівняння розкласти в тригонометричний ряд. Представимо навантаження у вигляді подвійного тригонометричного ряду Фур'є по синусах у прямокутній області 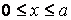 ;
; 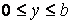 :
:
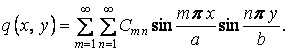
| (д) |
Коефіцієнти цього ряду визначаються по формулі, відомої з курсу математичного аналізу:
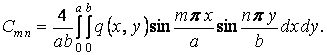
| (е) |
Підставляючи ряд (д) у рівняння (г), одержуємо
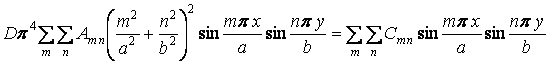 .
.
Два ряди рівні між собою, якщо рівні їх відповідні члени. Таким чином,

Підставляя сюди замість 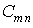 вираз (е), знаходимо коефіцієнти ряда (а) у такій формі:
вираз (е), знаходимо коефіцієнти ряда (а) у такій формі:
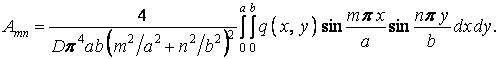
| (ж) |
Отже, функція (а) є рішенням поставленої задачі, тому що вона задовольняє умовам на контурі пластинки і при виборі коефіцієнтів ряду у формі (ж) задовольняє основному рівнянню згинання пластинки. Подальша конкретизація задачі залежить від виду функції 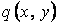 .
.
Розглянемо деякі окремі випадки.
1. Навантаження рівномірно розподілене по всій поверхні пластинки (рис. 5.10). У цьому випадку 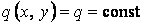 .
.
Рис. 5.10. Вплив розподіленого навантаження
Тоді, відповідно до формули (ж),
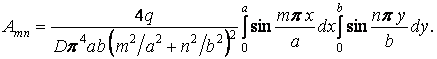
| (з) |
Після інтегрування одержуємо
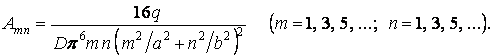
Підставляючи значення цих коефіцієнтів у ряд (а), знаходимо вираз функції прогинів:
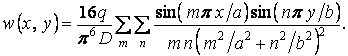
| (5.20) |
Максимальний прогин, що виникає в центрі пластинки (при 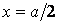 й
й 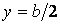 ), становить
), становить
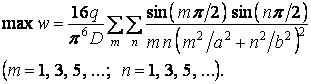
Підставляючи сюди значення циліндричної жорсткості (5.7) і виносячи за дужки 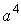 , одержуємо
, одержуємо
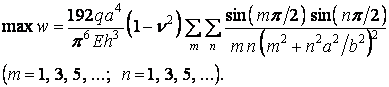
Для практичного використання одержуваних результатів формують таблиці. У цих цілях останню формулу зручно представити в такому вигляді: 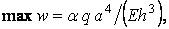
де коефіцієнт
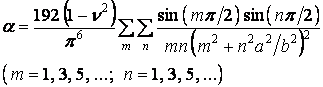
залежить тільки від відношення сторін пластинки 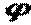 . Ряд, що входить сюди швидко сходиться. Так, зберігаючи перші чотири члени ряду й приймаючи
. Ряд, що входить сюди швидко сходиться. Так, зберігаючи перші чотири члени ряду й приймаючи 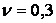 , для квадратної пластинки
, для квадратної пластинки 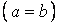 знаходимо
знаходимо
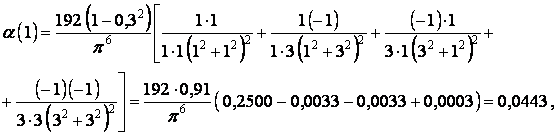
що відповідає точному значенню, що приводиться в довідковій літературі.
Підставляючи функцію прогинів (5.20) у формули (5.8), одержимо згинальні моменти:
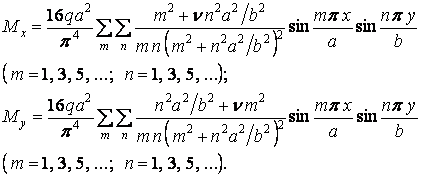
Максимальні згинальні моменти виникають у центрі пластинки (при 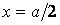 й
й 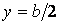 ):
):
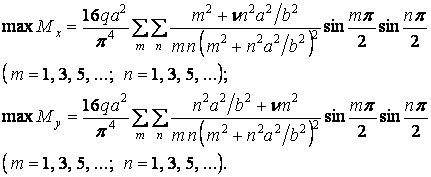
Для складання таблиць їх представляють у вигляді
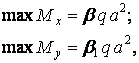
де коефіцієнти 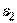 і
і 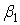 є функціями відношення сторін пластинки
є функціями відношення сторін пластинки 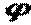 . Ряди в цих функціях сходяться повільніше, ніж у функції
. Ряди в цих функціях сходяться повільніше, ніж у функції 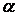 . Так, якщо підрахувати коефіцієнт
. Так, якщо підрахувати коефіцієнт 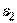 для квадратної пластинки, зберігаючи перші чотири члени ряду, одержимо
для квадратної пластинки, зберігаючи перші чотири члени ряду, одержимо
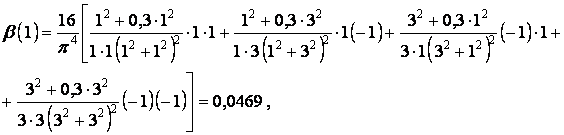
у той час як точне значення, що приводиться в таблицях, 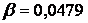 . Отже, при збереженні чотирьох членів ряду значення коефіцієнта
. Отже, при збереженні чотирьох членів ряду значення коефіцієнта 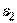 відрізняється від точного його значення на 2,1 %.
відрізняється від точного його значення на 2,1 %.
Значення поперечних сил знайдемо, підставивши функцію прогинів (5.20) у формули (5.9):
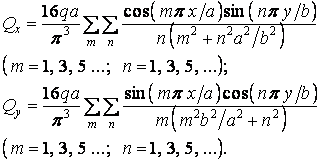
Максимальні значення поперечні сили одержують посередині сторін контуру пластинки. Так, 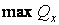 виникає в точках з координатами
виникає в точках з координатами 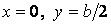 й
й 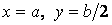 , a
, a 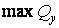 — у точках з координатами
— у точках з координатами 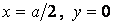 й
й 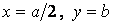 :
:
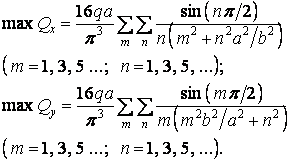
Для табулювання ці функції представляють у такому вигляді:
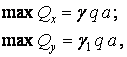
де коефіцієнти 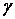 і
і 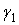 є функціями відношення сторін пластинки
є функціями відношення сторін пластинки 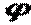 . Ряди в цих функціях сходяться ще повільніше, ніж у функціях
. Ряди в цих функціях сходяться ще повільніше, ніж у функціях 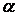 ,
, 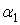 ,
, 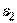 і
і 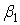 . Так, зберігаючи, як і в попередніх випадках, те ж число членів ряду, для квадратної пластинки одержуємо
. Так, зберігаючи, як і в попередніх випадках, те ж число членів ряду, для квадратної пластинки одержуємо
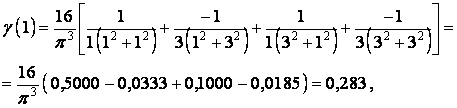
що відрізняється від точного значення, рівного 0,338, на 16,3%.
2. Сила P зосереджена в точці K з координатами 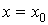 й
й 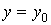 (рис. 5.11).
(рис. 5.11).
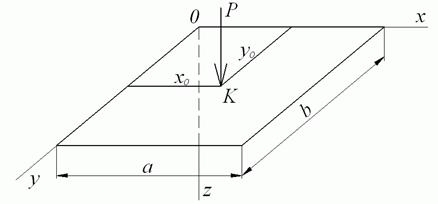
Рис. 5.11. Вплив зосередженої сили
Представимо цю силу у вигляді навантаження, розподіленого на нескінченно малій площі 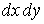 навколо точки K:
навколо точки K:
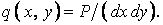
При обчисленні подвійного інтеграла у формулі (ж) варто врахувати, що він звертається в нуль у всіх точках, крім K, де він дорівнює

Підставляючи це значення в зазначену формулу, одержуємо вираз коефіцієнтів ряду (а):
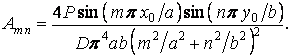
а підставляючи цей вираз в ряд (а), знаходимо функцію прогинів пластинки:
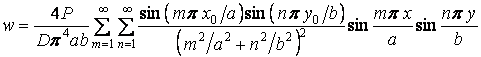
| (5.21) |
Отриманий ряд сходиться повільніше, ніж ряд (5.20).
Знаючи функцію прогинів, звичайним шляхом можна знайти згинальні моменти, поперечні сили й крутні моменти. Ряди, що входять у них, сходяться ще гірше, тому викладена методика може бути рекомендована тільки для знаходження прогинів. Для обчислення ж згинальних моментів, а тим більше, поперечних сил, вона нераціональна.
Читайте також:
- IX. Зміст рішення про результати розгляду скарги та його вручення
- VII розділ. Маркетингові рішення з розподілу та збуту товару
- Алгоритм прийняття рішення при прийманні сигналів з випадковою початковою фазою
- Аналіз отриманих результатів, прийняття рішення про можливість видачі сертифікату відповідності
- Аналогія права - вирішення справи або окремого юридичного питання на основі принципів права, загальних засад і значення законодавства.
- Арешт коштів на рахунку платника податків здійснюється виключно на підставі рішення суду, шляхом звернення органу державної податкової служби до суду.
- Багатокритерійні завдання і можливі шляхи їхнього рішення.
- Вашингтонська конференція та її рішення
- Вибір рішення в умовах невизначеності
- Визнання та виконання міжнародного комерційного арбітражного рішення
- Виконання рішення про виселення боржника та вселення стягувача
- Виконання рішення про відібрання дитини
Переглядів: 813
| <== попередня сторінка | | | наступна сторінка ==> |
| Умови на контурі пластинки | | | Прямокутна пластинка. Розв’язок Леві |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |