Новини освіти і науки:

G+

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Прямокутна пластинка. Розв’язок Леві

Розв’язок Л. Нав’є, розглянутий в попередньому параграфі, придатний тільки для прямокутних пластинок, шарнірно обпертої по контуру. Більш загальним є розв’язок М. Леві. Він придатний для прямокутної пластинки, два протилежних краї якої шарнірно обперті, а два інших мають будь-яке закріплення (защемлення, шарнірне обпирання) або вільні.

У пластинки, зображеної на рис. 5.12, шарнірно обпертими є краї OC і AB.

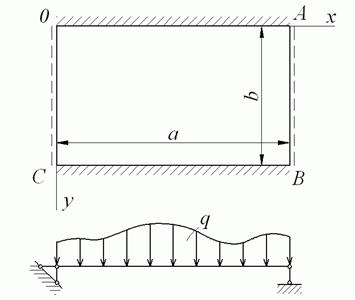
Рис. 5.12. Пластинка із двома шарнірно обпертими краями

Граничні умови на цих краях такі:

пр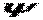и й

(а)

Щоб виконати ці умови, функцію прогинів можна взяти у вигляді

(б)

де Y — довільна функція одного аргументу y; .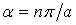

Тому що при й 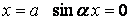, то функція (б) задовольняє умовам (а) відносно прогинів. Щоб перевірити умови (а) для згинальних моментів, підраховуємо другі частинні похідні функції прогинів (б) по x і y:

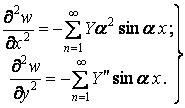
(в)

Пр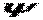и й 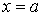ці похідні, аналогічно самій функції, звертаються в нуль і, отже, умови (а) відносно згинаючих моментів також виконуються.

Функція (б) повинна задовольняти основному рівнянню вигину пластинки. Підставляючи її четверті похідні в рівняння (5.15), одержуємо

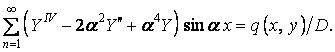
(г)

Для розв’язання рівняння (г) розкладемо його праву частину в тригонометричний ряд Фур'є по синусах:

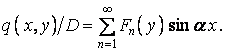
(д)

Коефіцієнти ряду Фур'є 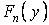є тут функцією y. Тому що розкладання виконується на відрізку 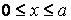, то їх визначають по відомій з курсу математичного аналізу формулі

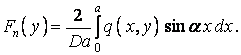
(е)

Підставимо ряд (д) у рівняння (г):

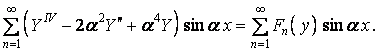
Виносячи знак підсумовування за дужки, одержуємо

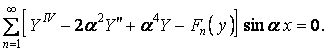
Ця умова виконується, якщо кожний член ряду дорівнює нулю:

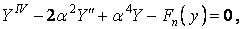
або

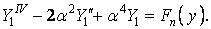
(ж)

Розв’язок однорідного диференціального рівняння четвертого порядку (ж) дорівнює сумі загального розв’язку відповідного однорідного рівняння і якого-небудь частинного розв’язку неоднорідного рівняння. Однорідне рівняння має вигляд

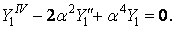
(з)

Його розв’язок можна представити так:

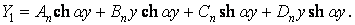
(и)

Позначивши частинний розв’язок рівняння (ж), одержимо його загальний розв’язок:

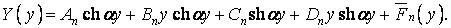
(к)

Підставляючи функцію 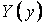у формулу (б), знаходимо

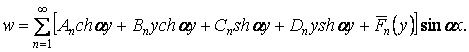
(л)

Функція є розв’язком рівняння (5.15) у випадку поперечного навантаження 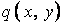, розподіленого на поверхні пластинки за будь-яким законом, і, як показано вище, задовольняє граничним умовам на шарнірно обпертих краях OC і AB.

Розглянемо побудову частинного розв’язку . Відповідно до правила Коші, частинний розв’язок неоднорідного диференціального рівняння четвертого порядку виражається інтегралом

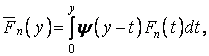
(м)

де 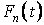— права частина розв'язуваного рівняння, що визначається виразом (е) при заміні аргументу y на t, а 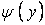— частинний розв’язок відповідного однорідного рівняння. Воно задовольнить умовам

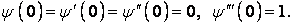
(н)

При розгляді однорідного рівняння (з) відповідно до формули (і) отримані чотири незалежних частинних розв’язки: 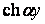, , 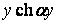, 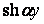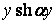. З них умовам (н) задовольняє тільки наступна комбінація:

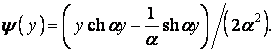
(о)

Замінивши у функціях (о) і (е) аргументи й підставивши ці функції у формулу (м), одержимо шуканий частинний розв’язок рівняння (ж):

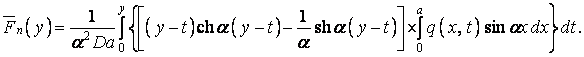
Для визначення довільних сталих 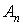, , 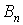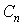і 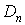використовуємо граничні умови на краях OA і BC. Розглянемо пластинку, у якої ці краї жорстко затиснені (рис. 5.12). Тоді маємо наступні граничні умови:

при 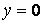й

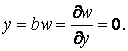
Підставивши в них функцію прогинів (б), одержимо:

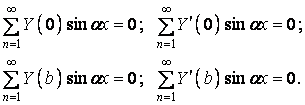
Тому що ці умови повинні виконуватися при будь-яких значеннях аргументу x, то

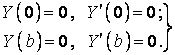
(п)

Вносячи в умови (п) функцію (к), одержуємо систему рівнянь для визначення сталих:

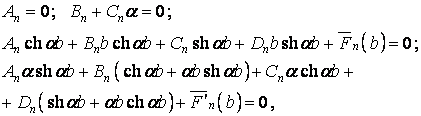
звідки

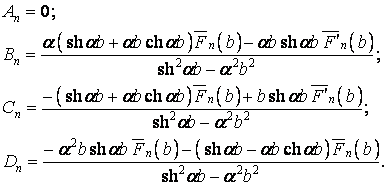
При інших закріпленнях країв OA і BC виходять інші значення сталих.

Ряди у функції прогинів і її похідних сходяться значно швидше, ніж тригонометричні ряди в розв’язку Л. Нав’є, тому розв’язок М. Леві більш зручний в практичних розрахунках навіть прямокутної пластинки, шарнірно обпертої по всьому контурі.

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
Прямокутна пластинка. Рішення Нав’є	\|	Поняття про розрахунок прямокутної пластинки й нескінченної смуги на пружній основі

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.005 сек.