Поняття про розрахунок прямокутної пластинки й нескінченної смуги на пружній основі

Розглянемо прямокутну пластинку, що лежить на суцільній пружній основі й, що перебуває під дією поперечного навантаження інтенсивністю 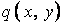(рис. 5.13). Знизу до пластинки прикладені сили реактивного тиску пружної основи (протидія основи), що представляє собою невідому функцію координат .

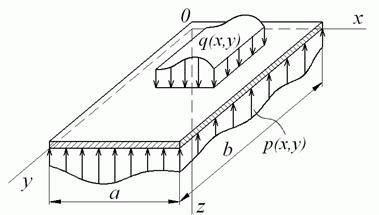
Рис. 5.13. Пластинка на пружній основі

Розрахунок базується на гіпотезах Кірхгофа. Крім того, передбачається, що існує безперервний контакт між пластинкою й підставою, а сили тертя й зчеплення між пластинкою й поверхнею пружної основи відсутні. При таких допущеннях рівняння (5.16) приймає наступний вид:

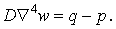
(а)

Значення реактивного тиску на пластинку залежить від переміщення точок підстави. У цей час існує цілий ряд гіпотез про зв'язок між функціям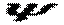и й . Найбільш простою є гіпотеза німецького вченого Э. Вінклера про пропорційність реактивного опору прогинам у відповідних точках:

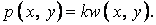
Вона одержала велике поширення завдяки своїй простоті, але має ряд серйозних недоліків і не завжди приводить до правильних результатів.

Підходячи до задачі з позицій теорії пружності, підставу можна розглядати як пружний півпростір, а у випадку плоскої задачі - як пружну напівплощину.

Щоб установити залежність між 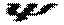і , скористаємося розв’язком задачі про дію тиску 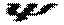на поверхню пружного півпростору. У випадку безперервного розподілу тиску по навантаженій площі F вертикальні переміщення точок поверхні пружного півпростору визначаються наступною залежністю:

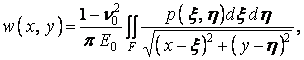
(б)

де 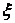й 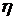— координати центра нескінченно малої навантаженої площі й 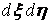(рис. 5.14); x і y — координати точки A, у якій визначається переміщення; 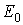і 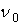— пружні характеристики підстави.

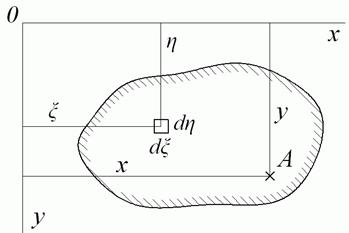
Рис. 5.14. До визначення вертикального переміщення

Розв’язок задачі про відшукання функції прогинів 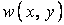зводиться до розв’язання системи двох — інтегрального (а) і диференціального (б) — рівнянь із задоволенням умов на контурі пластинки. Подальший хід розрахунку пов'язаний з обчисленням напруг і деформацій по формулах (5.6) і (5.5).

Прикладом нескінченної смуги на пружній основі може служити стрічковий фундамент. Якщо навантаження уздовж фундаменту постійне, то він перебуває в умовах плоскої деформації. Це означає, що досить розглянути виділену в поперечному напрямку смужку довжиною a і шириною, рівною одиниці (рис. 5.15).

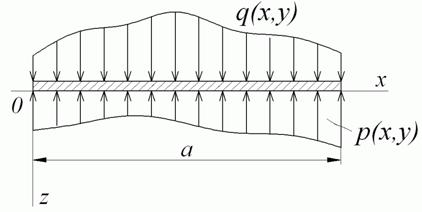
Рис. 5.15. Нескінченна смуга на пружній основі

Для такої смужки диференціальне рівняння прогинів (а) приймає вигляд

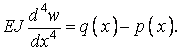
(в)

Залежність (б) між прогинами й реактивним тиском перетвориться до наступної:

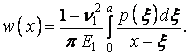
(г)

Сюди входять пружні сталі 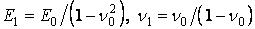, тому що розглядається плоска деформація.

Таким чином, задача про відшукання прогинів нескінченної смуги на пружній основі зведена до розв’язання системи двох інтегро-диференціальних рівнянь (в) і (г).

Розв’язки систем рівнянь (а), (б) і (в), (г) отримані головним чином у працях радянських учених. На підставі цих розв’язків складені докладні таблиці для розрахунку пластинок на пружній основі.

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
Прямокутна пластинка. Розв’язок Леві	\|	Основні рівняння вигину круглої пластинки

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.015 сек.