
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Коливань і його розв’язок
Усі реальні системи є дисипативними. Енергія механічних коливань такої системи поступово витрачається на роботу проти сил опору, тому вільні коливання завжди згасаючі - їх амплітуда поступово зменшується.
Для пружинного маятника масою m, що здійснює малі коливання під дією пружної сили 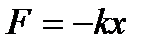 , сила опору пропорційна до швидкості, тобто
, сила опору пропорційна до швидкості, тобто
 ,
,  .
.
де r – коефіцієнт опору.
Другий закон Ньютона для згасаючих коливань має такий вигляд:
 ,
,  .
.
Введемо позначення
 ,
,  .
.
де  – коефіцієнт згасання, а
– коефіцієнт згасання, а  – частота, з якою здійснювались би вільні коливання за відсутності опору середовища. Цю частоту називають власною частотою системи.
– частота, з якою здійснювались би вільні коливання за відсутності опору середовища. Цю частоту називають власною частотою системи.
Тоді другий закон Ньютона можна записати у вигляді
 .
.
Розв’язок цього рівняння має вигляд
 ,
,
де  – амплітуда згасаючих коливань, а AO – початкова амплітуда. Амплітуда згасаючих коливань зменшується з плином часу і тим скоріше, чим більший коефіцієнт опору і чим менша маса т коливного тіла.
– амплітуда згасаючих коливань, а AO – початкова амплітуда. Амплітуда згасаючих коливань зменшується з плином часу і тим скоріше, чим більший коефіцієнт опору і чим менша маса т коливного тіла.
Величина  називається власною циклічною частотою коливань дисипативної системи.
називається власною циклічною частотою коливань дисипативної системи.
Графік залежності х від часу наведено на рис.1

| Рис. 67 |
 .
.
Величину Т тому називають періодом згасаючих коливань.
Якщо A(t) і А(t+T) – амплітуди двох послідовних коливань, що йдуть одне за одним через проміжок часу T, то відношення
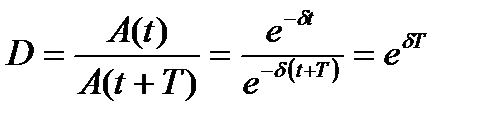 .
.
називаєтьсядекрементом згасання, а його натуральний логарифм
æ=  – логарифмічний декремент загасання.
– логарифмічний декремент загасання.
Позначимо τ проміжок часу, протягом якого амплітуда коливань зменшується в е разів. Тоді
 .
.
Звідси  або
або  .
.
Коефіцієнт загасання δ є фізична величина, обернена до проміжку часу, протягом якого амплітуда зменшується в е разів. Час τ називається часом релаксацій.
Нехай N – кількість коливань, після яких амплітуда коливань зменшується в е разів. Тоді  , æ
, æ  .
.
Логарифмічний декремент згасання æ є фізична величина, обернена до кількості коливань N, після закінчення яких амплітуда зменшується в е разів.
Добротністю коливальної системи називається величина Q, яка дорівнює добутку 2п на відношення енергії Е(t) коливальної системи в довільний момент часу t до зменшення цієї енергії за проміжок часу від t до t+T:
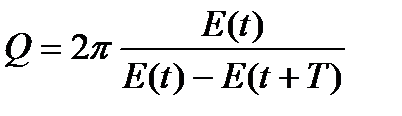 .
.
Лекція №21
48. Диференціальне рівняння вимушених
коливань і його розв’язок. Резонанс
Розглянемо коливання, що їх здійснює система, якщо на неї, крім пружної сили kx і сили опору  , діє ще додаткова періодична сила F, яку називатимемовимушуючою силою i яка змінюється за гармонічним законом
, діє ще додаткова періодична сила F, яку називатимемовимушуючою силою i яка змінюється за гармонічним законом
 .
.
Диференціальне рівняння вимушених коливань, що відбувається вздовж осі ОХ , має такий вигляд:
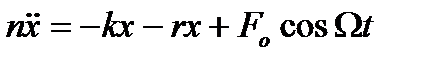 ,
,  ,
,
де  ,
,  ,
,  .
.
Припустимо, що усталені вимушені коливання системи, які виникають під дією сили F, також є гармонічними, тобто
 ,
,
причому їх циклічна частота дорівнює циклічній частоті вимушуючої сили.
Задача полягає в знаходженні амплітуди А і початкової фази φ.
Підставивши вирази для  ,
,  і х удиференційне рівняння вимушених коливань, отримуємо:
і х удиференційне рівняння вимушених коливань, отримуємо:
 ,
,
де введено позначення
 ,
,  ,
,  ,
,  .
.

| Рис. 68 |
 , потім під кутом
, потім під кутом 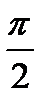 відносно вектора
відносно вектора  проти годинникової стрілки побудуємо вектор
проти годинникової стрілки побудуємо вектор  і вектор
і вектор  , який повернутий на кут
, який повернутий на кут 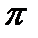 відносно вектора
відносно вектора  . Додавши три вектори
. Додавши три вектори  ,
,  ,
,  , отримаємо вектор
, отримаємо вектор  (рис. 2).
(рис. 2).
З рис. 2 видно, що
 ,
,
і, відповідно,
 .
.
Звідси 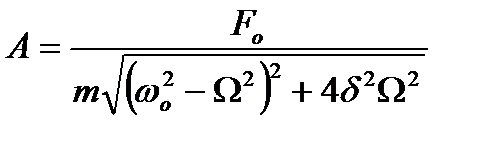 .
.
Амплітуда усталених вимушених коливань прямо пропорційна до амплітуди вимушуючої сили Fo, обернено пропорційна масі т системи i зменшується із збільшенням коефіцієнта згасання.
Із рис. 2 можна отримати значення φ – зсув мас між зміщенням і вимушуючою силою:
 .
.
Розв’язок диференціального рівняння вимушених коливань дорівнює сумі загального розв’язку однорідного рівняння
 ,
,
де  і частинного розв’язку
і частинного розв’язку  неоднорідного рівняння. Доданок x1 відіграє помітну роль лише на початковій стадії процесу виникнення коливань.
неоднорідного рівняння. Доданок x1 відіграє помітну роль лише на початковій стадії процесу виникнення коливань.
Якщо Fo, т і δ сталі, то амплітуда усталених вимушених коливань залежить тільки від співвідношення між циклічними частотами вимушуючої сили (Ω) і вільних коливань системи (ωo).

| Рис. 69 |
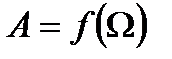 (рис. 3) при різних значеннях коефіцієнта загасання δ. Чим менше δ, тим вище і правіше лежить максимум кривої. Якщо Ω=0, то
(рис. 3) при різних значеннях коефіцієнта загасання δ. Чим менше δ, тим вище і правіше лежить максимум кривої. Якщо Ω=0, то
 .
.
В такому разі коливання не здійснюються, а відхилення Ао називається статичною амплітудою. При  всі криві асиптомічно прямують до нуля. Якщо згасання немає (δ = 0), то амплітуда коливань А зростає із зростанням циклічної частоти
всі криві асиптомічно прямують до нуля. Якщо згасання немає (δ = 0), то амплітуда коливань А зростає із зростанням циклічної частоти  вимушуючої сили і при
вимушуючої сили і при  стає нескінченно великою.
стає нескінченно великою.
Якщо є загасання (  ), то амплітуда досягає максимального значення, коли вираз
), то амплітуда досягає максимального значення, коли вираз 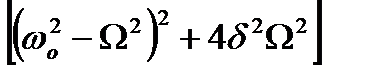 , що є в знаменнику співвідношення для А, досягає мінімуму. Це відбувається, коли
, що є в знаменнику співвідношення для А, досягає мінімуму. Це відбувається, коли
 .
.
Виконуючи диференціювання, отримуємо
 .
.
Це рівняння має два розв’язки:
 ,
,  .
.
Розв’язок  відповідає максимуму знаменника виразу для А. Із інших двох розв’язків лише додатний має фізичний сенс. Отже,
відповідає максимуму знаменника виразу для А. Із інших двох розв’язків лише додатний має фізичний сенс. Отже,
резонансна частота – частота, при якій амплітуда А коливань досягає максимального значення, – має такий вигляд:
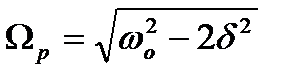 .
.
Явище різкого зростання амплітуди вимушених коливань при наближенні частоти вимушуючої сили до частоти  називається резонансом.
називається резонансом.
Для консервативної системи (  )
)  , а для дисипативної системи
, а для дисипативної системи  трохи менша від власної частоти
трохи менша від власної частоти  системи. Підставивши
системи. Підставивши  у вираз для амплітуди А, отримаємо вираз для амплітуди при резонансі:
у вираз для амплітуди А, отримаємо вираз для амплітуди при резонансі:
 .
.
При малому згасанні ( 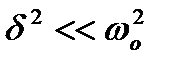 ) амплітуда при резонансі приблизно дорівнює
) амплітуда при резонансі приблизно дорівнює
 .
.
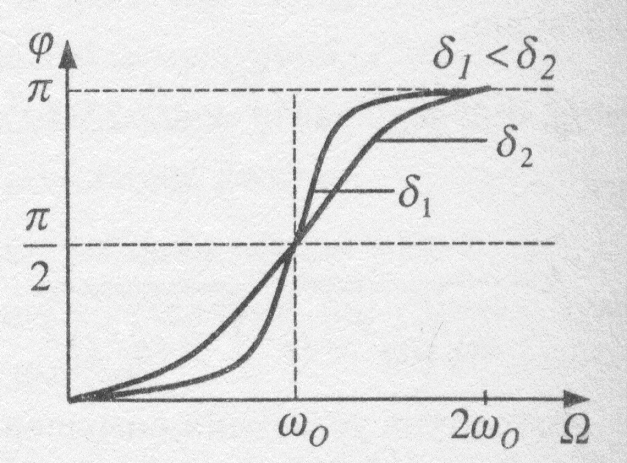
| Рис. 70 |
З виразу  видно, що у випадку
видно, що у випадку  зміщення коливної системи і вимушуюча сила мають однакові фази; у всіх інших випадках
зміщення коливної системи і вимушуюча сила мають однакові фази; у всіх інших випадках  . Залежність
. Залежність  від
від  при різних значеннях
при різних значеннях  наведена на рис. 4.
наведена на рис. 4.
Лекція №22
49. Вимушені коливання у електромагнітному коливальному контурі. Кола змінного струму.
Закон Ома
| U |
| ~ |
| R |
| I |
Розглянемо електричне коло, яке складається із джерела змінного струму та опору R.
Нехай струм у колі змінюється за законом:
 .
.
Тоді напруга на опорі R змінюється за законом:
 .
.
| U |
| ~ |
| L |
 , то напруга на котушці рівна е.р.с. самоіндукції за модулем
, то напруга на котушці рівна е.р.с. самоіндукції за модулем
 ,
,
де  ,
,  , де
, де  – індуктивний опір.
– індуктивний опір.
Векторна діаграма співвідношення струму та спаду напруги має вигляд:
| U0L |

|
| I |
Якщо у коло включений конденсатор, то спад напруги на ньому змінюється за законом:

| U |
| ~ |
| С |
 ;
;  .
.
 .
.
Як слідує із рівняння, зміна напруги на конденсаторі відстає від струму по фазі на кут  . Величина
. Величина  – зветься ємнісним опором.
– зветься ємнісним опором.
Для постійного струму 
 .
.
| U0С |

|
| I |
| U |
| ~ |
| С |
| R |
| Uав |
| а |
| в |
| L |
| j |
| І |
| UoR |
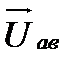
|

|

|
 , то спад напруги Uав необхідно визначати слідуючим чином:
, то спад напруги Uав необхідно визначати слідуючим чином:
 .
.
 .
.
 .
.
Тоді величину 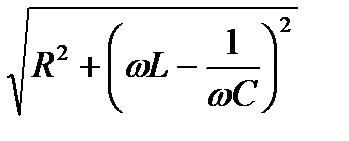 можна трактувати як повний опір кола Z, а зв’язок між струмом, напругою та повним опором виразити рівністю:
можна трактувати як повний опір кола Z, а зв’язок між струмом, напругою та повним опором виразити рівністю:
 ,
,
яка зветься законом Ома для змінного струму.

|
 – зміщення по фазі. При паралельному з’єднанні елементів R, L, C векторна діаграма має вигляд:
– зміщення по фазі. При паралельному з’єднанні елементів R, L, C векторна діаграма має вигляд:
| j |

|

|

|

|
а повний опір визначається за формулою
 .
.
50. Резонанс напруг
Нехай у колі із послідовно з’єднаними R, L, С включене джерело е.р.с., яка змінюється за законом:
 .
.
Тоді у колі буде протікати струм
 ,
,
де  ,
,  , а зміщення за фазою визначається
, а зміщення за фазою визначається
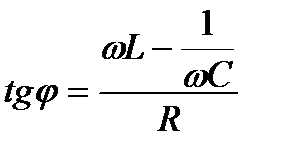 .
.
Проаналізуємо залежність струму Іо від w (частоти е.р.с.).
Якщо  , то
, то  і
і  ,
,  . При збільшенні w реактивний опір
. При збільшенні w реактивний опір  спочатку зменшується, Z – також зменшується, а
спочатку зменшується, Z – також зменшується, а 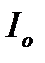 – збільшується.
– збільшується.
| Io |
| w |
| wo |
| R1 |
| R2 |
| R3 |
| R1>R2>R3 |
 реактивний опір зростає, Z – збільшується, а
реактивний опір зростає, Z – збільшується, а  – зменшується (асимптотично).
– зменшується (асимптотично).
| R2>R1 |
| wo |
| R=0 |
| w |
| j |
| R1 |

|

|
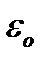 від частоти w має вигляд:
від частоти w має вигляд:
Випадок, коли частота генератора w рівна частоті 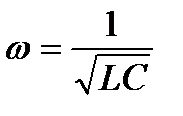 , амплітуда струму досягає максимального значення, а зсув фаз між струмом та напругою дорівнює нулю, зветься резонансом напруг.
, амплітуда струму досягає максимального значення, а зсув фаз між струмом та напругою дорівнює нулю, зветься резонансом напруг.
Розглянемо, чому дорівнюють спади напруг на L та С в момент резонансу.
 .
.
В момент резонансу  .
.
 ,
,
де Q – добротність контура.
Отже 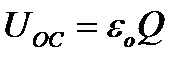 . Аналогічно
. Аналогічно  .
.
При великих добротностях Q, спади напруг UOL та UOC можуть в багато разів перевищувати напругу UOR, а також eо генератора.
51. Розгалуження змінних струмів.
Резонанс струму
| ~ |
| І |
| Іс |
| L |
| R |
| IL |
| U |
| Io=IOR |
| IOC |
| IOL |
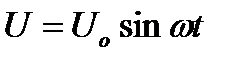 . Тоді
. Тоді  , де
, де  та
та  – визначаються геометрично.
– визначаються геометрично.
При деякому співвідношенні між L та С і w зсув фаз стає рівним нулю, контур поводиться як коло із чисто активним опором, а струм досягає мінімального значення. Цей випадок вимушених коливань зветься резонансом струмів.
52. Робота та потужність змінного струму
Нехай напруга в колі змінюється за законом 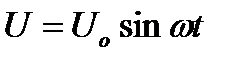 . Якщо у колі Z=R, то
. Якщо у колі Z=R, то  . Миттєва потужність
. Миттєва потужність  . Середнє значення потужності за великий проміжок часу рівне середньому значенню за період.
. Середнє значення потужності за великий проміжок часу рівне середньому значенню за період.
Робота  .
.
За період Т:  ,
,  .
.
 ;
;
Якщо коло містить L, С, то  .
.
Оскільки прилади фіксують ефективне значення струму та напруги, а не амплітудне (Іо, Uо), то
 ,
,  ,
,
тоді  .
.
Лекція №23
53. Утворення хвиль в пружному середовищі.
Поздовжні і поперечні хвилі.
Рівняння біжучої хвилі
Розглянемопружне середовище, між частинками якого існують сили взаємодії, що перешкоджають тому або іншому виду його деформації. Тіло, яке коливається в пружному середовищі, періодично діє на прилеглі до нього частинки середовища, виводячи їх з положення рівноваги і змушуючи здійснювати вимушені коливання. При цьому середовище поблизу тіла деформується і в ньому виникають пружні сили. Ці сили діють як на прилеглі до тіла частинки, намагаючись повернути їх у положення рівноваги, так і на віддаленіші від тіла частинки, виводячи їх з положення рівноваги. Віддаленіші від тіла області середовища поступово втягуються в коливальний рух.
Прогрес поширення коливань в суцільному середовшці, яке неперервно розподілене в просторі і має пружні властивості, називається механічним хвильовим процесом, або механічною хвилею.
При поширенні хвилі частинки середовища не рухаються разом з хвилею, а коливаються біля свого положення рівноваги.Основна властивість всіх хвиль є переннесення енергії без перенесення речовини.
Пружними (або механічними) хвилями називаються механічні збурення, що поширюються у пружному середовищі. Пружні хвилі бувають поперечні і поздовжні.

| Рис. 5 |

| Рис. 6 |
Пружна хвиля називається гармонічною, якщо відповідні їй коливання частинок середовища є гармонічними.
Нехай поперечна гармонічна хвиля поширюється вздовж осі ОХ .

| Рис. 7 |
 частинок середовища, що беруть участь у хвильовому процесі, і відстанню х цих частинок від джерела коливань О для якого-небудь фіксованого моменту часу.
частинок середовища, що беруть участь у хвильовому процесі, і відстанню х цих частинок від джерела коливань О для якого-небудь фіксованого моменту часу.
Відстань між найближчими частинками, що коливаються в однаковій фазі, називаєтьсядовжиною хвилі 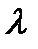 . Довжина хвилі дорівнює тій відстані, на яку поширюється певна фаза коливань за період:
. Довжина хвилі дорівнює тій відстані, на яку поширюється певна фаза коливань за період:
 і
і  .
.
Нехай точка, від якої йдуть коливання, коливається в суцільному середовищі. Коливання поширюються від центра у всі боки.
Поверхня, до якої доходить коливання в деякий момент часу, називається фронтом хвилі.
Фронт хвилі - це поверхня, яка відокремлює частину простору, уже залучену у хвильовий процес, від області, в якій коливання ще не виникли.
Поверхня, в якій всі частинки коливаються в однаковій фазі, називається хвильовою.
Хвильову поверхню можна провести через довільну точку простору, який охоплений хвильовим процесом. Отже, хвильових поверхонь існує нескінченна множина, а хвильовий фронт в кожний момент часу лише один. Хвильові поверхні залишаються нерухомими, а хвильовий фронт весь час переміщується.
Хвильові поверхні можуть бути довільної форми.
Хвиля називаєтьсяплоскою, якщо її хвильові поверхні мають вигляд площин, які паралельні площині, що проходить через джерело хвиль.
Хвиля називаєтьсясферичною, якщо її хвильові поверхні мають вигляд концентричних сфер. Центр цих сфер називається центром хвилі.
Напрямки, в яких поширюються коливання, називаютьсяпроменями. В ізотропному середовищі промені перпендикулярні до фронту хвилі.
Поширення в пружному середовищі механічних збурень, збуджених джерелом хвиль, пов’язане з перенесенням хвилями енергій. Тому такі хвилі називаютьсябіжучими хвилями.
Рівнянням хвилі називається вираз, який дає зміщення коливної частинки як функцію її координат x, y, z і часу t.
Розглянемо плоску хвилю, яка поширюється вздовж осі ОХ і збуджується в площині х = 0 (рис.8). Нехай коливання в цій площині мають вигляд:
 .
.

| Рис. 8 |
 , де
, де  – швидкість поширення хвилі.
– швидкість поширення хвилі.
Отже, коливання частинок, що лежать у площині х, будуть запізнюватись на час  від коливань частинок у площині x=0, тобто матимуть вигляд:
від коливань частинок у площині x=0, тобто матимуть вигляд:

 .
.
Введемо величину, яка називається хвильовим числом:
 .
.
Тодірівняння біжучої плоскої хвилі, що поширюється вздовж осі ОХ , має такий вигляд:
 ,
,
де A – амплітуда коливань, яка називається амплітудою хвилі;  – циклічна частота хвилі;
– циклічна частота хвилі;  – початкова фаза коливань в площині x=0. Величина
– початкова фаза коливань в площині x=0. Величина 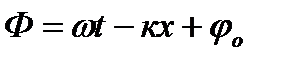 дорівнює фазі коливань у довільній площині з координатою х і називається фазою плоскої хвилі. Зафіксуємо певне значення фази:
дорівнює фазі коливань у довільній площині з координатою х і називається фазою плоскої хвилі. Зафіксуємо певне значення фази:
 .
.
Цей вираз визначає зв’язок між часом t і тим місцем х, в якому фаза має зафіксоване значення. Величина  дає швидкість, з якою переміщається дане значення фази. Продиференціюємо вираз для фааи:
дає швидкість, з якою переміщається дане значення фази. Продиференціюємо вираз для фааи:
 .
.
Звідси
 .
.
Отже, швидкість  поширення хвилі є ніщо інше, як швидкість переміщення фази хвилі і її називають фазовою швидкістю.
поширення хвилі є ніщо інше, як швидкість переміщення фази хвилі і її називають фазовою швидкістю.
Якщо плоска хвиля поширюється в довільному напрямку, то
 ,
,
де  – вектор, який дорівнює за модулем хвильовому числу і має напрям нормалі до хвильової поверхні.
– вектор, який дорівнює за модулем хвильовому числу і має напрям нормалі до хвильової поверхні.
Лекція №24
54. Інтерференція хвиль. Рівняння стоячої хвилі
Якщо в середовищі є декілька джерел коливань, то хвилі, які поширюються від них, йдуть незалежно одна від одної і після взаємного перетину розходяться далі так, ніби такої зустрічі і не було. Це положення називається принципом суперпозиції.
В місцях зустрічі хвиль коливання середовища, які викликані кожною з хвиль, складаються одне з одним. Результат додавання (результуюча хвиля) залежить від співвідношення фаз, періодів і амплітуд хвиль, що накладаються.
Узгоджене проходження в часі і просторі декількох коливань або хвильових процесів пов’язується з поняттям когерентності.

| Рис. 71 |
Інтерференцією хвиль називається явище, яке відбувається при накладанні двох або кількох когерентних хвиль, при якому відбувається стійке в часі їх взаємне підсилення в одних точках простору і ослаблення в інших, залежно від співвідношення між фазами цих хвиль.
Розглянемо накладання двох когерентних косинусоїдальних хвиль, які збуджуються точковими джерелами S1 і S2 (рис.10):
 ,
,  .
.
Амплітуда А результуючої хвилі в точці М дорівнює
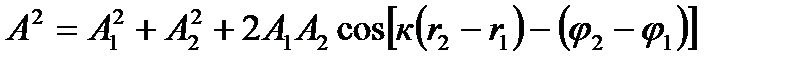 .
.
Оскільки для когерентних джерел різниця початкових фаз  ,то результат інтерференції двох хвиль в різних точках залежить від величини
,то результат інтерференції двох хвиль в різних точках залежить від величини  , яка називається геометричною різницею ходу хвиль.
, яка називається геометричною різницею ходу хвиль.
У точках, де  ,
, 
спостерігається інтерференційний максимум: амплітуда результуючого коливання  .
.
В точках, де  ,
,  спостерігається інтерференційний мінімум: амплітуда результуючого коливання
спостерігається інтерференційний мінімум: амплітуда результуючого коливання
 .
.
m – порядок інтерференційного максимуму або мінімуму.
Оскільки хвильове число  , де
, де 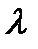 –довжина хвилі в даному середовищі, то при різниці ходу хвиль
–довжина хвилі в даному середовищі, то при різниці ходу хвиль

амплітуда результуючого коливання максимальна. Якщо  , то ця умова набирає вигляду
, то ця умова набирає вигляду
 .
.
Амплітуда результуючого коливання мінімальна в усіх точках, для яких
 .
.
Якщо  , то ця умова набирає вигляду
, то ця умова набирає вигляду
 .
.
При інтерференції хвиль їхня енергія механічно не підсумовується. Інтерференція хвиль призводить до перерозподілу енергії коливань між сусідніми областями середовища.
Особливим випадком інтерференції є стоячі хвилі.
Стоячі хвилі – це хвилі, які утворюються при накладанні двох біжучих хвиль, що поширюються назустріч одна одній з однаковими частотами і амплітудами.

| Рис. 72 |
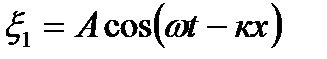 ,
,  .
.
де  – різниця фаз хвиль у точці х=0 (рис.11).
– різниця фаз хвиль у точці х=0 (рис.11).
Додавши ці рівняння і враховуючи, що  , отримаємо рівняння стоячі хвилі:
, отримаємо рівняння стоячі хвилі:
 .
.
Множник 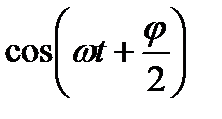 показує, щов точках середовища виникає коливання з тією самою ж частотою
показує, щов точках середовища виникає коливання з тією самою ж частотою  , що і коливання зустрічних хвиль.
, що і коливання зустрічних хвиль.
Множник  , який не залежить від часу, виражає амплітуду Аст, результуючих хвиль, точніше – амплітуда як величина позитивна дорівнює абсолютному значенню цього множника:
, який не залежить від часу, виражає амплітуду Аст, результуючих хвиль, точніше – амплітуда як величина позитивна дорівнює абсолютному значенню цього множника:
 .
.
Амплітуда результуючого коливання залежить від координати х, що визначає положення точок середовища.
У точках середовища, де
 ,
,  ,
,
амплітуда Аст досягає максимального значення 2А. Точки, в яких Аст максимальна,
називаютьсяпучностями стоячої хвилі.
У точках середовища, де
 ,
, 
Аст=0. Ці точки називаютьсявузлами стоячої хвилі. Точки середовища, що знаходяться у вузлах, не коливаються.
Виберемо початок відліку х так, щоб  дорівнювало нулю. Тоді координати пучностей
дорівнювало нулю. Тоді координати пучностей
 ,
,
а вузлів
 .
.
Відстань між двома сусідніми пучностями отримаємо, якщо знайдемо різницю двох значень хn для двох послідовних значень т:
 ,
,
тобто відстань між сусідніми пучностями дорівнює половині довжини тих хвиль, в результаті інтерференції яких утворюється дана стояча хвиля.
Відстані вузла від найближчої пучності дорівнює:
 .
.
Отже, в стоячій хвилі є ряд нерухомих вузлових точок, які розміщені на відстані півхвилі одна від одної. Частинки між вузлами коливаються з різними амплітудами, від нуля у вузлі до подвійної амплітуди у пучності. Всі частинки одночасно проходять через положення рівноваги і одночасно досягають максимальних відхилень, отже, коливаються в однакових фазах. В суміжному інтервалі між вузлами характер коливань такий самий, але фаза протилежна.
У стоячій хвилі енергія не переноситься – повна енергія коливань кожного елемента об’єму середовища обмеженого сусіднім вузлом і пучністю, не залежить від часу. Вона лише переходить з кінетичної енергії в потенціальну енергію пружно деформованого середовища і навпаки. Відсутність перенесення енергії стоячою хвилею є результатом того, що падаюча і відбита хвилі, які утворюють цю стоячу хвилю, переносять енергію в рівних кількості і в протилежних напрямках.
Читайте також:
- Биття та модуляція коливань
- Біржове страхування (хеджування) учасників біржової торгівлі від несприятливих для них коливань цін
- Визначення власних частот коливань системи.
- Визначення форм коливань.
- Використання крутильних коливань для визначення моменту інерції
- Вимірювання сезонних коливань
- Вимірювання сезонних коливань.
- Гармонічні коливання. Диференціальне рівняння гармонічних коливань та його розв’язок. Амплітуда, фаза, частота, період коливань
- Генератори релаксаційних коливань
- ГЛАВА 7. ГЕНЕРАТОРИ ЕЛЕКТРИЧНИХ КОЛИВАНЬ
- Динамічне гасіння коливань.
- Довжиною хвилі є відстань, на яку поширюється хвильовий процес за час одного періоду коливань.
| <== попередня сторінка | | | наступна сторінка ==> |
| Тоді сила струму змінюється у контурі за законом | | | Звукові хвилі та їх властивості. Ефект Допплера. |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |