• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Визначення форм коливань.

При деформації системи її власна частота не дорівнює нулю|нуль-індикатору| . Тоді і . Якщо прийняти, то і епюра кутових координат по довжині пружного зв'язку матиме наступний|слідуючий| вигляд|вид|:

Рис. 21.4

При русі системи без деформації власна частота коливань дорівнює нулю|нуль-індикатору| . Тоді, і . Епюра кутових координат для руху без деформації показана на рис.21.5.

Рис. 21.5

Приклад|зразок| для системи без пружних зв'язків.

Якщо в розглянутій моделі прийняти с1 і с2 прагнуть до нескінченності, то прагне до і прагне до . Розрахункова схема цієї динамічної моделі приведена на Рис. 21.6, де:

Рис. 21.6

IпрS - приведений сумарний момент інерції 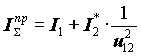; MпрS - приведений сумарний момент зовнішніх сил ; DТ - зміна кінетичній енергії . Рівняння руху для цієї моделі:

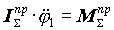
Моделювання динамічних процесів в приводі з|із| пружними зв'язками.

Розглянуті вище рівняння руху механічної системи можна використовувати при моделюванні поведінки цієї системи при різних значеннях її параметрів. Нижче (на Рис. 21.7) приведені результати дослідження впливу жорсткості з на нерівномірність обертання Dw, момент в приводі Мп і на динамічну помилку у.

Рис. 21.7

Контрольні питання до лекції 21.

1. Які завдання|задачі| вирішуються|розв'язуються| в розділі курсу ТММ - динаміка механізмів з|із| пружними ланками ? (стр.1)

2. Який процес в механічних системах називають коливанням, перерахуєте види механічних коливань ? (стр.1-2)

3. Які параметри механічної системи є|з'являються| критеріями адекватності динамічної моделі ? (стр.2)

4. Які допущення приймають при формуванні динамічної моделі ? (стр.2)

5. Як параметри системи приводяться|призводять| до параметрів динамічної моделі ? (стр.3-4)

6. На які складові можна розкласти|розкладати| закон руху динамічної моделі при вимушених|змушених| коливаннях ? (стр.5)

7. Як визначаються власні частоти коливань системи ? (стр.5-6)

8. Які форми коливань існують в двухмассной| механічній системі ? (стр.6)

9. Які параметри системи досліджуються при моделюванні динамічних процесів ? (стр.7)

Читайте також:

1. CMM. Визначення моделі зрілості.
2. I визначення впливу окремих факторів
3. II. Визначення мети запровадження конкретної ВЕЗ з ураху­ванням її виду.
4. II. Мотивація навчальної діяльності. Визначення теми і мети уроку
5. Ocнoвнi визначення здоров'я
6. S Визначення оптимального темпу роботи з урахуванням динаміки наростання втоми.
7. А. Визначення розмірів і площі зони хімічного зараження.
8. Алгебраїчний спосіб визначення точки беззбитковості
9. Алгоритм визначення проекцій точок на поверхнях обертання
10. Алгоритм побудови калібрувального графіка для визначення загального білка сироватки крові
11. Алгоритм побудови калібрувального графіка для визначення загального білка сироватки крові
12. Аналіз існуючих виробів та визначення завдань проекту

Переглядів: 599