• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Використання крутильних коливань для визначення моменту інерції

Визначення моменту інерції неоднорідних тіл і тіл неправильної форми за допомогою інтегрування є складною задачею. У таких випадках моменти інерції визначають експериментально, зокрема, використовуючи метод крутильних коливань.

Суть методу крутильних коливань полягає в такому:

Якщо взяти будь-яке тіло, що закріплене на сталевому стрижні (дротині), і повернути його на деякий кут 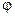відносно осі стрижня, в ньому, внаслідок пружинної деформації кручення, виникне внутрішній момент сил

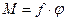, (6.9)

який протидіє закручуючому моменту і протилежний йому за напрямком. Тут 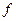- модуль кручення стрижня. Якщо тіло відпустити, то під дією цього внутрішнього моменту сил тіло почне здійснювати крутильні коливання для яких є справедливим закон динаміки обертального руху

,

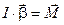де 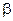– кутове прискорення, .

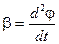В нашому випадку диференціальне рівняння крутильних коливань матиме вигляд:

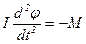або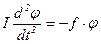

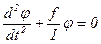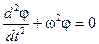, . (6.10)

Розв’язком рівняння (6.10) є функція

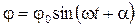, (6.11)

де 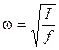- циклічна частота крутильних коливань.

Період крутильних коливань

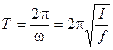. (6.12)

Із формули (6.12) видно, що, при відомому модулі кручення стрижня 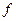та виміряному експериментально періоді коливань 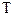, можна обчислити момент інерції тіла.

Для вимірювання момента інерції тіл використаємо крутильний маятник FРМ-05 з відомим значенням модуля кручення 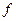. Маятник складається з механічної частини (закріпленої на дротинах рамки), яка може здійснювати коливання, електромагніту, фотоелектричного датчика, універсального мілісекундоміра, який вимірює кількість коливань 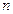і час коливань .

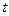Конструкція рамки дозволяє закріплювати в ній досліджувані тіла. Період коливань рамки з тілом, враховуючи (6.12)

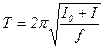, (6.13)

де 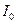– момент інерції рамки; 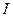– момент інерції досліджуваного тіла, яке досліджується.

Момент інерції 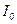рамки маятника невідомий, тому не можна безпосередньо скористатись формулою (6.13) для обчислення моменту інерції 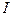досліджу- вального тіла.

Задача розв’язується, якщо спочатку визначити період коливань самої рамки маятника

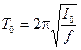, (6.14)

а потім визначити період коливань рамки із зафіксованим в ній тілом:

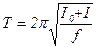(6.15)

Із рівнянь (6.14) і (6.15) знаходим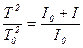о або 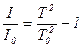, звідси одержимо формулу для обчислення моменту інерції тіл:

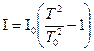(6.16)

Читайте також:

1. CMM. Визначення моделі зрілості.
2. I визначення впливу окремих факторів
3. II. Визначення мети запровадження конкретної ВЕЗ з ураху­ванням її виду.
4. II. Мотивація навчальної діяльності. Визначення теми і мети уроку
5. Ocнoвнi визначення здоров'я
6. S Визначення оптимального темпу роботи з урахуванням динаміки наростання втоми.
7. XIII. Використання амортизаційних відрахувань
8. А. Розрахунки з використанням дистанційного банкінгу.
9. Автогенератори гармонічних коливань на аперіодичних
10. Алгебраїчний спосіб визначення точки беззбитковості
11. Алгоритм побудови калібрувального графіка для визначення загального білка сироватки крові
12. Алгоритм побудови калібрувального графіка для визначення загального білка сироватки крові

Переглядів: 1865