• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Умови на контурі пластинки

Залежно від характеру закріплення країв на контурі пластинки можуть бути задані прогини й кути повороту серединної площини, згинаючі і крутні моменти, поперечні сили. Умови, при яких на контурі задаються переміщення, тобто прогини або кути; повороту серединної площини, називаються геометричними. Умови, при яких на контурі задаються зусилля, тобто згинаючі або крутні моменти й поперечні сили, називаються статичними. Якщо ж задані одночасно і переміщення, і зусилля, то умови називаються змішаними. На кожному краї варто задати дві граничних умови.

Сформулюємо граничні умови для різних випадків закріплення країв прямокутної пластинки (рис. 5.6).

Затиснений край . У защемленні відсутні прогини й неможливий поворот крайового перерізу щодо осі 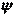. У зв'язку із цим маємо наступні умови:

при

Рис. 5.6. До задавання граничних умов

Шарнірно обперті краї й 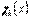. На них дорівнюють нулю прогини і згинальні моменти, тобто й . Виражаючи згинальний момент через прогини пластинки відповідно до формул; (5.8), останню умову можна представити так:

.

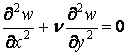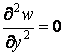Однак при і другій похідній . тому граничні умови на шарнірно обпертих краях і приймають вид

при й

Вільний край . Тут повинні звертатися в нуль згинальний момент , поперечна сила і крутний момент , тобто замість необхідних двох умов з'являються три. Таке протиріччя пов'язане з тим, що задача вирішується приблизно і тому всім граничним умовам точно задовольнити не можна. Однак протиріччя можна усунути, об'єднавши дві останніх умови.

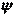Покажемо, що крутний момент і поперечну силу на контурі пластинки можна замінити однією силою, статично їм еквівалентною. Розглянемо крутний момент , розподілений уздовж грані , паралельної ocи (рис. 5.7, а). На довжині діє крутний момент, рівний . Його можна представити у вигляді двох вертикальних протилежно спрямованих сил з плечем (рис. 5.7, б). На нескінченно малому видаленні крутний момент одержить збільшення й буде дорівнює 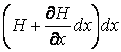. Його також можна представити у вигляді двох вертикальних протилежно спрямованих сил з тим же плечем .

а
б
в

Рис. 5.7. Зусилля на контурі пластинки

Подібну заміну крутних моментів вертикальними силами можна здійснити по всій довжині грані . На границі кожної нескінченно малої ділянки , за винятком крайніх точок і , буде прикладено по дві протилежно спрямовані сили, різниця між якими дорівнює . Отже, уздовж грані буде діяти вертикальна розподілена по її довжині навантаження інтенсивністю (рис. 5.7, в). У точках же й виникнуть зосереджені сили й 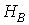. Отримане вертикальне навантаження можна об'єднати з поперечною силою і вважати, що на грані діє наведена поперечна сила інтенсивністю

.

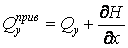(5.17)

Аналогічно, уздовж граней контуру пластинки, паралельних осі 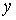, буде діяти приведена поперечна сила інтенсивністю

.

(5.18)

Похідні крутного моменту по 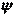й 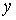знайдемо диференціюванням функції (5.10):

(а)

Підставляючи значення поперечних сил (5.9) і похідних крутного моменту (а) у формули (5.18) і (5.17), одержуємо

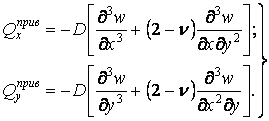
(5.19)

Таким чином, на кожній грані пластинки замість трьох зусиль: згинального моменту, крутного моменту й поперечної сили, - можна розглядати тільки два: згинальні моменти й приведена поперечна сила (позитивні напрямки наведених поперечних сил на всіх гранях, а також зосереджених сил, що виникають у кутах пластинки, показані на рис. 5.8).

Рис. 5.8. Позитивні напрямки зусиль

Отже, на вільній від закріплення грані замість трьох згаданих умов можна вимагати задовільнення лише двох:

.

(б)

Звичайно, при цьому граничні умови будуть задовольнятися приблизно. Але на підставі принципу Сен-Венана заміна поперечної сили й крутного моменту статично їм еквівалентною приведеною поперечною силою викличе лише місцеві напруження поблизу розглянутого краю пластинки

Внесемо в умови (б) вирази згинального моменту (5.8) і приведеної поперечної сили 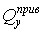(5.19). Тоді на вільній грані , тобто при ,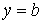

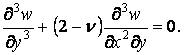
Читайте також:

1. Або зі зберігання інформації та забезпечення доступу до неї, за умови, що ця особа не могла знати про незаконність розповсюдження інформації.
2. Аналітичні умови рівноваги довільної просторової системи сил
3. Аналітичні умови рівноваги системи збіжних сил
4. Аналітичні умови рівноваги часткових випадків систем сил
5. Аналогічно доводиться достатність умови існування максимуму.
6. Аналогія як умовивід
7. Безпосередні умовиводи
8. Блок 4. Умови та охорона праці.
9. Блок перевірки умови
10. БУДОВА ТА УМОВИ ФОРМУВАННЯ ШАРУВАТИХ ТОВЩ
11. Векторні умови рівноваги довільної системи сил
12. Види аудиторських висновків та умови їх надання

Переглядів: 688