• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Диференційне рівняння зігнутої серединної поверхні пластинки

У попередніх параграфах напруження й зусилля в пластинці виражені через прогини її серединної площини. Отже, для визначення напружень і зусиль необхідно знати функцію прогинів .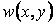

Виріжемо із серединної площини пластинки нескінченно малий елемент розмірами 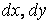і покажемо прикладені до нього зусилля (рис. 5.5).

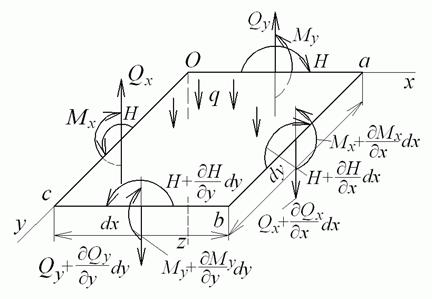
Рис. 5.5. Зусилля в нескінченно малому елементі

На грані діє поперечна сила . На грані , що відстоїть від грані на нескінченно малій відстані 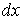, поперечна сила одержує нескінченно мале збільшення і дорівнює .

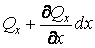Аналогічно, на гранях і діють відповідно поперечні сил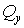и й 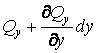. Нормально до серединної площини діє поверхневе навантаження інтенсивністю .

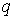Для того щоб розглянутий елемент серединної площини перебував у рівновазі, повинні задовольнятися шість умов рівноваги: три рівняння проекцій сил на координатні осі і три рівняння моментів щодо цих осей. При цьому всі зусилля варто множити на довжину грані, по якій вони діють.

Спроектуємо всі сили, зображені на рис. 5.5, на вісь :

.

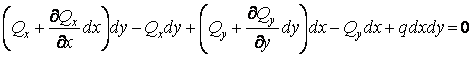Після спрощення одержуємо

.

(5.12)

Рівняння моментів всіх сил щодо осі 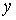має вигляд

Після спрощення одержуємо

.

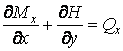(5.13)

Аналогічно, з рівняння моментів щодо осі виходить

.

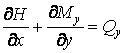(5.14)

Виключимо з рівнянь (5.12)-(5.14) поперечні сили. У результаті одержимо

.

Підставимо в це рівняння вирази моментів (5.8) і (5.10):

,

звідки після спрощення

,

(5.15)

або

.

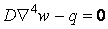(5.16)

Одержали основне рівняння згинання пластинки, яке звичайно називається рівнянням Софі Жермєн. При його інтегруванні з'являться довільні постійні, які повинні бути визначені з умов на контурі пластинки, що залежать від характеру закріплення її країв.

Читайте також:

1. V Процес інтеріоризації забезпечують механізми ідентифікації, відчуження та порівняння.
2. VІI. Утворіть вищий та найвищий ступені порівняння від прислівників із вправи VI.
3. Алгоритм розрахунку температури поверхні чипу ІМС процесора
4. Асимптотичний підхід до порівняння оцінок
5. Бюджетний контроль - це порівняння показників бюджету зі звітом за від­повідний період часу.
6. В обох випадках основним розрахунковим рівнянням є рівняння теплопередачі і теплового балансу
7. В'язкості і тиску повітря від профілю тіла, стану його поверхні і положення тіла в повітряному потоці.
8. Векторне канонічне параметричне рівняння прямої в просторі.
9. Великої питомої поверхні пилинок (відношення площі поверхні до їх
10. Вивід основного рівняння фільтрації
11. Вигляд гортані у розрізі для демонстрації серединної перснеподібної зв’язки
12. ВИЗНАЧЕННЯ МІНІМАЛЬНОГО ЗНАЧЕННЯ ТЕМПЕРАТУРИ НА ВНУТРІШНІЙ ПОВЕРХНІ

Переглядів: 747