• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Рефлексивні, симетричні і транзитивні відношення

Означення 1.3.4. Бінарне відношення R називають рефлексивним у множині 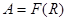, якщо будь-який елемент 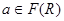перебуває у відношенні сам з собою ( ).

Означення 1.3.5. Бінарне відношення R називають рефлексивним, якщо з того, що слідує, що і .

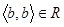Наприклад, відношення 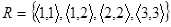рефлексивне у множині 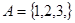, проте не рефлексивне у множині .

Рефлексивними є відношення рівності, подільності, паралельності, конгруентності, подібності фігур, універсальне та діагональне відношення.

Означення 1.3.6. Бінарне відношення R називають антирефлексивним (іррефлексивним) у множині 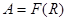, якщо жоден елемент 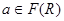не перебуває у відношенні сам з собою ( ).

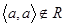Наприклад, відношення 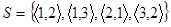антирефлексивне у множині 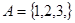. Анти рефлексивними є відношення “не дорівнює”, “менше”, “більше”, перпендикулярності тощо.

Порожнє відношення прийнято вважати як рефлексивним, так і антирефлексивним.

Якщо відношення є ні рефлексивним, ні анти рефлексивним, то його називають не рефлексивним.

Наприклад, відношення не рефлексивне, оскільки елемент 2, на відміну від всіх інших, не перебуває у відношенні сам з собою .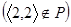

При зображенні рефлексивного відношення з допомогою графіка видно, що всі точки діагоналі належать графіку відношення.

Означення 1.3.7. Бінарне відношення R називають симетричним, якщо з того, що слідує, що .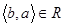

Наприклад, відношення симетричне. Симетричними є відношення паралельності, перпендикулярності, подібності, конгруентності, універсальне відношення тощо.

Для симетричного відношення його графік симетричний відносно діагоналі – бісектриси координатного кута.

Означення 1.3.8. Бінарне відношення R називають антисиметричним, якщо з того, що слідує, що .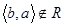

Наприклад, відношення 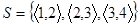антисиметричне. Антисиметричними є відношення включення, “менше”, “більше”, “менше дорівнює” тощо.

Відношення рівності, діагональне та порожнє вважають як симетричними, так і антисиметричними.

Означення 1.3.9. Бінарне відношення R називають транзитивним, якщо з того, що 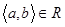і 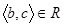слідує, що .

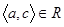Наприклад, відношення 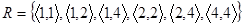транзитивне. Транзитивними також є відношення “менше”, “більше дорівнює”, подільності, паралельності, подібності, включення, діагональне, порожнє та універсальне відношення тощо.

Не транзитивними є відношення “не дорівнює”, перпендикулярності, належності тощо.

Графік транзитивного відношення має властивість 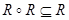і навпаки.

Операція обернення зберігає 5 властивостей відношень: рефлективність, антирефлексивність, симетричність, антисиметричність і транзитивність.

Означення 1.3.10. Відношення R* називають транзитивним замиканням відношення R на множині А, якщо 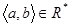тоді і тільки тоді, коли у множині А існує послідовність елементів 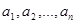така, що 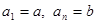і , , ..., .

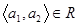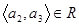Наприклад, нехай 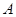– множина точок на площині і , , 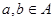якщо точки 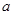і з’єднані відрізком. Тоді 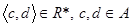, якщо існує ламана лінія, яка з’єднує точки 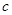і .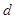

Читайте також:

1. Аналіз співвідношення активів із джерелами їх фінансування
2. Антисиметричність.
3. Антонімічні відношення
4. Багатовимірність людського буття: співвідношення біологічного і соціального в людині
5. Безрозмірною характеристикою гідротрансформатора називається залежність коефіцієнтів пропорційності моментів насосного і турбінного коліс від його передаточного відношення.
6. Бінарне відношення порядку.
7. Бінарні відношення
8. Будь яка передача характеризується передаваємою потужністю та передаточним відношенням.
9. Варіанти співвідношення потреб і виробництва
10. Великої питомої поверхні пилинок (відношення площі поверхні до їх
11. Взаємовідношення біологічного, соціального і духовного в людині.
12. Взаємовідношення віри і розуму, філософії та теології у Фоми Аквінського та пізній схоластиці.

Переглядів: 5788