
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Поняття алгебраїчної операції
Ще в середній школі розглядають різноманітні числові множини: N, Z, Q, R, C. Якщо поставити завдання – проаналізувати, які спільні властивості мають ці множини і чим відрізняються, то прийдемо до висновку, що для цього числові множини слід розглядати не самі по собі, а відносно певних математичних дій або математичних операцій.
N  Z
Z 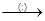 Q
Q 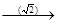 R
R 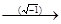 C.
C.
Отже, зазначені множини чисел відрізняються одна від одної здійсненністю або нездійсненністю в них тих чи інших математичних операцій.
У цьому ж проявляється і спільність властивостей цих числових множин. Справді, є операції, які здійсненні у кожній з них. Це дві основні дії арифметики – додавання і множення, відносно яких інші арифметичні дії виступають як залежні, а саме – як обернені. Яку б названих множин ми не взяли, дії додавання і множення можна виконувати над довільними двома елементами цієї множини.
Крім того, основні закони цих дій – комутативний, асоціативний, дистрибутивний – справедливі в кожній з цих множин.
З цього випливає, що однією з найважливіших характеристик числових множин є можливість виконувати над її елементами ті чи інші операції (насамперед, + і *), не виходячи за межі цієї множини.
Наведемо властивості дій додавання і множення.
Властивості додавання:
1) для довільних елементів а і b даної множини існує єдиний елемент с цієї ж множини такий, що 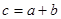 (с називають сумою, а а і b – доданками);
(с називають сумою, а а і b – доданками);
2) асоціативність додавання:  ;
;
3) для довільного елемента а даної множини існує єдиний нульовий елемент q такий, що 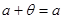 (роль q відіграє 0);
(роль q відіграє 0);
4) для довільного елемента а даної множини існує єдиний протилежний елемент -а такий, що 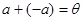 .
.
Властивості множення:
5) для довільних елементів а і b даної множини існує єдиний елемент с цієї ж множини такий, що 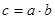 (с називають добутком, а а і b – множниками);
(с називають добутком, а а і b – множниками);
6) асоціативність множення: 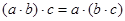 ;
;
7) для довільного елемента а даної множини існує єдиний одиничний елемент е такий, що 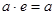 (роль е відіграє 1);
(роль е відіграє 1);
8) для довільного елемента а даної множини існує єдиний обернений елемент а-1 такий, що 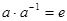 .
.
Властивості додавання і множення аналогічні, тому їх можна об’єднати, якщо назвати елементи q і е нейтральними, а –а і а-1 – симетричними. Очевидно, нейтральний елемент симетричний сам собі.
Означення 3.1.1. Нехай М – множина елементів довільної природи. Кажуть, що в М введено якусь алгебраїчну операцію, якщо довільним двом елементам з даної множини 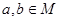 поставлено у відповідність єдиний третій елемент
поставлено у відповідність єдиний третій елемент 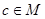 .
.
Довільну бінарну операцію позначають *:
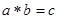 .
.
Отже, операція * є допустимою і однозначною.
Читайте також:
- II. Поняття соціального процесу.
- V. Поняття та ознаки (характеристики) злочинності
- VII. Поняття про рану, рановий процес, види загоювання ран
- А/. Поняття про судовий процес.
- Адміністративна відповідальність: поняття, мета, функції, принципи та ознаки.
- Адміністративний проступок: поняття, ознаки, види.
- Адміністративні провадження: поняття, класифікація, стадії
- Акти застосування юридичних норм: поняття, ознаки, види.
- Активні операції банків
- Активні операції банків з цінними паперами
- Активні операції комерційних банків
- Активні операції центральних банків.
| <== попередня сторінка | | | наступна сторінка ==> |
| Визначення хроматичного числа. Хроматичний поліном | | | Означення і приклади груп |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |