
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Тема 1. Системи числення. Правила переведення цілих та дробових чисел з однієї СЧ в іншу СЧ
1.1 Загальна характеристика систем числення
1.2 Двійкова система числення
1.3 Переведення чисел з однієї позиційної системи в іншу
1.4 Різновиди двійкових систем
1.1 Загальна характеристика систем числення
Система числення – це сукупність позначення прийомів і правил запису числа цифровими знаками. Найбільш відома десяткова система числення, де для представлення чисел використовують цифри від 0 до 9. Числа виникли в глибокій давнині як засіб підрахунку предметів оточуючого середовища. Існує безкінечна кількість способів запису чисел, проте при застосуванні на практиці системи числення повинні мати наступні властивості:
- можливість представлення будь-якого числа в даному форматі;
- однозначність представлення чисел;
- простота виконання операцій над числами.
Системи числення діляться на непозиційні та позиційні, головна відмінність між якими являється в способі визначення значення символу (цифри) в числі.
В непозиційних системах числення значення символу не залежить від його положення в числі. Нехай 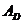 - запис числа системі числення D,
- запис числа системі числення D, 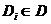 - символи системи, вони складають базу
- символи системи, вони складають базу 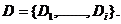 Тоді число
Тоді число 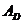 може бути представлене у вигляді:
може бути представлене у вигляді:
 (1.1)
(1.1)
Як слідує з рівняння (1.1), для запису числа використали К символів. 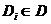 . Очевидно, що в таких системах кількісний еквівалент будь-якої цифри постійний і залежить тільки від її графічного образу.
. Очевидно, що в таких системах кількісний еквівалент будь-якої цифри постійний і залежить тільки від її графічного образу.
Вираз (1.1) характерний для системи числення, яка виникла в Древньому Єгипті в ХХХ столітті до н.е. Кожен символ зображується нерогліфом (від грецького «священна різьба»). Тому ці системи були названі нерогріфічними. Найбільш відомою системою числення являється римська, в якій є знаки I, V, X, L, C, D, M. Вони відповідають числам 1, 5, 10, 50, 100, 500, 1000 відповідно.
В римській системі перші числа натурального ряду від 1 до 10 записуються наступним чином I, II, III, IV, V, VI, VII, VIII, IX, X.
На відміну від (1.1) в римській системі використана, як принцип складання, так і розкладання. Так символ І, поставлений зліва от старшого знака (V, X), зменшує його значення на одиницю. В той же час, символ І, поставлений справа від старшого розряду (V, X), збільшує його значення на одиницю. Цей же принцип діє для будь-якої пари знаків. Так, число 1954 представляється МСMLIV, де CM=900, а IV=4.
Другим представником класу непозиційних систем являється алфавітна система. Найбільш відома грецька система, виникла близько 500 р. до н.е. в Міллеті. Тут для представлення чисел використовувались всі букви алфавіту і деякі старі, вийшовши з вжитку букви.
Непозиційні системи числення мають ряд недоліків:
- відсутність нуля
- безкінечне число символів
- виняткова складність арифметичних операцій.
В позиційних системах числення значення кожної цифри визначається як її виглядом, так і місцем (позицією) в числі. Алфавіт позиційних систем мають обмежене (кінцеве) число символів, що являють цифри. Найбільш відомою є десяткова система , що має алфавіт(базу) {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} і основні 10. Наприклад, число 222 включає 3 однакових цифри, та їм відповідають різні значення. Самому лівому символу відповідає число  наступному – число
наступному – число 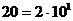 і, на кінець, самому правому – число
і, на кінець, самому правому – число  Цю залежність можна виразити формулою:
Цю залежність можна виразити формулою:
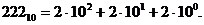 (1.2)
(1.2)
Символ 10 (1.2) означає, що число записано в десятковій системі числення.
В загальному випадку число в позиційній системі записується у вигляді:
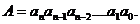 (1.3)
(1.3)
При цьому окрема позиція у виглядів числа називається розрядом, а номер позиції – номером розряду. В загальному випадку число 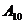 можна задати загальним випадком:
можна задати загальним випадком:
 (1.4)
(1.4)
Цей поліном можна представити скорочено в вигляді:
 (1.5)
(1.5)
Існують системи числення, основна яких відмінна від 10. Як правило, люди використовували для підрахунку пальці. В цьому зв’язку історично існувала 5 система числення (одна рука), десяткова (пальці двох рук), 12 система, 20 система числення (пальці двох рук і ніг). Першою відомою позиційною системою була 60-річна, виникла в древньому Вавилоні близько 2500 років до н.е. Десятинна система була створена в Індії близько VII століття, при цьому нуль появився тільки в IX столітті. Індійські цифри були позичені арабськими купцями, о від них цифри потрапили у Європу.
Нехай для представлення будь-якого розряду числа використовуються цифри 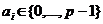 , де р- основні системи числення. Тоді число, записане у вигляді (1.3), відповідає виразу:
, де р- основні системи числення. Тоді число, записане у вигляді (1.3), відповідає виразу:
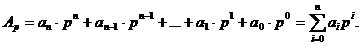 (1.6)
(1.6)
Видно, що р=10 з виразу (1.5) і (1.6) адекватні. Представлені (1.6) відповідають однорідній системі числення, у якій засновані однаково для всіх розрядів. В загальному випадку кожному розряду  може відповідати своя основа
може відповідати своя основа 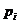 . Це характерне для неоднорідних систем числення, де кількість допустимих символів може бути різноманітне для різних розрядів.
. Це характерне для неоднорідних систем числення, де кількість допустимих символів може бути різноманітне для різних розрядів.
Прикладом неоднорідної системи числення являється система підрахунку часу, для якої молодший розряд  (секунди), другий (хвилини)
(секунди), другий (хвилини)  секунд, третій (години)
секунд, третій (години) 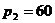 хвилини, четвертий (доба)
хвилини, четвертий (доба) 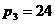 години, п’ятий (роки)
години, п’ятий (роки)  діб. Так час в три роки, 15 діб, 13 годин, 39 хвилин, 28 секунд можна визначити наступним чином:
діб. Так час в три роки, 15 діб, 13 годин, 39 хвилин, 28 секунд можна визначити наступним чином:
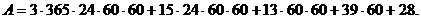
Далі будемо розглядати тільки однорідні позиційні системи числення і будемо їх називати їх просто «системи».
При записі правильних дробів позиції нумеруються в наступному порядку: -1, -2, … . При цьому ваги розрядів будуть негативними. Наприклад дріб

представляються у виді виразу
 (1.7)
(1.7)
Мішані дроби також можна представити у вигляді поліномів:
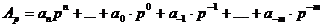 (1.8)
(1.8)
де р- основа системи числення. Вираз (1.8) відповідає лінійному запису числа А:
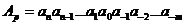
і його значення визначається за формулою:
 (1.9)
(1.9)
В табл.. 1.1. наведені вигляд перших 16 чисел в різних системах числення.
Вираз (1.9) можна використовувати для знаходження десяткових значень числа, представлених в будь-якій системі числення. При цьому степені основ визначаються за правилом десяткової системи. Наприклад, число 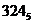 можна представити у вигляді (1.9) і знайти, що:
можна представити у вигляді (1.9) і знайти, що:
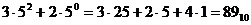
Табл. 1.1
Представлення чисел в деяких системах числення
| P=10 | P=2 | P=5 | P=8 | P=16 |
| А | ||||
| B | ||||
| C | ||||
| D | ||||
| E | ||||
| F |
Арифметичні операції в системі з основою р виконуються по правилам цієї системи. Наприклад, правила для складення (a+b) чисел в 5 системі представлені на мал.. 1.1.
На основі таблиці (1.1.(а)) можна построїти таблицю для виконання операцій множення чисел a*b (мал.. 1.2).
| bb↓ | aa→ | |||||
| bb↓ | aa→ | |||||
| -1 | ||||||
| -2 | -1 | |||||
| -3 | -2 | -1 | ||||
| -4 | -3 | -2 | -1 |
Мал. (1.1) Виконання операції додавання (а) і віднімання (б) в системі р=5
| b↓ | a→ | |||||
Мал. (1.2) Виконання операції множення в системі числення р=5
Множення а * b отримані на основі багаторазового складання, використовуючи правила, представлені на рис. 1.1 (а). Наприклад, результат множення 4 x 3 отриманий таким чином: 4+4 =13+4=10+(3+4)=10+12=22.
Правила виконання основних операцій можуть бути отримані для будь-якої системи числення. Для цього необхідно побудувати відповідні таблиці. Правила подання на рис. 1.1 і рис. 1.2 можна використовувати для додавання і множення багаторозрядних 5 чисел. Наприклад, знайдемо результат операцій (а+b), (а-b) i а х b для чисел 235 і 145 (рис. 1.3). 23
23 23 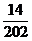
a) 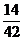 б)
б) 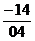 в)
в) 
Рис. 1.3. Виконання додавання (а), віднімання (6) і множення (в) для
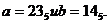
Для перевірки правильності виконання цих операцій можна виконати перевірку в десятковій арифметиці, використовуючи формулу (1.9) і правила десяткової арифметики:
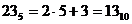


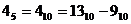

Розрахунки (1.10) підтверджують правильність результатів, наведених па мал. 1.3.
У повсякденному житті люди використовують в основному десяткову арифметику. При цьому 60 використовується для представлення часу і кутів. Знаходить застосування і 12 система. Так, на дюжини рахують посуд і олівці, а для числа 12x12 існує спеціальну назву - «грос». Проте в ЕОМ всі обчислення проводяться на підставі двійкової системи, до розгляду якої ми переходимо.
1.2. Двійкова система числення
У двійковій системі числення кожен розряд тисне приймати тільки одне з двох значень - «0» або «1». Ця одиниця інформації називається біт (від англійського «bit» - binary digit). Інформація в пам'яті ЕОМ зберігається у вигляді груп бітів, званих словами. Число біт у слові різних ЕОМ різні. Наприклад, в деяких мікроконтроллерах слово складається з чотирьох біт, у випадку ЕОМ Сгау-1 слово включає 64 біта, а в графічних процесорах - 128 біт. Група з 8 біт називається байт (byte). Команди ЕОМ і слова інформації кратні байту, тобто можуть бути довжиною 2, 4 і 8 байт. Двійкові слова можуть представляти наступну інформацію.
1. Команди ЕОМ. Команда може бути представлена у вигляді одного слова. Зв'язок між бітової рядком і операцією, що виконується ЕОМ, визначається розробником комп'ютера. Зазначимо, що команди можуть представлятися та кількома словами, що зберігаються в пам'яті ЕОМ.
2. Числа. Слова інформації можуть представляти числа, задані в деякому форматі. Наприклад, у форматі BCD 001001102 відповідає десятковому числу 26. Якщо також послідовність біт визначає ціле двійкове число, то воно відповідає числу 3810. Тут можна провести аналогію зі значенням слів у різних мовах. Наприклад, для англійців слово «gift» означає «подарунок», а для німця - «отрута».
3. Символи. У ЕОМ часто використовують операції, пов'язані з введенням або друком текстів. Відзначимо, що і програми ЕОМ вводяться у вигляді тексту. Для представлення літер, цифр і спеціальних символів (+, -, !, ?, і т.д.) використовуються двійкові коди, тому що ЕОМ може обробляти тільки їх. На практиці найбільш часто використовується семирозрядний код, званий ASCII (American Standard Code for Information Interchange).
Цей код включає 7 біт, тобто дозволяє представити 27-128 символів. З цих 128 символів 96 використовуються для друку (включаючи малі та великі символи). Решта 32 символи використовуються для символів, які не друкуються, але мають деяке спеціальне призначення, наприклад пробіл або повернення каретки друкарської машинки.
Наприклад, букві «А» відповідає код 1000001. Цей код вводиться в ЕОМ при натисканні на клавішу «А» у верхньому регістрі. Для друку літери «А» на принтер посилається код 1000001. Аналогічно, десяткові цифри від 0 до 9 представляються такими самими цифрами від 0 до 9. Таким чином, при натисканні на клавішу «2» на клавіатурі відбувається введення бітової рядка 00110010 в пам'ять ЕОМ. Очевидно, при друці символів необхідно їх коди перетворити у відповідні графічні зображення.
Для зображення символів з точками та штрихами 8-бітовий код ISO 8859-1 (Latine code). Для роботи з тисячами японських і китайських ієрогліфів використовуються Unicode, має 16 біт. Перші 256 символів цього коду відповідають ASCII. Відзначимо, що Unicode є стандартом мови JAVA.
4. Графічні елементи. Різні малюнки представляються у пам'яті ЕОМ у вигляді сукупності двійкових кодів. Існують різноманітні методи представлення графічної інформації. Наприклад, малюнок може бути параметризований і зберігатися в пам'яті як набір команд, які можуть бути використані для відновлення малюнка. У цьому випадку малюнок представляється в термінах ліній, дуг і поліномів, а також їх розташування в малюнку. Щоб надрукувати або показати малюнок на дисплеї, він відновлюється на основі своїх параметрів.
Однак більш складні малюнки представляються у вигляді бітового шаблону (bit-map). Будь-який малюнок може бути перетворений в квадратний масив елементарних зображень, званих пікселями («pixel» від англ. «Picture element»). Піксель є аналогом біта, але використовується для представлення найбільш простий інформації, з якої складається малюнок. Однак на відміну від біта піксель може мати атрибути, такі як, наприклад, колір.
Щоб збагнути складність представлення графічної інформації, розглянемо малюнок формату А4 (210x297мм). Для чіткості зображення необхідно, щоб в 1мм було близько 12 пікселів. Таким чином, один квадратний міліметр містить 12x12 = 144 пікселів, а вся картинка містить 210x297x144 = 8951040 пікселів. Це число визначає обсяг пам'яті 1 Мбайт для зберігання монохромної (чорно-білої) картинки. Якщо ж малюнок має колір, а кожен колір має 256 відтінків, то для зберігання такого малюнка потрібно 8 Мбайт. Це пояснює високу ціну графічних комп'ютерів. Відзначимо, що існують методи стиснення інформації, що представляє малюнок.
Ціле число в двійковій системі представляється у вигляді:
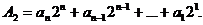 (1.11)
(1.11)
Правильна дріб має наступний вигляд:
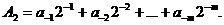 (1.12)
(1.12)
Змішаний дріб представляється наступною загальною формулою:
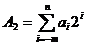 (1.13)
(1.13)
Вибір двійкової системи для ЕОМ був зроблений виходячи з аналізу таких чинників:
1. Наявність фізичних елементів, здатних зобразити символи системи. Елементи, що мають два стійких стани, є простими. До них відносять транзистори, реле, конденсатори. Цей критерій був одним з найбільш важливих для вибору двійкової системи.
2. Економічність системи, обумовлена кількістю обладнання, необхідного для подання багаторозрядних чисел і виконання операцій над ними. За цим критерієм найбільш підходить троїста система, а двійкова стоїть на другому місці.
3. Трудомісткість виконання арифметичних операцій, визначається складністю алгоритмів обробки інформації. При цьому, чим менше підставу системи, тим менше і трудомісткість.
4. Швидкодія обчислювальних пристроїв виявляється тим вище, чим менше основа системи числення. Відомо, що множення в двійковій системі виконується на 26% швидше, ніж у трійковій, і в 2,7 рази швидше, ніж у десятковій.
5. Існування формальних методів синтезу та аналізу цифрових пристроїв, що важливо для розробки схем з деякими оптимальними характеристиками. У випадку двійкової системи такий апарат є - алгебра логіки.
6. Зручність роботи людини з ЕОМ є високим лише при використанні десяткової системи. Проте дані і результат досить просто переводяться з двійкової системи в десяткову систему і навпаки.
У таблицях 1.1 - 1.3 наведені результати виконання операцій додавання, віднімання і множення відповідно для однорозрядних двійкових чисел а і b: (а+b), (a-b), а х b.
Таблиця 1.2
Двійкове складання
| b↓ | a→ | ||
Таблиця 1.3
Двійкове віднімання
| b↓ | a→ | ||
| -1 |
Таблиця 1.4
Двійкове множення
| b↓ | a→ | ||
Як видно з таблиці 1.2, при додаванні однорозрядних чисел можливий результат, що має два розряди. Таким чином, можливо переповнення розрядної сітки. Ця одиниця використовується як перенесення між сусідніми розрядами при додаванні багаторозрядних чисел (дивись §. 1.4). З таблиці. 1.3 випливає, що при вирахуванні позитивних чисел результат може бути негативним. Ця ситуація відповідає позичці одиниці зі старшого розряду числа (дивись §. 1.4). Таблиця для виконання операції ділення не приведена. Очевидно, що для а: b результат рівний а при b=1 і результат буде нескінченним при b = 0.
Фахівцям у галузі інформатики необхідно знати хоча б перші 10 ступенів числа 2. У табл. 1.5 показані ці числа для перших 16 ступенів числа 2. Крім того, дано терміни, які використовуються для назви цих чисел як масиву інформації в пам'яті ЕОМ.
Таблиця 1.5
Цілі степені числа 2
| р | 
| Термін | Р | 
| Термін |
| 1 біт | 64 байта | ||||
| півбайт | 1 к біт | ||||
| байт | 2 к біта | ||||
| 2 байта | 4 к біта | ||||
| 4 байта | 1 к байт | ||||
| 8 байтів | 2 к байта | ||||
| 16 байтів | 4 к байта | ||||
| 32 байта | 8 к байтів |
1.3. Переведення чисел з однієї позиційної системи в іншу
Це завдання постійно виникає при обробці цифрової інформації в ЕОМ. При цьому практичне значення має завдання переведення із двійкової системи в десяткову систему і навпаки. У загальному вигляді завдання переведення виглядає наступним чином.
Нехай число А представлено в системі числення з основою р1, що містить коефіцієнти 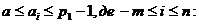
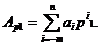 (1.14)
(1.14)
Необхідно знайти подання цього числа в системі числення з основою p2, що містить коефіцієнти 
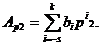 (1.15)
(1.15)
Для знаходження коефіцієнтів bi, - необхідно виконати ряд дій, заснованих на правилах арифметики в системі р1, методи перекладу цілих чисел засновані на розподілі, дробових - на множенні числа А р1 на число р1, представлене в системі р1.
Перевід цілих чисел. Ціле число 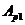 в системі
в системі  може бути записане у вигляді:
може бути записане у вигляді:
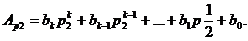
Використовуючи схему корнера (послідовне винесення р2 за дужки) можна отримати наступний вираз:
 (1.16)
(1.16)
Вираз (1.6) можна представити у вигляді:
 (1.17)
(1.17)
де значення А1 ясно з (1.16). Розділивши (1.17) на число р2, знайдемо цілу частину А1 і залишок b0, тобто молодшу цифру числа Ар2. Очевидно, залишок А1 представляється у вигляді:
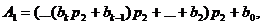 (1.18)
(1.18)
що можна представити в такій формі:
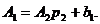 (1.19)
(1.19)
Отже, при розподілі  на число р2 отримаємо цілу частину А2 і залишок b1. Процес повторюється до тих пір, поки не буде знайдений коефіцієнт bк <р2. Це і буде старша цифра числа
на число р2 отримаємо цілу частину А2 і залишок b1. Процес повторюється до тих пір, поки не буде знайдений коефіцієнт bк <р2. Це і буде старша цифра числа  .
.
Приклад 1.1. Перекласти десяткове число А = 28 в двійкову систему числення.
Рішення: Маємо р2 =2. Виконаємо ділення в стовпчик:

Відповідь: А2=11100
Перевірка: 
Приклад 1.2. Перекласти двійкове число А2 = 1110011 в десяткову систему числення. При цьому основа р2 = 10 зображується у двійковій формі р2 = 1010.
Розв’язок:
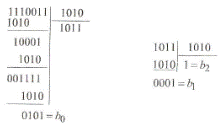
Відповідь: 
Перевірка: 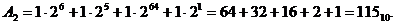
Приклад 1.3. Перевести десяткове число А10=4629 у вісімкову систему числення (р2=8).
Розв’язання:

Відповідь: А8=11025.
Перевірка: 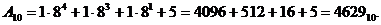
Відповімо, що для виконання останньої перевірки доцільно використовувати схему Горнера. У цьому випадку десяткове число представляється у вигляді
 (1.20)
(1.20)
Вираз (1.20) приводить до наступної схеми обчислень. Необхідно взяти старший розряд bk, помножити його па 8 і додати до результату bk-1. Цей продовження триває циклічно до додатка до b0). Перевіримо цей метод на прикладі числа 110258, що призводить до наступної послідовності дій:
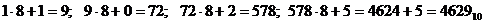
Приклад 1.4 Перевести десяткове число А=53241 в шістнадцяткову систему числення (р2=16).
Розв’язок:

Відповідь: оскільки 1510=F16, а 1210=С16, то число А10 має вигляд А10=CFF9.
Для перевірки паралельності результату використаємо вираз (1.21) замінивши в ньому 8 на 16.
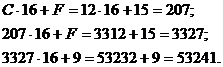
Таким чином, 5324110=CFF916.
Перевід правильних дробів. Завдання формулюється по аналогії з попереднім завданням. Нехай число А в системі р1 має вигляд
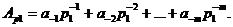
Це число необхідно представити в системі з основою р2, використовуючи коефіцієнти 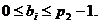 Таким чином, необхідно знайти представлення
Таким чином, необхідно знайти представлення
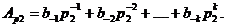 (1.21)
(1.21)
Перепишемо вираз (1.21) за схемою Горнера і отримаємо:
 (1.22)
(1.22)
З виразу (1.22) слідує метод переводу. Помножимо Ар2 на число р2 (за правилами системи р2). При цьому отримаємо результат
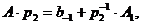 (1.23)
(1.23)
де 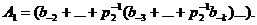 Отже, ціла частина числа (1.23) являє собою коефіцієнт
Отже, ціла частина числа (1.23) являє собою коефіцієнт 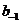 . Помножимо дріб із (1.23) на число р2 і отримаємо
. Помножимо дріб із (1.23) на число р2 і отримаємо
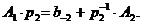
Таким чином, отриманий коефіцієнт 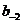 . Цей процес продовжується до тих пір, поки не будуть отримані всі коефіцієнти з (1.21).
. Цей процес продовжується до тих пір, поки не будуть отримані всі коефіцієнти з (1.21).
Трудність переводу полягає в тому, що результат перекладу може бути нескінченним. Тому переклад припиняється або при рівності дробової частини залишку виду (1.23) нулю, або при отриманні дробу з заданим числом розрядів. Природно це число визначається розрядом сітки ЕОМ.
Приклад 1.5. Перекласти А10= 0.6875 в двійкову систему числення. Рішення:
0,6875 х 2 = 1,3750, тобто 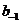 = 1;
= 1;
0,3750 x2 = 0,7500, тобто 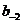 = 0;
= 0;
0,7500 х 2 = 1,5000, тобто  = 1;
= 1;
0,5000 х 2 = 1.0000, тобто 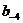 = 1.
= 1.
Так як дробова частина результат четвертого кроку обчислень дорівнює нулю, то процес закінчено. Відповідь: 0,687510 = 0,10112.
Приклад 1.6. Перекласти А2= 0.1101 в десяткову систему числення.
Рішення:
0,1101 x1010 = 1000,0010, тобто 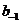 = 8;
= 8;
0,0010 x1010 = 0001,0100, тобто 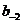 = 1;
= 1;
0,0100 x1010 = 0010,1000, тобто  = 2;
= 2;
0,1000 x1010 = 0101,0000, то єсть 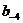 = 5.
= 5.
Так як дрібна частина результат четвертого кроку множення на число 102 = 1010 дорівнює нулю, то процес закінчено.
Відповідь: 0,11012 = 0,812510.
Перевірка: Перевірку можна виконати так, як у прикладі 1.5. Проте можна поступити наступним чином. У десятковій системі число 1 101 дорівнює 13, тобто дріб можна знайти як 13:16 0,8125. Аналогічно, в прімсрс1.5 перевірку можна провести, поділивши 11 (десятковий еквівалент числа 1011) на 16.
Приклад 1.7. Перекласти десяткову дріб А10 = 0,12 у вісімкову систему числення. Рішення:
0,12 х 8 = 0,96, тобто 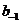 = 0;
= 0;
0,96 x8 = 7,68, тобто 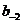 = 7;
= 7;
0.68 х 8 = 5,44, тобто  = 5;
= 5;
0,44 х 8 = 3,52, тобто 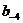 = 3.
= 3.
Відповідь: При довжині розрядної сітки чотири, маємо наступна відповідність 0,1210 = 0,07538, тобто є похибка і подання вихідної дробу, обумовлена як 0,0000418.
Приклад 1.8. Перевести А10 = 0,12 в шістнадцяткову систему з точністю до чотирьох розрядів. Рішення:
0,12 x16 = 1,92. тобто 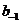 = 1;
= 1;
0,92 х 16 = 14,72, тобто 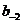 =Е;
=Е;
0,72 х 16 = 1 1,52, тобто  = В;
= В;
0,52 х 16 = 8,32, тобто 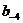 = 8.
= 8.
Відповідь: При заданій точності 0,1210 = 0,1ЕВ816.
Перевірку правильності перекладу в двох останніх прикладах ми залишаємо читачеві.
При перекладі змішаних дробів їх ціла частина перекладається методом розподілу, а старша - множення на основу р2.
Приклад 1.5. Перекласти десяткове число А10 = 28,6875 в двійкову систему числення.
Рішення: З прикладу 1.1 можемо отримати цілу частину (11100), з прикладу 1.5 маємо дробову частину (0,101 1).
Відповідь: 28,687510 = 11100,10112.
Використання проміжної системи числення. Цей підхід використовується при перекладі з двійкової системи в десяткову систему, і навпаки. Як проміжний системи використовуються вісімкова (в даний час все рідше) і шістнадцядцяткова система. Як видно з табл. 1.1, одна вісімкова цифра замінює три двійкових (тріаду), а одна шістнадцяткова - чотири (тетраду). З цієї причини числа у восьми-і шістнадцятковій системі в три і чотири рази коротше відповідно, ніж у двійковій.
В даний час 16-ричная система широко використовується для представлення чисел в комп'ютерах, а також при роздруківці вмісту пам'яті ЕОМ. Як правило, роздруківка частини пам'яті ЕОМ (соге-с1ішр) використовується при діагностиці несправностей, які неможливо знайти автоматизованими методами. Проте бувають ситуації, коли і для людини двійкова система буває більш інформативна, ніж інші.
Наприклад, нехай якийсь хімічний процес включає використання трьох нагрівачів (Н1, Н2, НЗ), трьох засувок (VI, VI, УЗ) і двох насосів (Р1, Р2.РЗ). Для управління цими пристроями використовується байт інформації. Якщо певний розряд цього байта дорівнює нулю, то відповідний йому агрегат вимкнений. Якщо цей розряд дорівнює одиниці, то - включений. Нехай розряди цього байта відповідають пристроям у наступному порядку H1, Н2, НЗ, VI, V2, V3, P1, Р2. При цьому байт 10110101 однозначно говорить про стан апаратури. При цьому інші представлення цього числа, а саме 2688, C5l6 або 9310 не дають нічого.
При перекладі числа А8 в А2 необхідно відобразити кожну вісімкову цифру у вигляді тріади. Наприклад, А8 = 3768 відповідає А2 = 111111102 (дивись табл. 1.1). При зворотному перекладі двійкове число розбивається на тріади, починаючи з правого крайнього розряду. Потім кожна тріада замінюється її восьмеричним еквівалентом. Наприклад, .А2 = 110110102 розбивається на 3 тріади 11 011 010 чому відповідає число A8 = 3328.
При перекладі числа А16 в А2 необхідно відобразити кожну 16-річную цифру у вигляді тетради. Наприклад, А16= А2В16 відповідає коду А2 = 1010001010112. При зворотному перекладі двійкове число починається з самого правого розряду, розбивається на тетради. Далі кожна тетрада замінюється своїм 16-кодовим еквівалентом. Наприклад, число А2=10101101101000112 розбивається на чотири тетради 1010 10111010 1011, які перетворюються в А16= ADA316.
1.4. Різновиди двійкових систем
Двійкова система може використовуватися для представлення десяткових чисел, причому кожна десяткова цифра кодується за допомогою чотирьох двійкових розрядів. Такі системи називаються двійково-десятковими (аналітичний варіант BCD - binary-coded decimal). Такий підхід спрощує завдання переведення чисел з десяткової системи в двійкову систему і назад. Однак, з теорії двійкової арифметики відомо, що для представлення однієї десяткової цифри досить близько 3,3 біт. Таким чином, використання двійково-десяткового арифметики веде до великої розрядності чисел, ніж при двійкової арифметики. Це в свою чергу збільшує вимоги до місткості пам'яті, що зберігає числа.
Двійково-десяткова система є прикладом кодування позиційної системи, в якій цифри однієї системи числення кодуються цифрами іншої системи. Розрізняють два підходи до кодування - з природними розрядами і з штучними вагами розрядів. Прикладом першої системи є BCD система з вагами розрядів 8 - 4 - 2 - 1, тобто  . Кодування десяткових цифр і системі 8-4 - 2-1 наведено в табл. 1.6.
. Кодування десяткових цифр і системі 8-4 - 2-1 наведено в табл. 1.6.
Таблиця 1.6
Представлення десяткових цифр
| 10 цифра | Код 8-4-2- 1 | Код2-4-2-1 | Код 8-4-2-1 +3 |
| 01 11 | |||
| б | 01 10 | ||
| 01 11 | 1 101 | ||
| 101! | |||
Системі 8 - 4 - 2 - 1 притаманний суттєвий недолік, пов'язаний з виконанням арифметичних операцій. Наприклад, 5 +7 = 12, то є перенос і результат в даному розряді дорівнює 2. При складанні ж чисел 0101 і 0111 виходить такий результат: 1100, то рівне 1210. При цьому перенесення відсутнє і його необхідно створити штучним чином, що ускладнює апаратуру суматора. Перевагою коду 8-4 - 2 - 1 є простота подання інформації.
Цього недоліку позбавлена система з вагами 2 - 4 - 2 - 1, яка належить до системи з штучними вагами розрядів. Представлення чисел у цій системі дано в табл. 1.6. Так число 146810 представляється у вигляді такої послідовності біт: 0001 0100 1100 1110. У цій системі складання 5 + 7=0101 + 1101 = 10010, тобто результат дорівнює 2. Це пов'язано з тим, що система 2-4-2-1 є самодоповняюча. Код називається самодоповняльним, якщо з рівності a10+b10 = 9 слідує рівність a2+b2 = 1111. Наприклад, 5+4 = 9, а 0101 1010 = 1111. Це спрощує проблему формування переносу між розрядами, однак пов'язана з труднощами перекладу.
Ще одним прикладом само доповняльного коду є так званий «код з надлишком 3», тобто система 8 - 4 - 2 - 1 3 (табл. 1.6). Ця система дозволяє спростити арифметичні операції, а при перекладі з десяткової системи достатньо додати до коду 8 - 4 - 2 - 1 число 3 = 0011. Очевидно, це складання уповільнює переклад чисел. Крім того, при зворотному перекладі число 3 необхідно відняти з кожної тетради коду BCD. Система 8 - 4 - 2 - 1 3 володіє не постійними вагами розрядів. Наприклад, цифра 110= 01002, то є третій розряд має вагу 1. У числі ж 910 = 110010 цей розряд має вагу 4. Відзначимо, що табл. 1.6 задає однорідні коди, тому що в кожному розряді знаходиться тільки 0 або 1.
Відомі виконавчі системи спеціального призначення, створені для прискорення обчислень в комп'ютерах. Проте всі ці системи характеризуються трудністю переведення чисел з класичних позиційних систем і назад. Тому їх застосовують тільки, якщо не потрібно змінювати систему при введенні-виведенні даних, або якщо переказ здійснюється без залучення складної апаратури.
Прикладом такої системи є врівноважена троїста система, де р = 3 і використовуються цифри 1,0,  . Число Т означає -
. Число Т означає -  . У цій системі будь дійсне число (позитивне чи негативне) уявляється без знака. Розглянемо запис деяких чисел у цій системі:
. У цій системі будь дійсне число (позитивне чи негативне) уявляється без знака. Розглянемо запис деяких чисел у цій системі:
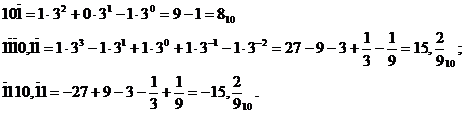
З цих прикладів видно основні переваги системи 1,0,  . а саме:
. а саме:
- Знак числа визначається його першим значущим розрядом (1-відповідає, а  - негативному числу);
- негативному числу);
- Для переходу до СОТ з протилежним знаком необхідно поміняти 1 на  і навпаки;
і навпаки;
- Для одержання цілого числа (округлення до найближчого цілого) достатньо відкинути дробову частину.
Для підсумовування багаторозрядних чисел досить знати наступні правила:
 +
+  = (-3)+ (-3) = -6 =
= (-3)+ (-3) = -6 =  1; 1+
1; 1+  = 0; 1+1 = 3+3 = 6 = 1
= 0; 1+1 = 3+3 = 6 = 1  .
.
Приклад 1.10. Знайти результат складання чисел 7+2 і 7 (-2) в системі
1.0.  .
.
Рішення: Кількість 710 = 1  1, число 210 = 01
1, число 210 = 01  , число -210 = 0
, число -210 = 0  1.
1.
 ;
; 
Віднімання в цій системі зводиться до складання з числом, яке протилежно від'ємному. Наприклад, 7 - 2 = 7 (- 2) = 1  1+0
1+0  1 = 1
1 = 1 
 (з прикладу 1.10). Для виконання множення достатньо врахувати три правила:
(з прикладу 1.10). Для виконання множення достатньо врахувати три правила:
- при множенні па 0 часткове твір дорівнює кулю;
- при множенні на «мінус 1» знак часткового твори змінюється на протилежний, що дасть негативне множеному;
- при множенні на 1 часткове твір збігається з множеними.
Приклад 1.11. Помножити числа 1910 і 3310, представлені в врівноваженій трійковій системі числення.
Рішення: 1910 = 1  01 = 3*3*3-З*3+1;
01 = 3*3*3-З*3+1;
3310 = 11  0 = 27 +9 -3;
0 = 27 +9 -3;
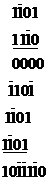
Відповідь: 
Перевірка: 33 х 19 = 627, тобто результат вірний.
Якщо числа представлені в двійковому коді, то при переході від зображення одного числа до зображення сусіднього числа може відбуватися одночасна зміна чисел у розрядах числа. Наприклад, при переході від 710 = 0111 до 810 = 1000 міняються всі чотири значення. Це може призвести до збоїв в роботі апаратури.
Для усунення цього недоліку використовується код Грея (табл. 1.7). розряди якого не мають постійної ваги. Як видно з табл. 1.7, в числі 710 одиниця третього розряду має вагу 7, а в 410 - три або один. Цей код має кілька переваг перед звичайним кодом 8 - 4 - 2 - 1, а саме:
- при послідовному переході від числа до числа міняється тільки один розряд коду;
- зміна значень кожного розряду відбувається вдвічі швидше, ніж у коді 8 - 4 - 2-1 (при послідовному переході між числами).
Ці особливості використовуються, наприклад, при побудові оптичних кодуючи пристроїв, що перетворюють кут повороту в двійковий код. Такі пристрої дозволяють вимірювати кут (знаходити кутове положення) без механічного зв'язку між валом і вимірювальним приладом. Типовий приклад використання оптичного кодера - автоматична система прогнозу погоди. Так, напрям вітру в цьому випадку визначається кутом повороту флюгера. Цей флюгер знаходиться на вагу, пов'язаним з оптичним кодером, що переводять кут повороту валу (напрямок вітру) в двійковий код.
Таблиця 1.7
Код Грея для десяткових чисел
| А10 | Код Грея | А10 | Код Грея |
| 1 101 | |||
Оптичний кодер включає пластиковий диск, покритий концентричними доріжками. На доріжках виділяються сектори, пропускаються (логічна 1) і не пропускає (логічний 0) світло. Ці доробки відповідають розрядам двійкового коду. За кожною доріжкою знаходиться джерело світла. На іншій стороні диска знаходяться фотоелектричні сенсори, по одному навпроти одного джерела світла. Якщо сенсор освітлений (прозорий сектор доріжки), то фіксується одиниця р відповідному розряді коду сектора повороту. У табл. 1.8 показані 10 помилкові кодування при розбитті диска на 8 секторів.
Фізичні елементи системи мають ряд недоліків. По-перше, фотоелектричні елементи не можуть бути встановлені абсолютно точно Проти джерел світла. По-друге, ці джерела не є точковими, їх світло розсіюється і може потрапити на дві доріжки. По-третє, кордон секторів не є ідеальними прямими. При використанні двійкового коду 421 можлива ситуації зміни декількох розрядів коду одночасно. У силу недосконалості устаткування один із розрядів може змінитися раніше іншого. Наприклад, перехід від коду 001 до коду 010 може проходити як послідовність 001, 000, 010. Якщо комбінація 000 буде зафіксована, то це може призвести до збою в роботі апаратури. При використанні коду Грея такі ситуації виключені, так як завжди змінюється тільки один розряд коду (змінюється фото проникність тільки однієї доріжки).
Таблиця 1.8
Кодування інформації в оптичному коді
| Сектор | Кут повороту | Двійковий код 421 | Код Грея |
| 0-45 | |||
| 45 - 90 | |||
| 90- 135 | |||
| 135-180 | |||
| 180-225 | |||
| 225-270 | |||
| 270-315 | |||
| 315-360 | 1 11 |
Недоліком позиційних систем числення з непостійними вагами розрядів (у тому числі і коду Грея) є трудність обробки інформації. Тому для роботи з такими кодами необхідна їх перекодування при введенні в ЕОМ і виведення з неї.
Недоліком позиційних систем числення є наявність міжрозрядних переносів (позичок) при виконанні арифметичних операцій над міжрозрядними числами. Це обмежує швидкість виконання операцій або призводить до ускладнення апаратури, тому що запроваджуються блоки прискорення операції. Цих недоліків позбавлені символічні системи числення, в яких цифри є символами, кожен з яких окремо ніяк не характеризує окреме число. Характерним прикладом символічної системи є система залишкових класів (СЗК), в якій числа представляються в залишках.
Число в СЗК зображується у вигляді залишків від ділення заданого числа А10 на ряд взаємно-простих чисел s1, s2,…,sn . При цьому утворюється число з вагами розрядів, відповідно рівним s1, s2,…,sn. Таким чином, число А10 можна представити у вигляді a1, a2,…,an , де

 (1.24)
(1.24)
Вираз (1.24), [а] означає цілу частину числа а. Це вираз покладено в основу табл. 1.9, що представляє перші 16 чисел десяткової системи в СЗК з вагами розрядів s1= 2, s2 = 3 і s3 = 5, то мережа СЗК <2, 3, 5>.
В СЗК процеси підрахунку, додавання, віднімання і множення виконуються порозрядно. Такі системи застосовуються в спеціалізованих ЕОМ зі строго фіксованим діапазоном вихідних чисел і проміжних результатів. При цьому операції поділу повинні виконуватися вкрай рідко.
Таблиця 1.9
Представлення десяткових чисел в СЗК <2, 3, 5>
| Число | 
| 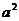
| 
| Число | 
| 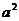
| 
|
| ¡3 | ! | з | |||||
Матеріал, розглянутий у цій главі, дозволяє привести класифікацію систем числення (мал. 1.4).
В [2] наведені корисні навички поводження з двійковими числами, які повинен вміти фахівець в області інформатики. Це такі прийоми:
1. Число 1000 ... 0 = 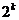 , де k- число нулів у числі. Необхідно знати на пам'ять хоча б перші дванадцять ступенів двійки (табл. 1.5).
, де k- число нулів у числі. Необхідно знати на пам'ять хоча б перші дванадцять ступенів двійки (табл. 1.5).
2. Число 11 ... 11 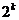 -1, де к - число одиниць у записі числа.
-1, де к - число одиниць у записі числа.
3. Необхідно знати на пам'ять десяткові значення двійкових чисел від 0 до 31. Надалі будемо їх називати «малими числами».

Мал. 1.4 Класифікація систем числення
Знаючи на пам'ять малі числа, легко перевірити правильність операції додавання (віднімання) двійкових чисел, якщо їх можна розбити на групи, не пов'язані між собою переносами (позичками).
Приклад 1.14. Необхідно перевірити результат додавання чисел А= 1011101011 і В = 10101110, рівний 1110011001.
Рішення: При складанні немає перенесення з п'ятого розряду, тобто числа можна розбити на дві групи, молодша з яких має 5 розрядів
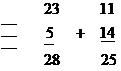
Відповідь: порівняння лівих і правих частин результату показує правильність складання.
4. Читання двійкових дробів проводиться таким чином. Розряди праворуч від коми читаються як ціле число, яке є чисельником. Знаменник дробу читається як ціле число, що є ступенем двох, показник якого дорівнює номеру молодшого розряду.
Приклад 1.15. Число А= 0,1011 =  (одинадцять шістнадцятих);
(одинадцять шістнадцятих);
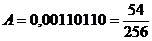 (п'ятдесят чотири двісті п'ятдесят шість)
(п'ятдесят чотири двісті п'ятдесят шість)
Дріб А = 0,00 ... 01, що включає n - 1 нулів після коми, дорівнює  . Дріб A = 0,11 ... 1, що включає n одиниць після коми, дорівнює
. Дріб A = 0,11 ... 1, що включає n одиниць після коми, дорівнює  .
.
5. Двійкові дроби можуть бути неперіодичними. Наприклад, дріб виду 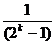 включає групу з k - 1 нулів і однієї одиниці.
включає групу з k - 1 нулів і однієї одиниці.
Аналогічно, дріб вигляду  включає групу з k одиниць.
включає групу з k одиниць.
Приклад 1.16.
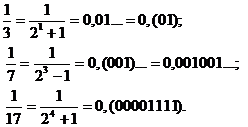
Читайте також:
- I. Органи і системи, що забезпечують функцію виділення
- I. Особливості аферентних і еферентних шляхів вегетативного і соматичного відділів нервової системи
- II. Анатомічний склад лімфатичної системи
- II. Множення круглих багатоцифрових чисел на розрядні числа.
- II. Правила щодо аргументів.
- IV. Розподіл нервової системи
- IV. Система зв’язків всередині центральної нервової системи
- IV. Філогенез кровоносної системи
- N – чисельність популяції
- POS-системи
- T. Сутність, етіологія та патогенез порушень опорно-рухової системи
- V. Етичні правила психологічних досліджень
| <== попередня сторінка | | | наступна сторінка ==> |
| | | Тема 2. Подання інформації в електронно-обчислювальних машинах. |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |