Тема 14. Синтез суматорів

Суматором називається схема, що визначає результат складання двох n- розрядних двійкових чисел S = А + В, що має n+1 розряд. Старший розряд суми називається перенесенням. Основою багаторозрядних суматорів є однорозрядні повні суматори (рис. 14.1 а), з'єднання яких (рис. 14.1 б) дає багаторозрядний суматор. Тут р- вихід перенесення, с - вхід переносу, 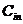- вхід переносу з попередньої секції суматора, - вихідний перенесення. Схема на рис. 14.1 б називається суматором з послідовним переносом. Це найбільш повільний з усіх можливих паралельних суматорів. Для збільшення швидкодії існують різні методи прискореного перенесення, які виходять за рамки цієї книги.

Розглянемо таблицю істинності для однорозрядного суматора (табл. 14.1) і побудуємо карти Карно для функцій S і р (рис. 14.2).

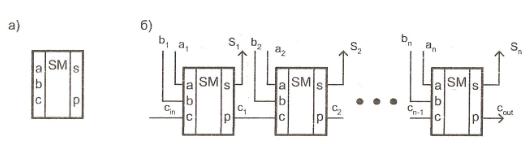
Рис. 14.1. Умовне позначення однорозрядного суматора (а) і організація багаторозрядного суматора (б)

Таблиця 14.1

Рис. 14.2. Карти Карно для однорозрядного суматора

Як видно з рис. 14.2, функція S не мінімізується, тобто

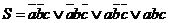. (14.1)

Функція р може бути промінімізована, що дає формулу

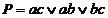. (14.2)

Застосування законів подвійної інверсії і Де Моргана до виразів (14.1) - (14.2) приводить до канонічного рівнянням схеми одно розрядного суматора:

, за яким далі будується канонічна схема (рис. 14.3).

Схема має три рівні, тобто її швидкодію 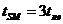, і є самою швидкодіючою з можливих варіантів. Ця схема має ряд недоліків, важливих в умовах масового виробництва:

1. Схема використовує як прямі, так і інверсні значення вхідних змінних, що призводить до великої кількості провідників. Як правило, при побудові практичних схем використовують прямі виходи регістрів

2. У схемі використовуються елементи з різним числом входів, що приводить до деяких труднощів при виготовленні шаблонів.

Так як на практиці в реальних схемах багаторозрядних суматорів використовуються різні методи прискореного перенесення, то число рівнів у схемі однорозрядного суматора не має істотного впливу на час виконання складання.

Рис. 14.3 Канонічна схема однорозрядного повного суматора

Розглянемо метод синтезу суматора, який використовується на практиці.

З аналізу табл. 14.1 випливає, що S = 1, якщо число одиниць у вхідному наборі непарне, тобто S = 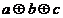. З табл. 14.1 маємо СДНФ функції

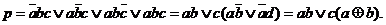
Покажемо, що Аналогічно, маємо . Тоді для функції р можна виконати наступні перетворення:

з чого випливає, що . Цей вираз показує спосіб реалізації функції , при цьому схема для функції S являє собою послідовне з'єднання схем для функцій S1= і S= S1 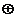С. Схема однорозрядного суматора, заснована на розглянутих перетвореннях виразів (14.1) - (14.2), наведена на рис. 14.4.

Схема на рис. 14.4 не має недоліків, властивих канонічній схемі, крім того ціна по Квайну канонічної схеми дорівнює 28, а для практичної схеми - 20, в канонічній схемі 12 вентилів, а в практичній - 10. Природньо, практична схема є більш повільною: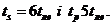

Цей приклад синтезу показує, що для досягнення заданих на практиці критеріїв часто потрібні глибокі перетворення систем булевих функцій, що описують закон функціонування комбінаційної схеми.

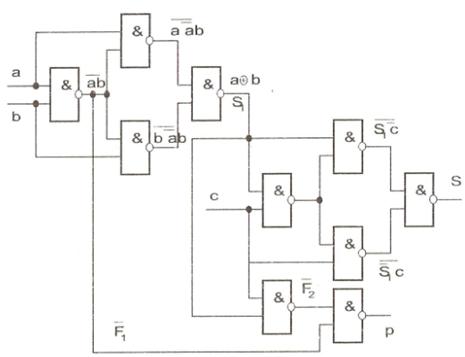
Рис. 14.4. Використовувана на практиці схема однорозрядного суматора

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
Тема 13. Синтез мультиплексора та демультиплексора	\|	Тема 15. Синтез тригерів

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.003 сек.