• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Ємнісний елемент

Ємнісний елемент – це ідеалізований елемент електричного кола, який має властивість оборотно накопичувати енергію електричного поля, а також забезпечувати протікання між своїми затискачами струму зміщення (поняття про цей струм вивчають у курсі фізики).

Типовим прикладом ємнісного елемента є плоский конденсатор, пластини якого складені з ідеального провідника, а між пластинами знаходиться вакуум.

Умовне позначення ємнісного елемента (ідеального конденсатора) наведене на рис. 4.18.

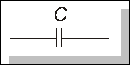
рис. 4.18

З курсу фізики відомо, що заряд q, накопичений конденсатором у деякий момент часу (тобто миттєве значення заряду), є прямо пропорційним напрузі u_С, прикладеній до конденсатора в цей момент часу (тобто – миттєвому значенню напруги на конденсаторі)

q = Cu_C.

За визначенням, миттєва величина електричного струму – це швидкість змінювання заряду:

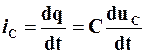. (4.9)

Звідси .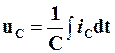

Ці формули є справедливими за будь-якого закону зміни u_С у часі.

Коефіцієнт пропорційності С називають електричною ємністюідеального конденсатора (звичайно – просто ємністю). Величину ємності вимірюють у фарадах (Ф), при цьому 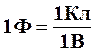.[2]

У лінійному колі величина С є постійною і визначається лише формою, геометричними розмірами та взаємним розташуванням пластин конденсатора, а також відносною діелектричною проникністю діелектрика, який заповнює простір між пластинами.

Якщо до ідеального конденсатора (рис. 4.19) прикладена синусоїдна напруга 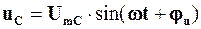, то через нього тече синусоїдний струм

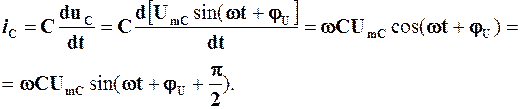(4.10)

рис. 4.19

Але з іншого боку 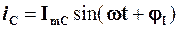. Порівнявши два останніх вирази, отримаємо, що для ідеального конденсатора

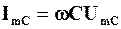(4.11)

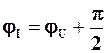(4.12)

Таким чином, напруга на ідеальному конденсаторі (ємнісному елементі) 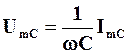прямо пропорційна силі струму крізь конденсатор, але зворотно пропорційна ємності конденсатора та частоті струму. Величину

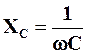
називають реактивним опором конденсатора.Він зворотно пропорційний частоті (рис. 4.20). Отже, можна записати, що

U_mC=I_mCX_C,

або для діючих значень напруги та струму:

U_C=I_CX_C.

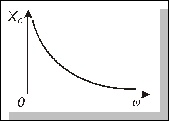
Рис. 4.20

Вираз (4.12) означає, що струм у ідеальному конденсаторі випереджає напругу за фазою на 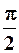(рис. 4.21).

Тепер перейдемо до символічної форми запису. Виразові (4.10) для миттєвих значень відповідає таке співвідношення між комплексною амплітудою струму 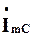та комплексною амплітудою напруги :

,

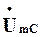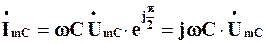звідки

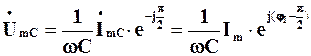. (4.13)

Відповідну векторну діаграму наведено на рис. 4.22.

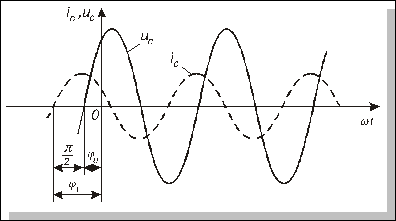
Рис. 4.21

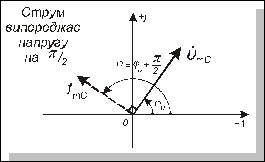
Рис. 4.22

Оскільки 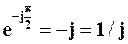, то з (4.13) отримаємо, що

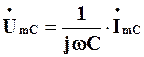. (4.14)

Величину

,

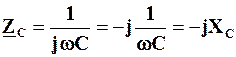яка фігурує у виразі (4.14), називають комплексним опоромідеального конденсатора (ємнісного елемента). Це чисто уявна величина. Отже, можна записати, що

,

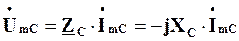або для комплексів діючих значень напруги та струму, що

.

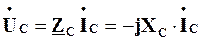Залежність Z_С(w) на комплексній площині ілюструє рис. 4.23.

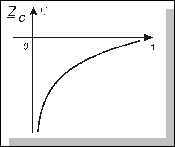
Рис. 4.23

Миттєва потужність, споживана ємнісним елементом, дорівнює:

.

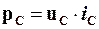Підставивши сюди вирази для миттєвих значень напруги та струму, отримаємо, що

.

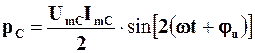Згідно з цим виразом, миттєва потужність в ємнісному елементі змінюється в часі так, як це показано на рис. 4.24.

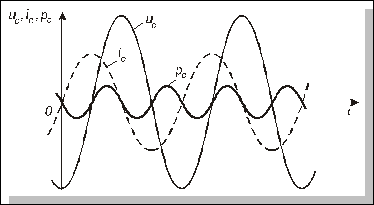
Рис. 4.24

Активна потужність є середнім за період значенням миттєвої потужності:

.

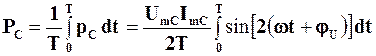Оскільки w=2p/Т, то цей інтеграл дорівнює нулю як інтеграл від синуса за час, кратний періоду. Тому активна потужність, споживана ємнісним елементом, дорівнює нулю: P_C=0.

Неважко показати, що енергія, накопичена в ємнісному елементі з моменту t=0 по деякий поточний момент часу t=t, дорівнює 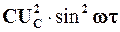. Звідси випливає, що ця енергія періодично змінюється від величини 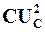в момент максимального накопичення до нуля в момент, коли ємнісний елемент повернув усю накопичену енергію в зовнішнє коло.

Завдяки своїй властивості накопичувати енергію, а потім повертати її у зовнішнє коло ідеальні котушка та конденсатор дістали назву “реактивні елементи кола”.

Читайте також:

1. I. Застосування похідної та інтеграла до роз’язування задач елементарної математики.
2. II. Елементи операційних витрат
3. II. За зміною ступенів окиснення елементів, які входять до складу реагуючих речовин
4. II.Біогеоценоз – елементарна одиниця біосфери.
5. Абетка елементів поведінки тварини
6. Аграрна структура та її елементи
7. Адвокатура — неодмінний складовий елемент механізму забезпечення прав людини.
8. Адміністративне правопорушення як підстава юридичної відповідальності: ознаки і елементи
9. Адміністративне правопорушення як підстава юридичної відповідальності: ознаки і елементи.
10. Азот, фосфор, біогенні елементи та їх сполуки, органічні речовини
11. АКУСТИКА. ЕЛЕМЕНТИ ФІЗИКИ СЛУХУ. ОСНОВИ АУДІОМЕТРІЇ
12. Аналіз витрат на підприємстві за їх елементами та статтями калькуляції.

Переглядів: 1317