
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
ТЕМА 6. Мультиколінеарність як особливий випадок моделей множинної лінійної регресії
План
1. Поняття мультиколінеарності та природа її виникнення.
2. Теоретичні і практичні наслідки мультиколінеарності.
3. Тестування наявності мультиколінеарності.
4. Способи вилучення мультиколінеарності.
1. Поняття мультиколінеарності та природа її виникнення.Мультиколінеарність означає, що в множинній регресійній моделі два або більше незалежних факторів пов‘язані між собою або мають високий ступінь кореляції.
Мультиколінеарність – це негативне явище множинного регресійного аналізу, яке не дозволяє оцінити окремий вплив кожного фактора на показник.
Про мультиколінеарність говорять, коли розглядають залежність між ціною акції, дивідендами акції та заробленим прибутком. У цьому випадку дивіденди та зароблений прибуток мають високий ступінь кореляцйї.
В економіці явище мультиколінеарності трапляється досить часто, оскільки існує глобальна тенденція одночасної зміни багатьох показників. Крім того, винекненю мультиколінеарності сприяє широке застосування в економетричних моделях лагових величин (тобто значень показника, взятих через деякий проміжок часу або із запізненням).
2. Теоретичні і практичні наслідки мультиколінеарності.Теоретичні і практичні наслідки мультиколінеарності випливають з таких властивостей:
- якщо для побудованих моделей властиве явище мультиколінеарності двох або більше факторів, то параметри цієї моделі стають невизначеними, тобто не можна знайти числове значення параметрів даної моделі;
- у випадку наявності мультиколінеарності середнє квадратичне відхилення параметрів цієї моделі прямує до нескінченості.
Теоретичні наслідки.
1. У випадку досконалої мультиколінеарності оцінки параметрів регресії будуть незмінними. Це означає, що при дослідженні кількох наборів результатів спостережень, якщо для кожного з цих наборів знайти оцінку параметрів і порахувати середні значення, то ці значення будуть наближатися до справжніх значень параметрів.
2. Мультиколінеарність не порушує властивості мінімуму дисперсій.
3.Мультиколінеарність властива лише моделям множинного регресійного аналізу.
Практичні наслідки.
1. При наявності мультиколінеарності дисперсія оцінок параметрів, обчислена за МНК, буде дуже великим значенням.
2. Набагато збільшуються всі довірчі інтервали параметрів і показника.
3.При наявності мультиколінеарності виникає явище незначимості t-статистики при перевірці суттєвості впливу на показник:
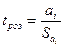 ,
,  (1).
(1).
3. Тестування наявності мультиколінеарності.На жаль не існує універсального методу який рекомендований у всіх випадках для виявлення мультиколінеарності.
У кожному конкретному випадку потрібно самостійно обирати один із відомих методів, який найбільше підходить для конкретної ситуації. Найчастіше використовють такі методи (тести) для виявлення мультиколінеарності:
1.Високе значення коефіцієнта множинної кореляції та незначимість параметрів.
2. Високе значення парних коефіцієнтів кореляції.
3. Тест Фаррара – Глаубера.
4.Характеристичне значення й умовні індекси.
Розглянемо детальніше два останні методи, які найчастіше використовують на практиці і дають найбільш достовірні результати.
Тест Фаррара – Глаубера.
Для дослідження загальної мультиколінеарності використовують метод Фаррара-Глаубера.: 1.Нормалізація змінних.
Нехай 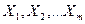 - вектори незалежних змінних. Для обчислення нормалізованих значень векторів використаємо формулу:
- вектори незалежних змінних. Для обчислення нормалізованих значень векторів використаємо формулу:
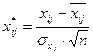 ,
, 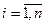 ;
; 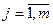 (2),
(2),
 - середнє значення вектора
- середнє значення вектора 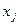 , яке обчислимо за формулою:
, яке обчислимо за формулою:
 (3),
(3),
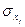 - середнє квадратичне відхилення незалежної змінної
- середнє квадратичне відхилення незалежної змінної 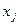 , яке обчислимо за формулою:
, яке обчислимо за формулою:
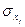 =
= 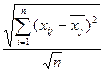
 (4).
(4).
В результаті виконання процедури нормалізації отримаємо матрицю, побудовану з нормалізованих векторів 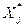 , яку позначимо через [
, яку позначимо через [ 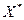 ] :
] :
 [
[ 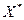 ] =
] = 
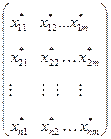 (5).
(5).
2.Розрахунок кореляційної матриці.
Взаємна кореляційна матриця обчислюється за формулою:
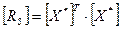 (6).
(6).
Дана матриця має розмірність 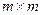 .
.
3.Обчислення значення критерію 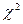 проводимо за формулою:
проводимо за формулою:
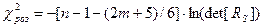 (7),
(7),
де n – кількість значень факторів;
m – кількість параметрів;
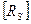 – взаємна кореляційна матриця моделі.
– взаємна кореляційна матриця моделі.
Табличне значення методу знаходимо за заданою ймовірністю р і числом ступенів вільності 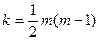 і позначаємо його
і позначаємо його 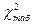 .
.
Перевіримо умову :
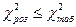 (8).
(8).
Якщо ця умова виконується, то з ймовірністю р можна стверджувати, що мультиколінеарність відсутня.
Якщо ця умова не виконується, то з ймовірністю р стверджуємо, що між деякими факторами існує мультиколінеарність. Для з’ясування між якими саме факторами існує мультиколінеарність використаємо t – статистику.
4.Визначення матриці оберненої до взаємної кореляційної 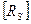 проводимо за формулою:
проводимо за формулою:
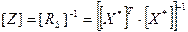 (9).
(9).
5. Обчислення значення F- критеріїв.
Для кожної незалежної величини знаходимо значення F- критеріїв за формулою:
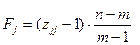 ,
, 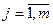 (10),
(10),
де 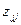 - діагональні елементи матриці [Z].
- діагональні елементи матриці [Z].
Обчислені значення порівнюємо з критичним значенням F-критерію при 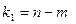 ,
, 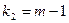 ступенями вільності і при ймовірності р. Якщо
ступенями вільності і при ймовірності р. Якщо 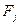 >
> 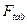 , то j-та незалежна змінна мультиколінеарна з іншими.
, то j-та незалежна змінна мультиколінеарна з іншими.
6. Знаходження часткових коефіцієнтів кореляції проводимо за формулами:
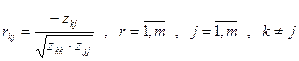 (11),
(11),
де 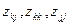 - елементи матриці [Z].
- елементи матриці [Z].
7. Для цих частинних коефіцієнтів кореляції знаходимо розрахункове значення t – статистики :
| |
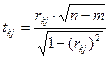 (12).
(12).
Для заданої ймовірності р і ступенів вільності 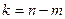 знаходимо табличне значення t – статистики tтаб і перевіряємо умову :
знаходимо табличне значення t – статистики tтаб і перевіряємо умову :
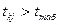 (13).
(13).
Якщо умова виконується, то з ймовірністю р стверджуємо, що між факторами 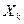 та
та  існує мультиколінеарність. Для того, щоб позбутися мультиколінеарності, використаємо найпростіший метод - метод виключення змінної. Перевіряємо, який з факторів має менший вплив на показник. Для цього знаходимо значення коефіцієнту кореляції
існує мультиколінеарність. Для того, щоб позбутися мультиколінеарності, використаємо найпростіший метод - метод виключення змінної. Перевіряємо, який з факторів має менший вплив на показник. Для цього знаходимо значення коефіцієнту кореляції 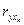 та
та 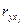 Який із цих коефіцієнтів менший, той фактор і виключаємо з моделі.
Який із цих коефіцієнтів менший, той фактор і виключаємо з моделі.
Якщо умова (13) не виконується, то між даними факторами мультиколінеарність відсутня.
.Характеристичне значення та умовний індекс. Розглядають матрицю 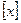 , складену зі значень факторів. Для даної матриці знаходимо власні або характеристичні числа з формули:
, складену зі значень факторів. Для даної матриці знаходимо власні або характеристичні числа з формули:
 (14),
(14),
де  - одинична матриця відповідного порядку;
- одинична матриця відповідного порядку;
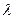 - власні або характеристичні числа матриці.
- власні або характеристичні числа матриці.
Характеристичним значенням матриці 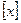 називається число:
називається число:
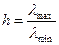 (15).
(15).
На основі величини h вводиться поняття умовного індексу: 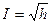 .
.
Про наявність або відсутність мультиколінеарності можна робити висновок, як за величиною характеристичного значення h, так і за величиною індексу І. Зокрема, якщо h знаходиться в межах: 100<h<1000; 10<I<30, то в цьому випадку мова йде про недосконалу мультиколінеарність.
Якщо h>1000, I>30, то мова йде про досконалу мультиколінеарність.
В інших випадках – мультиколінеарність відсутня.
4. Способи вилучення мультиколінеарності.Для усунення мультиколінеарності застосовуються такі методи:
1) метод використання первинної інформації;
2) метод об‘єднання міжгалузевої та динамічної інформації;
3) метод вилучення змінної;
4) метод перетворення змінних;
5) метод збільшення кількості спостережень.
Метод використання первинної інформації розглянемо на прикладі залежності між споживанням, доходом і багатством. Залежність між ними запишемо рівнянням:
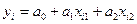 (16),
(16),
де 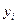 - споживання;
- споживання;
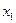 - дохід;
- дохід;
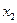 - багатство.
- багатство.
Відомо, що дохід і багатство висококолінеарні фактори. Припустимо, що між ними існує залежність, яка задається таким рівнянням: 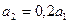 ,
,
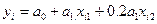 .
.
Введемо заміну змінних:
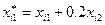 .
.
Тоді рівняння матиме вигляд:
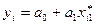 .
.
Останнє рівняння – це рівняння класу парних лінійних регресій. Можна знайти параметри 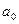 і
і 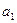 . Відповідно знайти
. Відповідно знайти 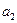 , використовуючи первину інформацію.
, використовуючи первину інформацію.
Зауваження: спрощену модель обов‘язково потрібно перевіряти на адекватність експериментальним даним.
Метод об‘єднання міжгалузевої та динамічної інформації. Розглянемо другий метод на прикладі залежності попиту на автомобілі від середньої ціни і доходу. Ця залежність описується рівнянням:
 (17),
(17),
 - кількість проданих автомобілів,
- кількість проданих автомобілів,
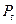 - середня ціна за автомобіль,
- середня ціна за автомобіль,
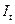 - дохід,
- дохід,
 - фактор часу.
- фактор часу.
В цьому випадку висококолінеарними є Р та І . Розв‘язання цієї задачі було запропоновано російським вченим Тобіним.Воно можливе лише за умови, коли ми розглядаємо мілігалузеву інформацію, тоді в умовах сталого доходу загалом по Україні ціна буде змінюватися не суттєво і можна ввести таку заміну змінних:
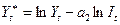 . (18).
. (18).
Тоді модель (17) набуде вигляду:
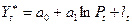 . (19).
. (19).
Рівняння (19) при сталому значенні t є квазілінійним і зводиться до лінійного шляхом заміни змінних:
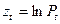 ,
,
 .
.
При кожному t=const можемо знайти а0, а1, а2 .
Зауваження. При використанні цього методу обов‘язково перевіряти модель на адекватність експериментальним даним.
Методи вилучення змінної. Суть методу полягає в тому, що з моделі вилучаємо одну із мультиколінеарних змінних, а саме ту, яка має менший вплив на показник. Вплив фактора на показник досліджуємо за допомогою лінійного коефіцієнта кореляції.
Зауваження. При застосуванні цього методу може виникнути проблема помилки специфікації, тобто, побудована модель не буде відповідати ні реальній ситуації, ні поставленому завданню дослідження залежності між показником та всіма заданими факторами.
4). Метод перетворення змінних. Цей метод найчастіше застосовується для динамічних моделей, коли показник і фактори залежать від часу. Розглянемо застосування методу на прикладі такої динамічної моделі:
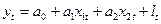 (20).
(20).
Припускаємо, що ця залежність зберігається і для моменту часу t-1
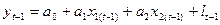 (21).
(21).
Розглянемо різницю рівнянь (20) і (21):
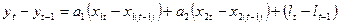 (22).
(22).
(22) – рівняння перших різниць.
Для розв‘зання цього рівняння вводять заміну зміних:
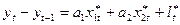 (23).
(23).
Зауваження. При використанні цього методу виникає проблема з відхиленням, оскільки воно може не задовільнити припущення моделей МЛР.
5). Метод збільшення кількості спостережень. Цей метод використовується тоді, коли є додаткова інформація про фактори та показники. Суть методу грунтується на тому, що при збільшені кількості спостережень зменшуються значення дисперсій параметрів, що дозволяє оцінити їх із більшою точністю.
Читайте також:
- Алгоритм реалізації моделей
- АНАЛІЗ ЛІНІЙНИХ МОДЕЛЕЙ ЕКОНОМІЧНИХ ЗАДАЧ
- Аналіз та синтез моделей систем
- Атестація як особливий метод оцінки персоналу
- Багатомірна лінійна модель регресії.
- Вибір моделей.
- Вибіркову (емпіричну)модель парної лінійної регресії
- Види та призначення геометричних моделей
- Визначати ступінь відповідності обраної регресії відображуваним на діаграмі даним.
- Визначення коефіцієнтів рівнянь лінійної регресії для багатофакторної задачі
- Визначення поняття системи. Економічна система як особливий клас систем
- Виконання лінійної регресії за допомогою функцій Excel
| <== попередня сторінка | | | наступна сторінка ==> |
| ТЕМА 5. Множинна лінійна регресія | | | ТЕМА 7. Гетероскедастичність як особливий випадок моделі множинної лінійної регресії |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |