
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
ТЕМА 5. Множинна лінійна регресія
План
1. Модель множинної лінійної регресії (загальний вигляд, класичні припущення).
2. Розрахунок параметрів моделі МЛР методом МНК.
3. Знаходження довірчих інтервалів параметрів та розрахункових значень показника.
4. Перевірка моделі МЛР на адекватність експериментальним даним.
5. Прогноз показника та його довірчий інтервал.
6. Виробничі функції.
6.1.Поняття та приклади виробничих функцій
6.2.Виробнича функція Кобба-Дугласа
1. Модель множинної лінійної регресії (загальний вигляд, класичні припущення).Бурхливий розвиток та широке застосування обчислювальної техніки з використанням математичних моделей дозволяють швидко провести аналіз господарської діяльності та прийняти правильне рішення, яке дозволить оптимально розподілити матеріальні, трудові та фінансові ресурси в економіці та повніше уявити економічну ситуацію, що склалася на даний час. Зрозуміло, що всі процеси мають розглядатись у взаємозв’язку.
Явище, яке залежить від багатьох факторів можна описати за допомогою множинної регресії. Дослідивши взаємозв’язок процесів у минулому і отримавши функціональний зв’язок між ними, можна з певною ймовірністю планувати майбутнє.
У процесі вивчення цієї теми студент повинен навчитись будувати моделі множинної лінійної регресії, перевіряти її на мультиколінеарність, досліджувати модель на адекватність ескериментальним даним, знаходити довірчі інтервали параметрів і розрахункових значень показника, а також прогнозувати за множинною лінійною регресією.
Розглянемо поняття множинної лінійної регресії.
Припускаємо, що між групою незалежних факторів 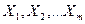 і показником Y існує лінійний зв’язок, який можна представити у вигляді :
і показником Y існує лінійний зв’язок, який можна представити у вигляді :
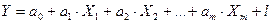 (1),
(1),
або в матричній формі
 , де (2),
, де (2),
 ;
; 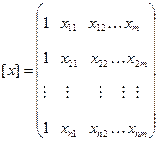 ;
;
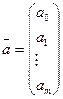 ;
; 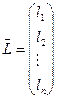 ;
; 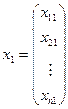 ,
,
де 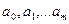 - параметри регресії (2.1);
- параметри регресії (2.1);
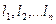 - відхилення фактичних значень показника
- відхилення фактичних значень показника 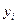 від розрахункових
від розрахункових 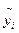 ;
;
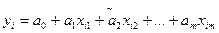 (3).
(3).
2. Розрахунок параметрів моделі МЛР методом МНК.Числові значення параметрів моделі МЛР можна обчислити за методом найменших квадратів. Враховуючи формулу (3), запишемо функціонал методу за формулою (4):
 Суть методу полягає в тому, щоб знайти такі числові значення параметрів
Суть методу полягає в тому, щоб знайти такі числові значення параметрів 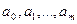 , при яких функціонал буде приймати найменше значення. Виходячи з умови існування мінімума функції багатьох змінних, запишемо систему нормальних рівнянь (5):
, при яких функціонал буде приймати найменше значення. Виходячи з умови існування мінімума функції багатьох змінних, запишемо систему нормальних рівнянь (5):
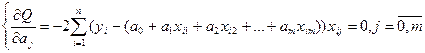 .
.
Спростимо вираз системи (5):
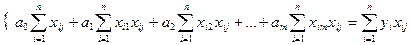 ,
,
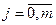 .
.
Запишемо систему (5) у розгорнотому вигляді:
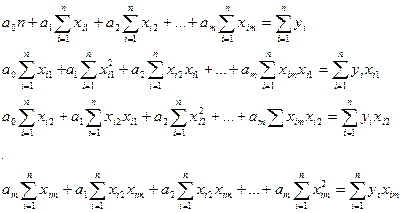 (6).
(6).
Отже, (6) – це система нормальних рівнянь функціонала (4) методу найменших квадратів. Розв’язавши цю систему методом звичайних жорданових виключень (ЗЖВ) або симплекс-методом, знайдемо числові значення параметрів 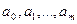 .
.
Якщо для розвязання системи (6) використовувати метод ЗЖВ, то її розвязок можна записати у такому вигляді:
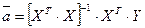 (7),
(7),
де  - це матриця, транспонована до матриці Х;
- це матриця, транспонована до матриці Х;
 - це матриця, обернена до матриці
- це матриця, обернена до матриці 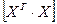 .
.
Для спрощення формули вводимо позначення  .
.
У випадку лінійної форми зв’язку коефіцієнт граничної продуктивності збігається з відповідним оціненим значенням, тобто:
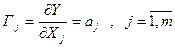 (8).
(8).
Так, наприклад, для нашої моделі (2.3) 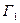 =
= 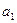 , яка означає, що при збільшенні фактора
, яка означає, що при збільшенні фактора  на 1 тисячу гривень, показник Y зросте на величину
на 1 тисячу гривень, показник Y зросте на величину 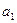 тисяч гривень.
тисяч гривень.
Коефіцієнт еластичності знаходимо з формули:
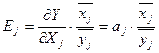 (9).
(9).
Це означає, що зі збільшенням значення фактора  на 1% , значення показника Y збільшиться на
на 1% , значення показника Y збільшиться на  %.
%.
Під час знаходження вектора 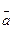 зручно використовувати електронні таблиці Excel.
зручно використовувати електронні таблиці Excel.
3. Знаходження довірчих інтервалів параметрів і розрахункових значень показника. Відхилення параметрів множинної лінійної регресії знаходимо за формулою :
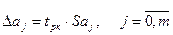 (10), де
(10), де 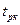 - табличне значення t – статистики Стьюдента за величиною ймовірності р і ступенями вільності
- табличне значення t – статистики Стьюдента за величиною ймовірності р і ступенями вільності  ,
, 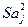 - оцінка дисперсії параметра
- оцінка дисперсії параметра 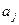 , яке знаходиться за формулою :
, яке знаходиться за формулою :
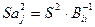 (11),
(11),
де S2 – неусувна і обґрунтована оцінка дисперсії відхилень фактичних даних від теоретичних, яке знаходиться за формулою :
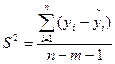 (12),
(12),
або 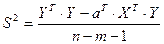 (13),
(13),
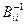 - діагональний елемент матриці
- діагональний елемент матриці 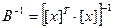 . Тоді довірчий інтервал параметра
. Тоді довірчий інтервал параметра 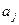 буде мати вигляд:
буде мати вигляд:
| |
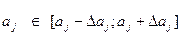 (14).
(14).
Знайдемо відносний показник розсіювання, як відношення стандартної помилки оцінки параметра до абсолютного значення параметра за формулою:
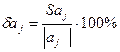 (15).
(15).
Він характеризує, наскільки вдало обчислена оцінка кожного параметра. Якщо значення 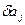 малі, то це вказує на незміщеність оцінок параметрів. І, навпаки, чим вища відносна стандартна помилка оцінки параметра, тим більше оцінена величина відрізняється від сукупності значень залежної змінної, і тим менш надійні оцінки прогнозу, розраховані з допомогою даної моделі.
малі, то це вказує на незміщеність оцінок параметрів. І, навпаки, чим вища відносна стандартна помилка оцінки параметра, тим більше оцінена величина відрізняється від сукупності значень залежної змінної, і тим менш надійні оцінки прогнозу, розраховані з допомогою даної моделі.
Для перевірки суттєвості впливу деякого фактора на показник та значущості оцінок параметрів розраховуємо величину :
 (16).
(16).
Табличне значення t – статистики tрк знаходимо за величиною ймовірності Р, та ступенем вільності  . Порівняємо значення
. Порівняємо значення 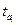 та
та 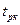 .
.
Якщо 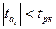 , то з ймовірністю р стверджуємо, що фактор
, то з ймовірністю р стверджуємо, що фактор  несуттєво впливає на показник Y, і його можна виключити з рівняння регресії. Інакше, рівняння множинної лінійної регресії залишаємо без змін.
несуттєво впливає на показник Y, і його можна виключити з рівняння регресії. Інакше, рівняння множинної лінійної регресії залишаємо без змін.
4. Перевірка моделі множинної лінійної регресії на адекватність експериментальним даним.Перевірка моделі множинної лінійної регресії на адекватність експериментальним даним здійснюється за допомогою критерію Фішера, розрахункове значення якого знаходимо за формулою :
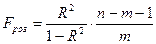 (17),
(17),
або 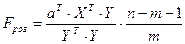 (18),
(18),
де R2 – коефіцієнт множинної детермінації, який визначається за формулою :
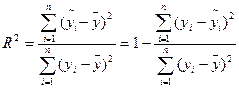 (19).
(19).
Табличне значення критерію Фішера Fтаб знаходимо за величиною ймовірності р і ступенями вільності k1=m , k2=n-m-1. Перевіряємо умову :
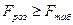 (20).
(20).
Якщо ця умова виконується, то з ймовірністю р стверджуємо, що побудована модель множинної лінійної регресії адекватна експериментальним даним і придатна для економічного аналізу та прогнозування.
Якщо умова (20) не виконується, побудована модель множинної лінійної регресії неадекватна експериментальним даним і непридатна для економічного аналізу і прогнозування.
5. Прогноз показника та його довірчий інтервал.Відхилення розрахункових значень показника знаходимо за формулою:
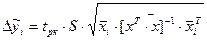 (21),
(21),
де tpк – табличне значення t – статистики за ймовірністю р та ступенем вільності  ;
;
| |
 - стовпчик, отриманий шляхом транспонування і-ої стрічки матриці [x], складений зі значень фактора хі.
- стовпчик, отриманий шляхом транспонування і-ої стрічки матриці [x], складений зі значень фактора хі.
Довірчий інтервал розрахункового значення показника буде задаватись формулою :
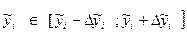 ,
, 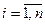 (22).
(22).
Якщо задані прогнозні значення факторів моделі множинної лінійної регресії 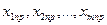 , то прогнозне значення показника
, то прогнозне значення показника 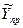 буде знаходитися за формулою :
буде знаходитися за формулою :
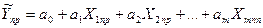 (23).
(23).
Довірчий інтервал прогнозного значення показника 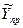 задається формулою :
задається формулою :
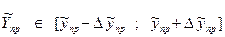 (24),
(24),
де відхилення прогнозного значення показника знаходимо за формулою :
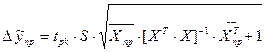 (25),
(25),
де 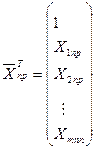 - стовпчик, отриманий шляхом транспонування стрічки матриці [x], складеної із прогнозних значень фактора хі.
- стовпчик, отриманий шляхом транспонування стрічки матриці [x], складеної із прогнозних значень фактора хі.
6. Виробничі функції. 6.1.Поняття та приклади виробничих функцій.У сфері виробництва при аналізі кількісного співвідношення показника і факторів у ролі показника можуть виступати: обсяг випущеної продукції, прибуток, товарообіг, рентабельність, собівартість одиниці продукції, фондовіддача тощо. Факторами для цих показників можуть бути: робоча сила, основні засоби або капітал, земля та її надра, продуктивність суспільної праці, рівень розвитку науки, техніки, освіти тощо.
При побудові і використанні моделі виробничої регресії результати обсягу виробництва згладжуються, водночас побудована модель дає можливість зробити якісний аналіз виробництва в цілому.
Виробнича функція – це функція, незалежна змінна якої приймає значення об’єму ресурсу, який використовується, а залежна змінна – значення об’ємів продукції, яка виготовляється.
Виробничі функції охоплюють моделювання залежностей, існуючих між такими показниками виробничої діяльності, як об’єм випущеної продукції, собівартість одиниці продукції, капітальні витрати, фондовіддача, продуктивність праці тощо.
Залежно від кількості факторів, включених в модель, розрізняють однофакторні та багатофакторні виробничі функції (ВФ).
В загальному вигляді однофакторна ВФ зображується у вигляді :
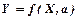 ,
,
де а – вектор параметрів ВФ;
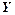 - незалежна змінна, яка відображає різні фактори виробництва (затрати праці, засобів виробництва тощо).
- незалежна змінна, яка відображає різні фактори виробництва (затрати праці, засобів виробництва тощо).
 - залежна змінна (випуск продукції, чистий дохід, ВВП тощо).
- залежна змінна (випуск продукції, чистий дохід, ВВП тощо).
Багатофакторна ВФ може бути зображена у вигляді :
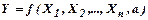 ,
,
де а – вектор параметрів ВФ;
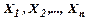 - незалежні змінні, які відображають різні фактори виробництва (затрати праці, засобів виробництва тощо),
- незалежні змінні, які відображають різні фактори виробництва (затрати праці, засобів виробництва тощо),
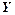 - залежні змінні (випуск продукції, чистий дохід, ВВП тощо).
- залежні змінні (випуск продукції, чистий дохід, ВВП тощо).
ВФ широко застосовується для аналізу і прогнозування економічних явищ як на мікроекономічному рівні (для підприємств, фірм, галузей, виробничих комплексів), так і на макроекономічному рівні (для регіону, країни в цілому).
На мікроекономічному рівні витрати і випуск вимірюється, як правило, у вартісних показниках і виступають вартісними агрегатами, тобто, сумарними величинами добутків об’ємів використаних ресурсів і випущеної продукції на їх ціни.
ВФ 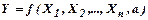 називається статичною, якщо параметри і значення результативної змінної не залежать від часу.
називається статичною, якщо параметри і значення результативної змінної не залежать від часу.
ВФ 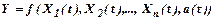 називається динамічною оскільки її параметри і значення результативної змінної залежать від фактора часу, який включається в цю модель як самостійна величина.
називається динамічною оскільки її параметри і значення результативної змінної залежать від фактора часу, який включається в цю модель як самостійна величина.
Вибір аналітичної форми виробничої функції диктується насамперед теоретичними міркуваннями, які повинні явно (або неявно) враховувати особливості взаємозв’язків між конкретними ресурсами (на мікроекономічному рівні) або економічних залежностей (на макроекономічному рівні), особливості реальних абоекспериментальних даних, що перетворюються в параметри ВФ. Зауважимо, що оцінка
| |
Розглянемо приклади найпоширеніших виробничих функцій.
1. Для характеристики залежності між податковою ставкою та обсягом податкових надходжень використовують функцію Лаффера, яка задається формулою:
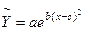 ,
, 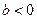 (26),
(26),
| |
де 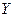 - обсяг податкових надходжень;
- обсяг податкових надходжень;
Х – значення податкової ставки;
a, b, c – параметри виробничої функції.
Графік функції Лаффера має такий вигляд :
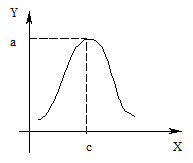
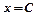 - оптимальний розмір податкової ставки, якому відповідає максимальне значення об’єму податкових надходжень. При відхиленні податкової ставки від оптимального значення вліво чи вправо значення об’єму податкових надходжень різко зменшується.
- оптимальний розмір податкової ставки, якому відповідає максимальне значення об’єму податкових надходжень. При відхиленні податкової ставки від оптимального значення вліво чи вправо значення об’єму податкових надходжень різко зменшується.
2. Для аналізу індивідуального ринку використовують виробничу функцію попиту.
Вводимо гіпотезу, що між ціною P та величиною попиту D існує стохастична залежність:
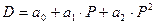 (27),
(27),
де  - невідомі параметри регресії.
- невідомі параметри регресії.
Потрібно відрізняти стохастичну залежність від функціональної. При стохастичній залежності одному значенню фактора може відповідати декілька значень показника, тоді як при функціональній залежності одному значенню аргумента відповідає лишу одне значення функції, тобто між аргументом і функцією існує взаємооднозначна відповідність.
Для регресії у вигляді многочлена другого ступеня система нормальних рівнянь має такий вигляд:
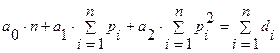 ,
,
 , (28).
, (28).
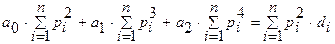
Розв’язавши цю систему рівнянь симплекс-методом або ЗЖВ, отримаємо оцінки параметрів регресії попиту. Для розв’язання системи нормальних рівнянь можна використати звичайні жорданові виключення (ЗЖВ), вибираючи за розв’язувальні елементи діагональні елементи. Нагадаємо процедуру обчислення одного кроку ЗЖВ для розв’язувального елемента 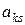 :
:
1) розв’язувальний елемент 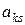 замінюється одиницею;
замінюється одиницею;
2) решта елементів розв’язувального 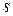 -стовпця залишається без змін;
-стовпця залишається без змін;
3) решта елементів розв’язувального 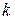 -рядка змінюють лише знаки;
-рядка змінюють лише знаки;
4) елементи, які не належать до розв’язувальних рядків і стовпців, визначаються за правилом прямокутника:
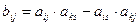 , де
, де 
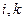 - рядки;
- рядки; 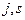 -стовпці;
-стовпці;
5) всі елементи нової таблиці діляться на розв’язувальний елемент.
Для визначення адекватності прийнятої економетричної моделі експериментальним даним скористаємось 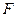 -критерієм Фішера, який полягає в наступному.
-критерієм Фішера, який полягає в наступному.
Розраховуємо значення критерію за формулою:
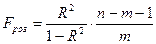 (29).
(29).
Знаходимо табличне значення 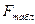 за заданою ймовірністю
за заданою ймовірністю 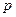 та числом ступенів вільності
та числом ступенів вільності 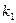 і
і 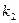 , які визначаються за формулами:
, які визначаються за формулами:
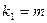 ,
, 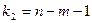 (30),
(30),
де 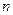 - кількість проведених спостережень;
- кількість проведених спостережень; 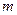 - кількість факторів, які мають суттєвий вплив на показник.
- кількість факторів, які мають суттєвий вплив на показник.
Якщо розрахункове значення більше за табличне:
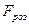 >
> 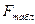 (31),
(31),
то прийнята економетрична модель вважається адекватною експериментальним даним і для неї справедливі всі закономірності функціонування і розвитку, які характерні для реального економічного явища. Тобто її можна використовувати для аналізу та прогнозування індивідуальних ринків.
Нехай відома регресія попиту 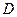 на певний вид товару як функція від ціни товару
на певний вид товару як функція від ціни товару 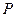 :
: 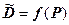 . Тоді товарообіг
. Тоді товарообіг 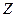 у грошовому виразі дорівнює добутку реалізованого попиту на ціну товару:
у грошовому виразі дорівнює добутку реалізованого попиту на ціну товару:
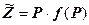 (32).
(32).
Виробника цікавлять зміни товарообігу в грошовому виразі залежно від зміни ціни на даний товар. Проведемо дослідження зміни товарообігу 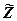 залежно від значень
залежно від значень 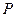 , тобто знайдемо проміжки зростання, спадання і точку екстремуму товарообігу
, тобто знайдемо проміжки зростання, спадання і точку екстремуму товарообігу 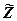 . Для цього знайдемо похідну від
. Для цього знайдемо похідну від 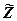 по
по 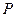 :
:
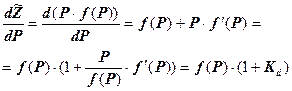 (33),
(33),
де  - коефіцієнт еластичності попиту.
- коефіцієнт еластичності попиту.
Отже, товарообіг 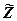 є функцією від коефіцієнта еластичності попиту
є функцією від коефіцієнта еластичності попиту 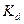 . Залежноі від знака
. Залежноі від знака 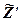 розрізняють три різних варіанти еластичності попиту:
розрізняють три різних варіанти еластичності попиту:
1. Якщо похідна від товарообігу по ціні додатна  >0, то при зростанні ціни Р зростає товарообіг
>0, то при зростанні ціни Р зростає товарообіг 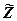 . Оскільки з економічного змісту f(P)>0, то
. Оскільки з економічного змісту f(P)>0, то  буде більше нуля, якщо
буде більше нуля, якщо 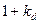 >0. Звідси випливає, що на проміжку, де товарообіг зростає, коефіцієнт еластичності попиту
>0. Звідси випливає, що на проміжку, де товарообіг зростає, коефіцієнт еластичності попиту 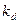 >-1. З іншого боку, регресія попиту спадна і тому
>-1. З іншого боку, регресія попиту спадна і тому 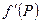 <0, тобто
<0, тобто 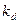 <0.
<0.
Таким чином, на проміжку зростання товарообігу коефіцієнт еластичності попиту змінюється в межах від -1до 0 (рис 1).
В економіці прийнято називати попит нееластичним, якщо коефіцієнт еластичності попиту змінюється в межах від -1 до 0.
Економічна інтерпретація. Зміна ціни на 1% викликає зміну попиту в зворотному напрямку на  %, де -1<
%, де -1< 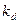 <0, при цьому товарообіг у грошовому виразі зростає.
<0, при цьому товарообіг у грошовому виразі зростає.
2. Якщо 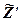 <0, то з підвищенням ціни на товар відбувається зниження товарообігу в грошовому виразі. Оскільки
<0, то з підвищенням ціни на товар відбувається зниження товарообігу в грошовому виразі. Оскільки 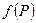 [
[ 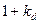 ] < 0, а
] < 0, а 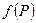 >0, то
>0, то 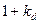 <0. Звідси випливає, що
<0. Звідси випливає, що 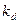 <-1.
<-1.
Якщо значення коефіцієнта еластичності попиту для даної ціни P менше –1, то попит при цій ціні еластичний.
Економічна інтерпретація. При еластичному попиті зміна ціни товару на 1% викликає зміну попиту в зворотному напрямку на 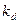 %, де
%, де 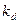 <-1. При цьому товарообіг у грошовому виразі зі зростанням ціни спадає.
<-1. При цьому товарообіг у грошовому виразі зі зростанням ціни спадає.
3. Якщо 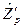 =0 для деякого проміжку цін, то на цьому проміжку товарообіг залишається сталим.
=0 для деякого проміжку цін, то на цьому проміжку товарообіг залишається сталим.
Якщо в деякій точці 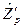 =0, то ця точка називається критичною. Причому якщо при переході через цю точку похідна
=0, то ця точка називається критичною. Причому якщо при переході через цю точку похідна 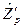 змінює знак з плюса на мінус, то при цій ціні товарообіг у грошовому виразі буде максимальним. Коефіцієнт еластичності в цій точці дорівнює -1.
змінює знак з плюса на мінус, то при цій ціні товарообіг у грошовому виразі буде максимальним. Коефіцієнт еластичності в цій точці дорівнює -1.
Визначимо проміжки зростання та спадання товарообігу. Якщо регресія попиту має вигляд многочлена другого порядку 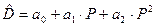 , то товарообіг для цієї регресії має вигляд:
, то товарообіг для цієї регресії має вигляд:
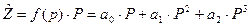 (34).
(34).
Знайдемо похідну від товарообігу за ціною:
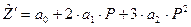 (35).
(35).
З необхідної умови екстремуму 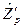 =0 знайдемо критичні точки:
=0 знайдемо критичні точки:
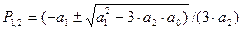 (36).
(36).
Приведене рівняння можна отримати з умови 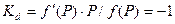 .
.
Знайдемо залежність еластичності попиту від ціни:
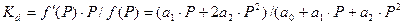 (37).
(37).
Розглянемо порядок визначення максимального прибутку. Нехай собівартість продукції складається зі сталих затрат С та змінних затрат, пропорційних обсягу випуску продукції VD. У цьому випадку прибуток підприємства буде дорівнювати різниці між товарообігом у грошовому виразі і собівартістю продукції, тобто:
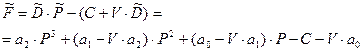 (38).
(38).
Знайдемо оцінку ціни, при якій прибуток буде максимальним. Якщо в деякій точці F досягає екстремуму, то в цій точці похідна дорівнює нулю. Знайдемо критичні точки:
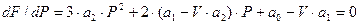 (39),
(39),
тобто отримаємо квадратне рівняння:
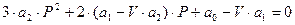 (40).
(40).
Звідси отримаємо:
 (41),
(41),
де 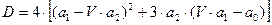 . (42).
. (42).
Точку екстремуму знаходимо, дослідивши регресію товарообігу. Припустимо, що це буде значення  , тоді оптимальна кількість продукції, що випускається, визначається за формулою:
, тоді оптимальна кількість продукції, що випускається, визначається за формулою:
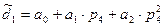 , (43)
, (43)
а максимальний прибуток за:
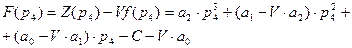 (44).
(44).
Наведену методику дослідження індивідуального ринку можна застосувати для залежності товарообігу від собівартості, яка має складніший характер.
У такому випадку для знаходження екстремальних точок необхідно застосовувати чисельні методи розв’язування рівнянь.
Якщо відомі параметри ВФ попиту, то можна розглянути функцію товарообігу:
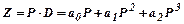 (45).
(45).
Досліджуючи дані функції, можна знайти ціну, яка відповідає найбільшому попиту та ціну, яка відповідає найбільшому прибутку.
6. 2. Виробнича функція Кобба-Дугласа.Виробнича функція Кобба-Дугласа задається формулою :
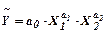 (46),
(46),
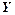 - випуск валової продукції;
- випуск валової продукції;
 - затрати праці;
- затрати праці;
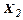 - основні фонди;
- основні фонди;
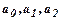 - параметри регресії.
- параметри регресії.
Виведемо формули для знаходження параметрів ВФ Кобба-Дугласа. Прологарифмуємо вираз функції :
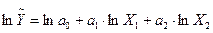 .
.
Введемо замінну змінних :
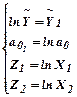 .
.
Отримаємо множинну лінійну регресію виду :
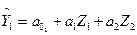 (47).
(47).
Запишемо систему нормальних рівнянь для даної моделі множинної лінійної регресії:
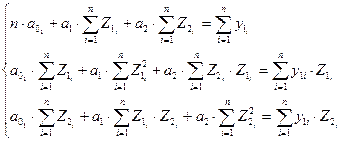 (48).
(48).
Розв’язавши систему симплекс-методом або ЗЖВ, знайдемо параметри ВФ Кобба-Дугласа. Якщо побудована модель адекватна, то її можна використовувати для аналізу та прогнозування макроекономічних явищ.
На основі ВФ Кобба-Дугласа можна визначити ряд важливих характеристик.
1. Середня продуктивність праці, яка показує середню кількість продукції на одиницю витраченого часу:
 (49).
(49).
2. Гранична продуктивність праці, яка показує, скільки додаткових одиниць продукції приносить додаткова одиниця затраченої праці.
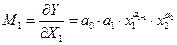 (50).
(50).
3. Еластичність випуску продукції за затратами праці, яка показує на скільки відсотків збільшується випуск продукції при збільшенні затрат праці на 1%.
| |
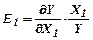 ;
; 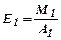 ;
;  (51).
(51).
4. Середня фондовіддача (капіталовіддача), яка показує об’єм продукції в розрахунку на одиницю використаних виробничих фондів :
 (52).
(52).
5. Гранична фондовіддача, яка показує скільки додаткових одиниць продукції приносить додаткова одиниця основних фондів :
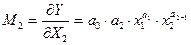 (53).
(53).
6. Еластичність випуску продукції за об’ємом виробничих фондів, яка показує, на скільки процентів збільшується випуск продукції при збільшенні основних фондів на 1%:
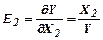 ;
; 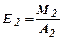 ;
; 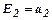 (54).
(54).
7. Сумарна еластичність за витратами (праці і капіталу), яка показує ефект одночасного пропорційного збільшення об’ємів ресурсів праці та основних фондів:
 (55).
(55).
8. Фондоозброєність (капіталоозброєність) праці :
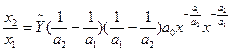 (56).
(56).
ВФ дозволяє розраховувати потребу в одному з ресурсів при заданому об’ємі виробництва та величині другого ресурсу.
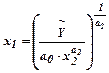
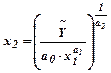 .
.
Гранична норма заміни i-ого ресурсу j-им ресурсом позначається :
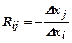 ;
; 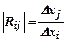 (57).
(57).
| |
Для двохфакторної ВФ Кобба-Дугласа справедливо :
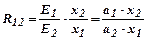 (58).
(58).
Еластичність заміщення ресурсів має вигляд :
 (59).
(59).
Вона показує, на скільки відсотків повинно змінитися відношення ресурсів (при фіксованому випуску продукції), щоб гранична норма заміщення Rijзмінилася на 1%.
Розглянемо геометричну інтерпретацію основних характеристик ВФ Кобба-Дугласа.
Виробничу функцію Кобба-Дугласа геометрично можна зобразити як поверхню в тримірному просторі з координатами х1, х2,у.
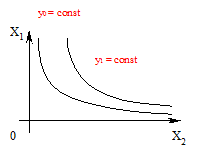
Для цієї регресії геометричне місце точок функції рівнянь х1і х2, для яких показник виробництва обсягу продукції у є сталим, називається ізоквантною.
Запишемо рівняння ізокванти для деякого значення 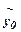 :
:
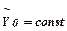
 |
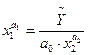 ;
; 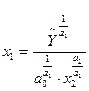 ;
; 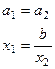 .
.
Якщо розглянути виробничу функцію Кобба-Дугласа при сталих обсягах капіталу, то отримаємо залежності:
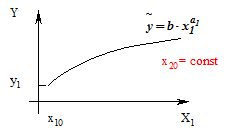
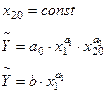
Якщо розглянути виробничу функцію при сталих затратах праці, то отримаємо залежності:
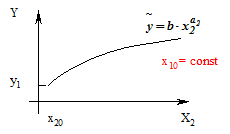
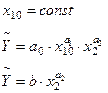
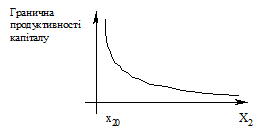
Зобразимо графік граничної продуктивності праці при сталих затратах капіталу, яка задається формулою:
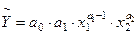
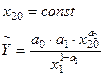 .
.
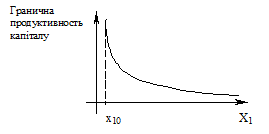
Будуємо графік граничної продуктивності капіталу при сталих затратах праці:
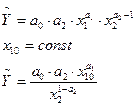
Читайте також:
- Багатомірна лінійна модель регресії.
- Загальна лінійна оптимізаційна модель Канторовича
- Засобами композиції є лінії, штриховка (штрих), тонові й кольорові плями, світлотінь, лінійна і повітряна перспективи [5].
- Лінійна витрата палива
- Лінійна і квадратична локальні інтерполяції
- Лінійна і об’ємна швидкості руху крові у різних ділянках судинного русла. Фактори, що впливають на їх величину.
- Лінійна модель міжнародної торгівлі
- Лінійна модель торгівлі.
- Лінійна модель трансферу технологій
- Лінійна організаційна структура
- Лінійна регресія за допомогою функцій, лінійного тренду та пакета аналізу
- Лінійна рекурентна послідовність, що генерується РЗЛЗЗ
| <== попередня сторінка | | | наступна сторінка ==> |
| Перевірка моделі ПНЛР на адекватність статистичним даним. | | | ТЕМА 6. Мультиколінеарність як особливий випадок моделей множинної лінійної регресії |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |