
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Перевірка моделі ПНЛР на адекватність статистичним даним.
Для оцінки адекватності моделі нелінійної парної регресії експериментальним даним використовуємо критерії Фішера. Розрахункове значення критерію Фішера знаходимо за формулою:
| |
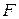 роз =
роз = 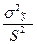 (25),
(25),
де 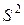 - незсувна і обгрунтована оцінка дисперсії, яка розраховується за формулою:
- незсувна і обгрунтована оцінка дисперсії, яка розраховується за формулою:
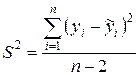 (26),
(26),
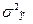 - дисперсія розрахункових значень показника, яка розраховується за формулою:
- дисперсія розрахункових значень показника, яка розраховується за формулою:

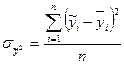 (27).
(27).
Для заданої ймовірності p і числа ступенів вільності k1 = m; k2 = n - m, де n – кількість результатів експерименту; m – кількість факторів, які суттєво впливають на показник, знаходимо табличне значення критерію Фішера Fтабл.
Якщо Fроз > Fтабл, то з ймовірністю p можна стверджувати, що побудувана модель нелінійної парної регресії адекватна експериментальним даним і придатна для економічного аналізу і прогнозування.
У протилежному випадку отриману модель із ймовірністю p не можна вважати адекватною експериментальним даним і не можна використовувати для економічного аналізу і прогнозування.
Зауваження: У розрахункові формули замість значень 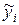 підставляємо значення отримані при підстановці значень
підставляємо значення отримані при підстановці значень 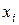 у вихідну формулу нелінійної парної регресії.
у вихідну формулу нелінійної парної регресії.
9.2. Побудова довірчих інтервалів параметрів моделі ПНЛР і теоретичних значень показника. Якщо задана модель парної нелінійної регресії лінійна за фактором 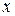 , то довірчі інтервали параметрів шукаємо за тими самими формулами, що і для парної лінійної регресії, а саме:
, то довірчі інтервали параметрів шукаємо за тими самими формулами, що і для парної лінійної регресії, а саме:
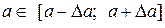 , де
, де
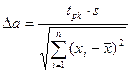 (28),
(28),
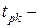 табл. значення функції Стьюдента для ймовірності р і числа ступенів вільності k=n-2.
табл. значення функції Стьюдента для ймовірності р і числа ступенів вільності k=n-2.
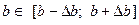 , де
, де
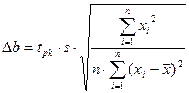 (29).
(29).
Якщо задана модель нелінійна за фактором, причому при зведені її до парної лінійної регресії використали заміну z=j(x), де j(x) – функція нелінійна за фактором х, то для знаходження довірчих інтервалів викорисовують такі формули:
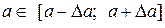 ,де
,де
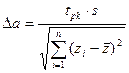 (30),
(30),
 , де
, де
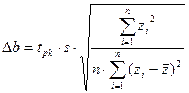 (31).
(31).
Розглянемо порядок побудови довірчої зони регресії. Якщо задана модель парної нелінійної регресії лінійна за фактором 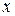 , то відхилення розрахункових значень показника шукаємо за тими самими формулами, що і для парної лінійної регресії, а саме:
, то відхилення розрахункових значень показника шукаємо за тими самими формулами, що і для парної лінійної регресії, а саме:
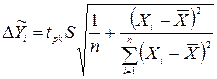 (32).
(32).
У випадку квазілінійної регресії відхилення розрахункових значень показника будуть обчислюватися за формулами:
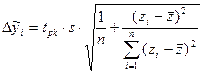 (33).
(33).
Тоді нижня межа парної нелінійної регресії знаходиться за формулами 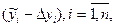 а верхня -
а верхня - 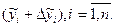
У випадках, коли нелінійна регресія перетворюється у лінійну шляхом логарифмування і заміни величин, довірча зона знаходиться спочатку для лінійної регресії за вищенаведеними формулами, потім, використовуючи зворотні перетворення для меж довірчих інтервалів, знаходимо межі довірчих інтервалів парної нелінійної регресії за формулами:
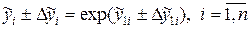 (34).
(34).
Зауваження: Внаслідок використання зворотніх перетворень довірчі інтервали парної нелінійної регресії такого виду будуть несиметричними відносно лінії регресії.
9.3. Прогноз показника та його довірчий інтервал.Для парної нелінійної регресії прогнозне значення показника знаходимо шляхом підстановки прогнозного значення фактора Xp у вихідну формулу.
Якщо задана модель парної нелінійної регресії лінійна за фактором 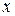 , то відхилення розрахункових значень прогнозу показника шукаємо за тими самими формулами, що і для парної лінійної регресії, а саме:
, то відхилення розрахункових значень прогнозу показника шукаємо за тими самими формулами, що і для парної лінійної регресії, а саме:
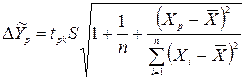 (35).
(35).
Для квазілінійної регресії довірчий інтервал прогнозного значення показника знаходимо за фомулами:
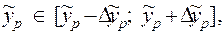 де
де 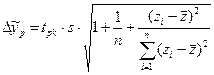 (36).
(36).
| |
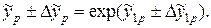 (37).
(37).
9.4. Коефіцієнт еластичності.Загальна формула коефіцієнта еластичності для парної нелінійної регресії має вигляд:
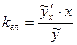 (38).
(38).
Виведемо формули коефіцієнта еластичності для кожного прикладу:
1) 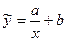 ,
,
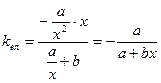 .
.
2) 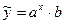 ,
,
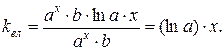
3) 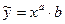 ,
,
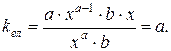
4) 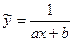 ,
,
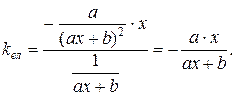
5) 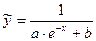 ,
,
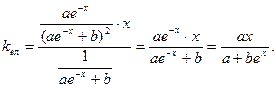
6) 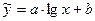 ,
,
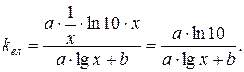
7) 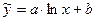 ,
,
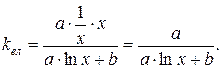
8) 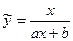 ,
,
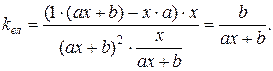
9)  ,
,
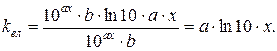
| |
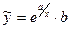 ,
,
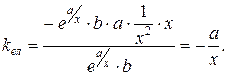
11) 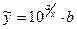 ,
,
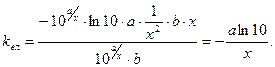
12) 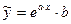 ,
,
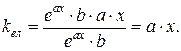
13) 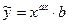 ,
,
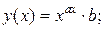

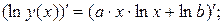

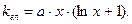
14) 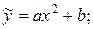
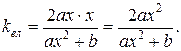
15) 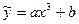 ,
,
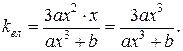
| |
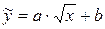 ,
,
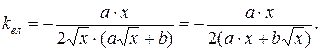
10. Приклади застосування моделей ПНЛР у бізнесі та фінансах. Приклад 1. Для прогнозування попиту на товари тривалого користування використовують логістичну регресію 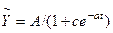 , де -
, де - 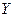 забезпеченість товаром, t – час,
забезпеченість товаром, t – час,  - насиченість ринку товаром. Попит на товари тривалого користування має таку тенденцію до зміни: спочатку деякий час попит зростає, а потім коливається навколо сталого числа.
- насиченість ринку товаром. Попит на товари тривалого користування має таку тенденцію до зміни: спочатку деякий час попит зростає, а потім коливається навколо сталого числа.
Приклад 2. Для аналізу залежності між витратами на споживання та доходом використовують криву Енгеля, яка задається формулою :
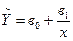 , де
, де
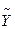 - витрати на споживання,
- витрати на споживання,
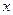 - дохід,
- дохід, 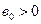 ,
, 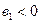
Графік даної залежності має такий вигляд :
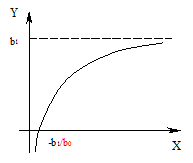
Критична точка 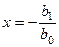 визначає рівень доходу, нижче якого товар не буде куплений. Якщо дохід збільшується, то і збільшуються витрати на споживання, але до певної межі
визначає рівень доходу, нижче якого товар не буде куплений. Якщо дохід збільшується, то і збільшуються витрати на споживання, але до певної межі 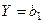 , яка називається “межею насичення”, тобто, якщо ми задовільнили потребу у певних товарах, то, незважаючи на збільшення доходу, цей товар купуватися небуде.
, яка називається “межею насичення”, тобто, якщо ми задовільнили потребу у певних товарах, то, незважаючи на збільшення доходу, цей товар купуватися небуде.
Читайте також:
- CMM. Визначення моделі зрілості.
- II. Перевірка домашнього завдання.
- II. Перевірка домашнього завдання.
- II. Перевірка домашнього завдання.
- II. Перевірка домашнього завдання.
- II. Перевірка домашнього завдання.
- II. Перевірка домашнього завдання.
- II. Перевірка домашнього завдання.
- II. Перевірка домашнього завдання.
- II. Перевірка домашнього завдання.
- ISO 15504.Структура еталонної моделі
- IV. Перевірка розв’язання і відповідь
| <== попередня сторінка | | | наступна сторінка ==> |
| | | ТЕМА 5. Множинна лінійна регресія |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |