• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Наслідки порушення припущення про гомоскедастичності.

1.У випадку гетероскедастичності не можна використовувати формули для знаходження дисперсії параметрів.

2. У випадку гетероскедастичності збільшення дисперсії параметрів призводить до збільшення довірчих інтервалів параметрів іпоказника, та до того, що розрахункові значення та критерії будуть меншими за табличні, тобто неможливо провести аналіз моделі.

3. Тестування наявності гетероскедастичності. Для виявлення гетероскедастичності викорстовують такі методи:

1. Аналіз змісту проблеми. Часто явище гетероскедастичності можна виявити інтуїтивно, проаналізувавши зміст даної задачі.

2. Графічний аналіз. Для використання цього методу потрібно знайти квадрати відхилень розрахункових значень показника від теоретичних та проаналізувати їх залежність від показника У. За цією залежністю можна визначити наявність або відсутність гетероскедастичності у даній задачі.

3. Тест рангової кореляції Спірмана. Розглянемо алгоритм даного методу:

1. Будємо рівняння регресії і знаходимо l_i.

2. Розглядаємо абсолютні значення відхилень l_i і будуємо рангований ряд величин у зростаючому або спадаючому порядку. Розраховуємо коєфіцієнт рангової кореляції Спірмана за формулою:

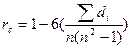(4),

де 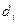- різниця між рангом відхилень ,

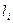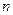- кількість значень .

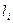3. Перевіряємо значимість коефіцієнта Спірмана за критерієм Стьюдента:

(5).

За величиною ймовірності р і числом ступенів вільності 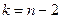знаходимо табличне значення критерію Стьюдента і перевіряємо умову:

.

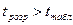Якщо вона виконується, то з ймовірністю р робимо висновок про наявність гетероскедастичності, в протилежному випадку – гетероскедастичність відсутня.

4. Тест Голдфелда Квондта. Він використовується для великої кількості спостережень (більше 30).

Алгоритм методу:

1) будуємо ранговий ряд в порядку зростання або спадання за одном із незалежних факторів;

2) вибираємо кількість центрованих значень с=8, тобто

с=8 для n=30,

с=8 для n=60.

Розглядаємо дві підвибірки, які утворюються шляхом виключення центровочних значень.

Для кожної з цих підвибірок будуємо регресію і знаходимо відхилення:

, .

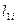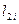
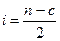Знаходимо розрахункове значення F-критерію за формулою:

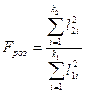(6).

Табличне значення критерію знаходимо за величиною ймовірності р та кількістю ступенів вільності 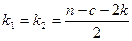, де 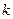- загальна кількість параметрів.

Перевіряємо умову 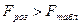. Якщо вона виконується, то для даної моделі властиве явище гетероскедастичності, в іншому випадку гетероскедастичність відсутня.

4. Оцінка параметрів узагальненим методом найменших квадратів у випадку гетероскедастичності.Оскільки наявність гетероскедастичності є порушенням одного з класичних припущень моделі МЛР, то використовувати МНК для знаходженні параметрів не можна. У цьому випадку використовувати узагальнений метод найменших квадратів УМНК або метод Ейткена.

Розглянемо застосування даного методу на частковому випадку множинної лінійної моделі – ПЛР. Запишемо ПЛР у такому випадку:

(7).

Припустимо, що для моделі властиве явище гетероскедастичності і відомі всі значення .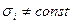

Перепишемо (7) у такому вигляді:

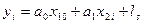(8),

де =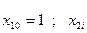

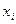
Поділимо обидві частини даного рівняння на величину 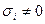, отримаємо:

,

(9).

Покажемо, що для даної моделі відсутнє явище гетероскедастичності, тобто :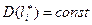

.

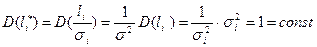Отже, перетворення, які ми застосували дозволяють позбутись явища гетероскедастичності і до перетвореної молелі (9) можна застосувати МНК.

Даний підхід називається методом УМНК

Розглянемо принцип перетворення моделі за методом УМНК. Часто у випадку гетероскедантичності задається залежність між дисперсією відхилень 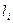та значеннями 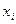, наприклад, .

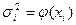Розглянемо приклад:

1. .

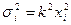
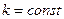Розглянемо на прикладі ПЛР:

.

Поділимо обидві частини данного рівняння на величину :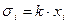

.

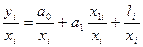Покажемо, що у цьому випадку відсутнє явище гетероскедантичності, тобто виконується умова:

,

.

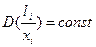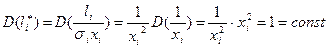2. ,

, ,

, ,

.

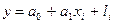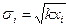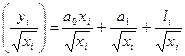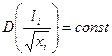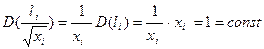3. ,

, ,

,

,

.

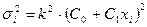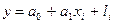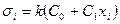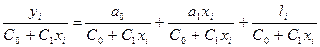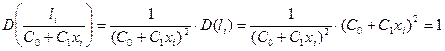Отже, зробимо таке узагальнення: якщо для моделі властиве явище гетероскедантичності і відома залежність 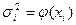, то розділивши цю модель на вираз 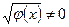, отримаємо модель, до якої можна застосовувати звичайний метод найменших квадратів.

Читайте також:

1. F) Наслідки демографічного вибуху.
2. Аварії, що супроводжуються пожежами. Наслідки пожеж.
3. Адміністративна відповідальність за порушення аграрного законодавства
4. Адміністративна відповідальність за порушення земельного законодавства
5. Адміністративна відповідальність за порушення митних правил
6. Адміністративна відповідальність за порушення податкового законодавства.
7. Адміністративне правопорушення
8. Адміністративне правопорушення як підстава юридичної відповідальності: ознаки і елементи
9. Адміністративне правопорушення як підстава юридичної відповідальності: ознаки і елементи.
10. Адміністративне правопорушення, його ознаки та склад
11. Адміністративне правопорушення.
12. Адміністративний арешт активів та його наслідки

Переглядів: 819