• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

ТЕМА 8. Автокореляція в економетричних моделях динаміки

План

1. Поняття автокореляції.

2. Тестування автокореляції.

3. Поняття дистрибутивно-лагових та авторегресивних моделей.

4. Оцінка параметрів дистрибутивно-лагових моделей.

4.1. Метод послідовної оцінки параметрів.

4.2. Підхід Койка до дистрибутивно-лагових моделей.

5. Модифікація моделей Койла.

5.1. Модель адаптивних очікувань: перша модифікація моделі Койка.

5.2.Модель часткових пристосувань: друга модифікація моделей Койка.

6. Оцінка параметрів моделі Койка та її модифікацій методом допоміжної змінної .

7. Підхід Альмона до дистрибутивно-лагових моделей.

1. Поняття автокореляції.Одним із припущень класичної моделі МЛР є припущення про незалежність випадкових величин 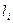та 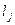. Випадок порушення цього припущення називається автокореляцією (порушення четвертого припущення), тобто 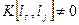при .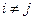

Автокореляцією називають залежність між значеннями довільної вибірки із запізненням в один часовий період (лаг).

Автокореляцію називають серійною, якщо така залежність існує між значеннями різних вибірок:

.

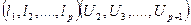Автокореляція може виникати у зв‘язку з інерційністю та циклічністю багатьох економічних процесів. Це є негативним явищем МРА (множинного регресійного аналізу), оскільки в цьому випадку не можна застосовувати МНК для знаходження параметрів моделі.

Крім того, у цьому випадку значення F та t-статистик, будують меншими за табличні, тобто провести аналіз моделі буде неможливо.

2. Тестування автокореляції. Для виявлення автокореляції застосовуємо тест Дарбіна-Уотсона. Розглянемо коротко алгоритм цього тесту.

1. Знаходимо розрахункове значення тесту за формулою:

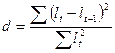(1).

Теоретично доведено, що розрахункове значення d-критерію знаходиться в межах .

2. За ймовірністю р, кількість результатів досліджень n та кількістю факторів моделі k знаходимо 2 табличні значення та .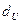

3. Залежності від того, де буде знаходитись розрахункове значення щодо 2 табличних, робимо висновок про наявність або відсутність автокореляції. Зокрема, якщо 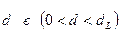, то це свідчить про наявність позитивної автокореляції. Якщо значення 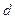потрапляє в зону невизначеності, тобто набуває значення 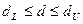, або 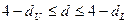, то ми не можемо зробити висновки ні про наявність, ні про відсутність автокореляції. Якщо 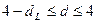, то маємо негативну автокореляцію. Нарешті, якщо , то автокореляції немає.

Якщо значення 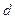потрапляє в зону невизначеності, то робимо висновок, що в даних умовах неможливо визначити, наявна чи відсутня автокореляція. Для цього використовують додатковий тест, який називається h-тест.

3. Поняття дистрибутивно-лагових та авторегресивних моделей.Регресійна модель, яка включає в себе не лише поточні, а й попередні значення незалежних змінних, називається дистрибутивно-лаговою моделлю.

Регресійна модель, яка включає в себе одну або більше попередніх значень залежної змінною називається авторегресивною моделлю.

Розглянемо приклади дистрибутивно-лагових та авторегресивних моделей.

Дистрибутивно-лагова модель зі скінченим лагом в 2 періоди:

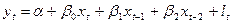(2).

Дистрибутивно-лагова модель зі скінченим лагом в k періодів:

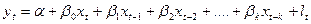(3).

Нескінченно дистрибутивно-лагова модель:

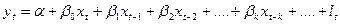(4).

Авторегресивна модель:

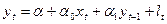(5).

Розглянемо детальніше дистрибутивно-лагову модель (3). Параметр 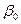цієї моделі називається короткостроковим мультиплікатором і показує вплив змінної х на зміну значення y в поточний період часу.

Якщо зміна значення х триває, то 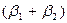показує зміну показника у другий період, 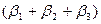- в третій і так далі. Ці часткові суми називаються проміжними мультиплікаторами.

Через k періодів отримаємо 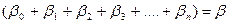, що називається сумарним або довгостроковим мультиплікатором і характеризує сумарний вплив зміни фактора х у різні періоди часу. Прикладом дистрибутивно-лагової моделі може бути функція споживання.

Наприклад :

,

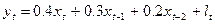де 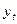- витрати на споживання,

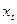- дохід.

Ця функція має зміст, оскільки відомо, що при збільшенні доходу витрати на споживання збільшуються поступово.

4. Оцінка параметрів дистрибутивно-лагових моделей. 4.1. Метод послідовної оцінки параметрів.Даний метод грунтується на припущенні послідовного оцінювання, а саме:

- спочатку будується залежність між ,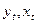

- потім ,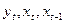

-

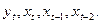
Процедура побудови припиняється тоді, коли параметри при незалежних змінних (х) стають статистично незначимими і в наступному рівнянні змінюють свій знак на протилежний.

Зауваження. Метод має недоліки:

- наперед невідома величина лагу;

- метод не враховує явища мультиплікаторності.

Читайте також:

1. S Визначення оптимального темпу роботи з урахуванням динаміки наростання втоми.
2. VІII. Основи молекулярної фізики і термодинаміки
3. Автокореляція
4. Автокореляція залишків – це залежність між послідовними значеннями стохастичної складової моделі.
5. Аналіз вимог та динаміки попиту на міжнародному та внутрішньому ринку туристичних послуг (за видами туризму, за категоріями туристів, цілей та об’єктів відвідування)
6. Аналіз динаміки витрат і крива досвіду
7. Аналіз динаміки і структури валового нагромадження.
8. Аналіз динаміки і структури витрат підприємства
9. Аналіз динаміки ринку, модель життєвого циклу
10. Аналіз динаміки розвитку фабрик програм
11. Аналіз динаміки та структури банківських доходів
12. Аналіз динаміки та структури валютних операцій

Переглядів: 1240