• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Підхід Койка до дистрибутивно-лагових моделей.

Цей метод грунтується на припущені, що параметри 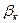перебувають між собою в залежності, мають один і той самий знак і змінюються за законом геометричної прогресієї, тобто:

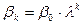(6).

Величина 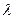називається темпом зменшення дистробутивного лагу. Ця формула є досить логічною, тому що з плином часу вплив фактора на показник стає все меншим.

Враховуючи припущення (6) довгостроковий мультиплікатор , який дорівнює сумі всіх параметрів буде обчислюватися за формулою:

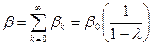(7).

Цей ряд є збіжний і має скінчену суму.

Розглянемо нескінченну дистрибутивно-лагову модель (4) і застосуємо до неї припущення Койка (6):

,

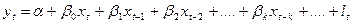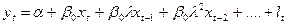(8).

Припустимо, що модель (8) справедлива і в попередній момент часу t-1

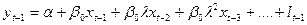(9).

Помножимо рівняння (9) на :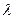

Позначимо перетворене рівняння через (10). Віднімемо рівняння (8) і (10) і отримаємо:

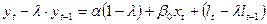(11).

(11) – модель Койка. Перепишемо модель Койка у вигляді:

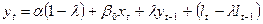(12).

Рівняння (12) має набагато простіший вигляд порівняно з початковою моделлю (4), однак вона має і ряд недоліків:

- перетворення Койка переводять дистрибутивно-лагову модель у клас авторегресивних моделей;

- не розглядається питання можливості мультиколінеарності 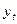та ;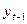

-для перевірки автокореляції не можна використовувати тест Дарбіна-Уотсона.

Читайте також:

1. III етап. Системний підхід
2. IV етап. Ситуаційний підхід
3. Аксіологічний підхід до вивчення педагогічних явищ.
4. Аксіоми безпеки життєдіяльності. Системний підхід в БЖД
5. Алфавітний підхід до вимірювання кількості інформації.
6. Асимптотичний підхід до порівняння оцінок
7. Багатоаспектний підхід до прийняття управлінськихрішень
8. Багаторівневий підхід. Протокол. Інтерфейс. Стек протоколів.
9. Вибір моделей.
10. Витратний підхід
11. Віковий підхід і взаємодія різних рівнів соціального досвіду в діяльності різновікових дитячих об’єднань. Функції різновікової групи.
12. Гібридний підхід

Переглядів: 790