Новини освіти і науки:

G+

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Модифікація моделей Койла. 5.1. Модель адаптивних очікувань: перша модифікація моделі Койка.

Розглянемопобудову моделі адаптивних очікувань на прикладі:

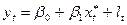(13),

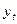- попит на гроші,

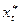- очікувана довгострокова або звичайна відсоткова ставка,

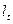- відхилення.

Оскільки величина 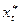не може бути визначена на даному етапі (це майбутнє значення) в економіці запропонована гіпотеза помилкового навчання або адаптивного очікування, яка має вигляд:

(14).

Суть гіпотези полягає в тому, що майбутнє значення з деяким множником залежить від теперішнього значення. В майбутньому ми використовуємо теперішній досвід з деяким відхиленням, тобто пристосовуючи його до конкретної ситуації, або, інакше, вчимося на помилках.

Визначимо з даної гіпотези 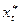і підставимо у рівняння (13):

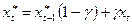(14),

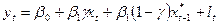(15).

Припустимо, що модель (13) справедлива в попередній період часу t-1:

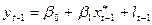(16).

Домножимо (16) на :

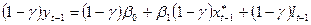(17).

Віднімаємо (15) і (17):

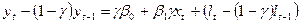(18).

Після спрощення отримаємо:

(19).

(19) – перша модифікація моделі Койка (модель адаптованих очікувань). Вона має набагато простіший вигляд порівняно з початковою моделлю, однак недоліком є складний вигляд відхилення .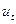

5.2.Модель часткових пристосувань: друга модифікація моделі Койка.Розглянемо побудову моделі часткових пристосувань на прикладі:

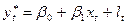(20),

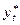- бажаний рівень капіталу,

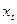- випуск продукції,

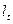- випадкова величина.

Оскільки бажаний рівень капіталу 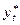не можна оцінити безпосередньо, то використовується гіпотеза, яка називається гіпотезою часткових пристосувань:

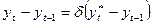(21),

де 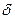- коефіцієнт пристосування

Коротка суть гіпотези полягає в наступному: фактична зміна капіталу (інвестиції) є деякою часткою від бажаної зміни за цей період.

Підставимо значення 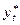з формули (20) у формулу (21), попередньо перетворивши її:

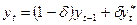(22).

Після перетворення, отримаємо:

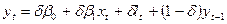
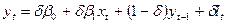(22).

(22) – друга модифікація моделей Койка, яка називається модель часткових пристосувань.

Їй властиві усі недоліки загальної моделі Койка.

6. Оцінка параметрів моделі Койка та її модифікацій методом допоміжної змінної .Неможливість застосування МНК до моделі Койка та її модифікацій виявляється в тому, що змінна величина 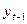може корелювати з відхиленням 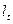, тому для оцінки параметрів моделей Койка використовують метод допоміжної змінної.

Суть методу допоміжної змінної полягає в тому, що вводять деяку допоміжну змінну 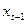, для змінної 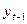, припускаючи, що допоміжна змінна корелює з 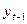, і не корелює з відхиленням 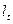. У загальному випадку усі розглянуті авторегресивні моделі (модель Койка, модель адаптивних очікувань і часткових пристосувань) можна записати у такому вигляді:

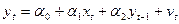(23).

Для оцінки параметрів рівняння (23) використовуємо метод допоміжної змінної. Система нормальних рівнянь для рівняння (23) буде мати такий вигляд:

(24)

Розв‘язавши систему (24) методом ЗЖВ, отримаємо параметри 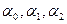моделі (23).

Зауваження.Хоча метод допоміжної змінної простий у застосуванні, він не є універсальним тому що змінні 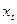, та 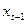можуть бути колінеарні між собою. Такий випадок зменшує сферу застосування методу.

7. Підхід Альмона до дистрибутивно-лагових моделей.Усі розглянуті вище динамічні моделі грунтуються на припущенні про те, що параметри цих моделей спадають у геометричній прогресії. Це є часткове припущення, яке обмежує клас розглянутих задач. У загальному випадку параметри 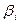можна виразити як функцію від числа t з наперед заданою тривалістю часовою лагу.

Саме такий підхід запропонував Альмон для знаходження параметрів дистрибутивно-лагових моделей. Розглянемо застосування даного підходу на прикладі дистрибутивно-лагової моделі скінченного лагу k:

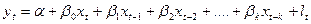(3).

Альмон використовував теорему Веєрштрасса з математичного аналізу про те, що параметр 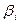можна апроксимувати (представити) многочленом відповідного ступеня від числа і з наперед заданою тривалістю часового лагу.

На практиці було показано, що найточніші результати отримуються при використанні многочленів 2 і 3 ступеня:

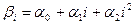Зауваження.В загальному випадку для представлення параметра 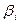можна застосовувати многочлен будь-якого ступеня. При цьому отримані результати будуть достовірними, однак найбільша точність досягається при використанні многочленів 2 і 3 ступеня. Застосуємо многочлен 2-го степення до рівняння (3), записавши його в скороченому вигляді:

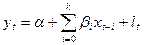(25).

Отримаємо:

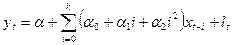(26).

Спростивши вираз (26), отримаємо:

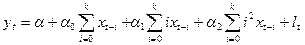(27).

Введемо заміну змінних:

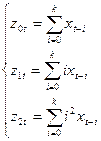(28).

Після заміни отримаємо рівняння 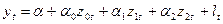(29):

(29).

(29) – рівняння лінійної множинної регресії, до якого можна застосувати метод найменших квадратів (класичний).

Підхід Альмона є найкращим серед всіх розглянутих методів, однак має такі недоліки:

1) максимальна тривалість часового лагу повинна бути визначена самостійно відповідно до кількості даних показників;

2) потрібно самостійно визначити ступінь многочлена, яким задається параметр .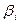

Рекомендується вибирати многочлен 2-го ступеня.

Розв‘язавши рівняння (29) методом МНК, ми знайдемо параметри 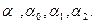Для знаходження параметрів 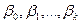використовують представлення параметра 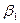многочленом 2-го степення:

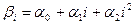
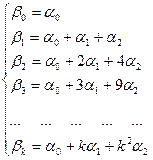(30).

(30) задає значення параметрів дистрибутивно-лагової моделі (3).

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
Підхід Койка до дистрибутивно-лагових моделей.	\|	ТЕМА 9. Методи дослідження якісних економічних показників

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.005 сек.