Новини освіти і науки:

G+

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Практичне заняття 5.

Тема заняття.Застосування похідної до розв’язування рівнянь та нерівностей.

1. Застосування похідної до розв’язування рівнянь.

2. Застосування похідної до розв’язування нерівностей.

1. Застосування похідної до розв’язування рівнянь.

Теоретичний матеріал. З курсу алгебри і початків аналізу вам відомо, що під час розв’язування деяких рівнянь ефективно використовувати властивості функцій, а саме скінченність ОДЗ, обмеженість множини значень, зростання та спадання.

Іноді для з’ясування потрібних властивостей функцій доцільно використовувати похідну. Це перш за все дослідження проміжків зростання і спрадання функції та оцінка області значень функції.

Відповідні прийоми такого дослідження представлені у підручнику [18].

Згадаємо їх.

1) Оцінка лівої та правої частин рівняння.

Якщо потрібно розв’язати рівняння виду 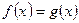і з’ясувалось, що 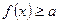, , 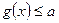то рівність між лівою і правою частинами рівняння можлива лише у випадку, якщо одночасно і 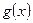дорівнюють .

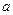Тобто 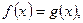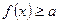, , 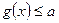тоді і тільки тоді коли .

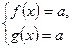2) Під час розв’язування рівнянь використовують зростання і спадання функцій.

На основі наступних властивостей обґрунтовується єдність кореня рівняння, який знаходять підбором.

Властивість 1. Якщо функція 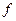зростає або спадає на деякому проміжку, то на цьому проміжку рівняння 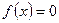має не більше одного кореня.

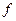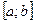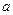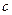Властивість 2. Якщо функція визначена і неперервна на проміжку і на його кінцях приймає значення різних знаків, то між і знайдеться точка в якій .

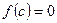Властивість 3. Якщо в рівнянні 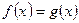функція зростає на деякому проміжку, а функція 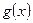спадає на цьому ж самому проміжку (або навпаки), то це рівняння може мати не більше ніж один корінь на цьому проміжку.

Якщо ми змогли підібрати два корені заданого рівняння виду 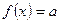, то щоб довести, що рівняння не має інших коренів, достатньо впевнитися, що функція має тільки два проміжки зростання чи спадання.

Для того щоб диференційована на інтервалі функція мала на цьому інтервалі не більше двох проміжків зростання чи спадання, достатньо щоб на цьому інтервалі вона мала тільки одну критичну точку.

Розглянемо приклади розв’язування рівнянь методом оцінки.

Приклад 1.Розв’яжіть рівняння:

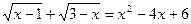Розв’язання. Нехай , .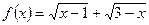

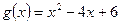Оцінимо їх значення.

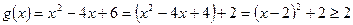Для оцінки множини значень функції використаємо похідну.

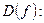
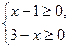
Отже, .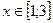

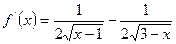. Похідна не існує в точках 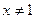і 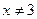. Ці точки не є внутрішніми точками 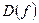, і отже, не є критичними.

Знайдемо критичні точки:

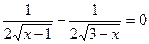. Розв’язавши рівняння, одержуємо 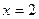. Це єдина критична точка на відрізку .

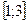Оскільки функція неперервна на відрізку 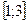і має на ньому скінченне число критичних точок, то вона набуває найбільшого та найменшого значень або на кінцях відрізка або в критичній точці.

Обчисливши 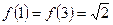, , 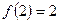з’ясовуємо, що 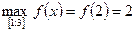, тобто .

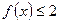Отже рівняння рівносильне системі рівнянь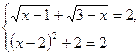

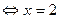
Відповідь. 2.

Приклад 2.Розв’яжіть рівняння

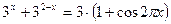Розв’язання. ОДЗ рівняння .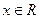

Нехай , .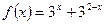

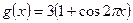Оцінимо їх значення:

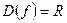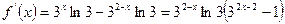. похідна існує на всій 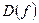. Прирівнявши її до нуля знаходимо, що 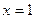- єдина критична точка. З’ясувавши, що при переході через цю точку похідна змінює знак з ”-” на ”+”, робимо висновок, що це точка мінімуму. Оскільки вона єдина на всій області визначення, то в ній функція досягає свого найменшого значення.

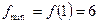. Отже, .

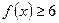Оцінимо функцію .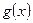

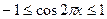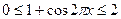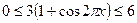Отже, .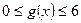

Тому рівняння рівносильне системі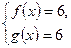

Але значення 6 функція набуває тільки при 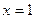, що задовольняє і друге рівняння системи .

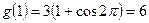Отже, одержана система (а значить і задане рівняння) має єдиний розв’язок .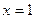

Відповідь. 1.

Розглянемо, як використовується зростання і спадання функцій при розв’язуванні рівнянь.

Приклад 3.Розв’яжіть рівняння .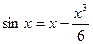

Розв’язання. Легко бачити, що 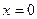є коренем рівняння. Покажемо, що інших коренів це рівняння не має. Дослідимо функцію 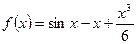на монотонність.

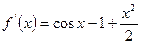. Встановимо проміжки, на яких функція 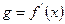зберігає знак. Для цього дослідимо її на монотонність .

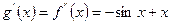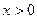
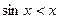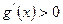Оскільки при , то при 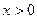. Отже, функція 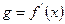зростає при додатних значеннях 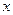. . 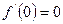Тому при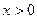 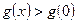, тобто .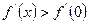

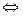
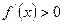На основі парності функція 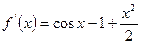набуває додатних значень при всіх 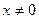. Отже, зростає на всій числовій осі. Згідно з властивістю 1, рівняння 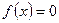має не більше одного кореня.

Отже, 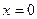- єдиний корінь рівняння.

Відповідь. 0.

Приклад 4.Розв’яжіть рівняння .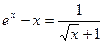

Розв’язання. Легко визначити, що 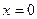є коренем рівняння.

Покажемо, що інших коренів рівняння не має.

ОДЗ .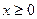

Розглянемо функції , .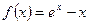

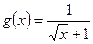Дослідимо їх на монотонність.

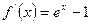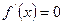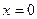. при . Але 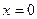не є критичною точкою.

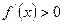при .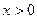

Враховуючи неперервність функції , одержуємо, що зростає при .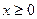

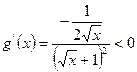при 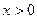. Отже, 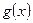спадає при .

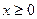За властивістю 3 рівняння має єдиний корінь .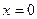

Відповідь. 0.

Розглянемо приклад рівняння яке має два корені та розв’язується на основі властивостей функцій.

Приклад 5.Розв’яжіть рівняння .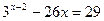

Розв’язання. Легко впевнитись, що задане рівняння має два корен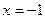і і .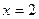

Доведемо, що інших коренів це рівняння не має. Для цього достатньо довести, що функція 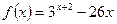має не більше двох проміжків зростання чи спадання.

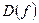
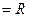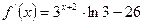- існує на всій області визначення функції.

Знайдемо критичну точку, розв’язавши рівняння 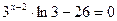. Виявляється що, 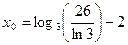- єдина критична точка функції.

На проміжку 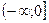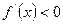, отже, функція спадає, а на проміжку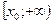 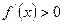, отже, функція зростає.

Тоді на кожному з проміжків, за властивістю 1, рівняння 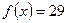може мати не більше ніж один корінь, тобто всього задане рівняння може мати не більше ніж два корені.

Відповідь. -1; 2.

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
ЗАВДАННЯ ДЛЯ САМОСТІЙНОЇ РОБОТИ	\|	ЗАВДАННЯ ДЛЯ САМОСТІЙНОЇ РОБОТИ 1

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.005 сек.