Координати в геодезії

Положення точки на фізичній поверхні Землі визначається системою координат – лінійними та кутовими величинами. В геодезії використовують різні системи координат. Складаючи карти великих територій земної поверхні та працюючи на них, користуються географічними координатами. Місцезнаходження точки у цій системі визначають її довгота й широта. Довготою точки називають кут між площинами початкового (нульового) меридіана й меридіана, проведеного через цю точку. За початковий прийнято вважати Гринвіцький меридіан, який проходить через м. Гринвіч поблизу Лондона. Розрізняють східну й західну довготи. Їхні значення змінюються від 0 до 180°. Широта точки – кут між перпендикуляром, опущеним з неї до центру Землі й площиною екватора. Широти змінюються від 0 до 90° і можуть бути північними або південними, залежно від того, у якій півкулі знаходиться точка. Географічні координати точок земної поверхні визначають за даними астрономічних спостережень.

Для виготовлення топографічних карт (планів) і обчислення координат пунктів опорних геодезичних мереж застосовують поперечно-циліндричну рівнокутну проекцію Гаусса. Земну поверхню ділять через 6° меридіанами на 60 зон, кожну з яких проектують на бічну поверхню циліндра, котру після цього розгортають у площину (рис. 13). Зручні робочі формули для обчислень координат точок у цій системі запропонував Крюгер, тому вона носить назву зональної системи прямокутних координат Гаусса-Крюгера.

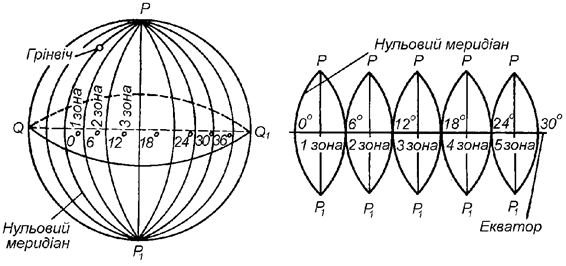
Рис. 13. Зональна система координат Гаусса-Крюгера

Координати точок у кожній зоні визначають за їхніми відстанями від екватора X та від осьового меридіана зони Y. Оскільки територія нашої країни розташована на північ від екватора, то значення абсцис точок на її поверхні завжди будуть додатними. Щоб уникнути від’ємних значень ординат, значення Y початку координат беруть +500 км. Попереду ординати вказують номер зони, в якій знаходиться дана точка. Наприклад, якщо точка А у зоні 6 віддалена на захід від осьового меридіана на відстань 45235 м, то значення її абсциси дорівнюватиме Y_А = 500000 – 45235 = 454765 м, а з урахуванням номера зони Y_А= 6454765 м

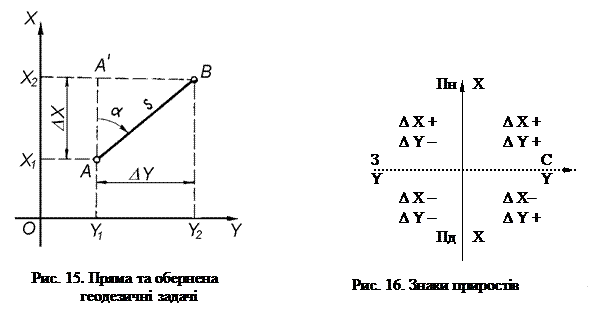
Складаючи плани невеликих ділянок землі, найчастіше користуються місцевою системою прямокутних координат, початком якої може бути будь-яка точка земної поверхні, а положення точки на площині визначають шляхом її проектування на вісь ординат і вісь абсцис (рис. 14). Слід пам’ятати, що в геодезії (на відміну від аналітичної геометрії) вісь абсцис ("іксів") суміщена з напрямом меридіана, а вісь ординат ("ігреків") – перпендикулярна до неї. Положення точки, наприклад А, визначається відстанями від початку координат до основ перпендикулярів, опущених із неї на осі абсцис і ординат. Ці відстані і є координатами X та Y даної точки.

Проводячи геодезичні зйомки, часто користуються полярними координатами. За їхній початок (полюс) беруть точку, координати якої відомі (геодезичний пункт, перехрестя доріг чи лісових просік, тахеометричну станцію тощо), а за початковий напрям – напрям на іншу точку з відомими координатами. Положення точки на місцевості визначають за кутом між початковим напрямом і напрямом на дану точку та відстанню до неї. Кути відлічують за годинниковою стрілкою. Полярна система координат слугує основою для топографічних зйомок місцевості (тахеометричної, мензульної) .

З перерахованих систем координат тільки географічна може бути поширена на всю територію земної поверхні. Однак, її використання в інженерній геодезії обмежене тим, що координати точок тут визначають у градусній мірі, в той час як відстані вимірюють у метрах. Зональна система координат дозволяє перетворювати географічні координати точок місцевості у прямокутні. Разом із тим, ці обчислення є досить громіздкими і вимагають значних затрат часу.

Обчислення прямокутних координат точок пов’язані з розв'язуванням прямої та оберненої геодезичних задач. Пряма геодезична задача полягає у визначенні за відомими координатами початку лінії АВ (X_А і Y_А), її румбом R і горизонтальною проекцією S координат кінця цієї лінії – точки В. Обернена задача передбачає визначення за відомими координатами початку та кінця лінії її довжини та напряму (рис. 15). Розв’язуючи ці задачі, необхідно з`ясувати поняття про прирости координат. Ними є довжини катетів прямокутного трикутника 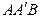– DX та DY. Як видно з рисунка, прирости координат можна обчислити за формулами:

DX = S × cos R;

DY = S × sin R.

Залежно від напряму лінії (назви румбу), прирости координат можуть бути додатними або від'ємними (рис. 16). Координати точки В знаходять за формулами:

X_В = X_А + DX_АВ;

Y_В = Y_А + DY_АВ,

тобто координата наступної точки дорівнює координаті попередньої плюс відповідний приріст координат (із його знаком).

Для розв’язку оберненої геодезичної задачі обчислюють прирости координат лінії AB за формулами:

DX_АВ = X_В - X_А;

DY_АВ= Y_В - Y_А,

а потім знаходять її напрям. За формулою 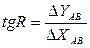обчислюють тангенс румба цієї лінії, а за ним – його кутове значення. Назву румба встановлюють за знаками приростів координат.

Довжина лінії АВ:

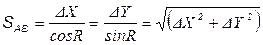Необхідність у розв’язуванні оберненої геодезичної задачі виникає у процесі прив’язки до опорних пунктів, тобто передачі дирекційного кута (азимута) на лінію полігону та координат на одну з його вершин від точок із відомими координатами. Визначивши таким чином румб лінії між пунктами геодезичної мережі, його переводять в азимут, а далі, використовуючи залежність між азимутами і внутрішніми кутами полігону, обчислюють азимути усіх його сторін.

Геодезична мережа складається з точок земної поверхні, положення яких визначено в єдиній системі координат. Якщо відомі лише планові координати X та Y пунктів геодезичної мережі, то така мережа називається плановою, якщо відомі тільки висоти Н пунктів – висотною (нівелірною), коли відомі і планові, і висотні координати – планово-висотною. За своїм призначенням і точністю побудови геодезичні мережі поділяються на державну, мережі згущення та знімальні мережі. Державні геодезичні мережі досягають густоти один пункт на 5…15 км². Подальше згущення відбувається за рахунок мереж згущення та знімальних мереж.

Планове положення пунктів геодезичних мереж визначають методами тріангуляції, трилатерації, полігонометрії. У першому випадку геодезична мережа являє собою систему трикутників, у яких виміряні всі кути та довжини деяких із сторін – базиси. Метод трилатерації полягає у визначенні планових координат пунктів за виміряними довжинами сторін та одним кутом. Використовуючи метод полігонометрії, вимірюють відстані та кути між пунктами.

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
Азимути, румби, дирекційні кути	\|	Поняття про геодезичні зйомки. Складання технічних документів

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.017 сек.