• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Операції над подіями

Сумою двох випадкових подій А і В називають таку подію, яка полягає в появі хоча б однієї з подій А або В, і позначають А + В (або А È В).

Сумою п випадкових подій А₁,А₂,...,А_n називають таку подію, яка полягає в появі принаймні однієї з цих подій (позначається ).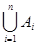

Добутком двох випадкових подій А і В назівають таку подію, яка полягає в сумісній появі обох подій А і В, і позначають А • В (або А Ç В).

Добутком п випадкових подій А₁,А₂,...,А_п називають таку подію, яка полягає в сумісній появі всіх цих подій (позначається ).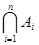

Різницею двох випадкових подій А і В називають таку подію, яка полягає в виконанні події А і не виконанні події В, позначається як А – В, або А \ В.

Подію називають протилежною до події А в даному випробуванні, якщо вона відбувається, якщо не відбувається подія А, тобто = Ω – А. Очевидно, протилежні події не сумісні і утворюють повну групу подій.

Поняття суми і добутку подій можуть бути узагальнені на випадки будь-якого числа подій.

З визначення операцій додавання і множення слідують співвідношення:

1) A + А = A; A ‧ А = A ;

2) A + U = U; A ‧ U = A;

3) A+ Æ = A ; A‧ Æ = Æ;

4) A + B = B + A ; A ‧ B = B ‧ A;

5) (A + B) + C = A + (B + C); (A ‧ B) ‧ C = A‧ (B ‧ C);

6) A ‧ (B + C) = A ‧ B + A ‧ C.

Приклад 1. У ящику містяться кульки білого та чорного кольору. Навмання з нього виймають одну кульку. Подія А = {вийнято куль­ку білого кольору}, подія В = {вийнято кульку чорного кольору}. Сумісні чи несумісні ці події?

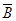Розв’язання. Ці події несумісні, тому що поява події А виключає виконання події В, також події А і В утворюють повну групу події і є протилежні: = В, = А.

Приклад 2. Підкидають два гральних кубики. Нехай події А_і = {випаде і очок та першому кубику}, і = 1, 2, 3,4, 5, 6, B_j = {випа­де і очок та другому кубику}, і = 1, 2, 3,4, 5, 6. Виразити через А_і,і B_j такі події:

а) сума очок на двох кубиках дорівнює п'яти;

б) випаде в сумі хоча б десять очок;

в) випаде в сумі не більше трьох очок.

Розв'язання.

а) Нехай С₁= {сума очок на двох кубиках дорівнює п’яти}. Ця подія можлива тільки тоді, коли на першому кубику випаде і очок, а та другому j очок так, щоб і + j = 5, тобто і =1, j =4, або і = 2, j = 3, або і = 3, j = 2, або і = 4, j = 1. Отже,

С₁= А₁• В₄ + А₂ • В₃ + А₃ • В₂ + А₄ • В₁.

б) Позначимо С₂ = {випаде в сумі хоча б десять очок}. Подія С₂ відбудеться тоді, коли на двох кубиках у сумі випаде або 10, або 11, або 12 очок, тобто і =4, j =6 або і =5, j =5 або і =6, j = 4 або і =6, j =5 або і =5, j =6 або і =6, j =6. Отже

С₂= А₄• В₆ + А₅ • В₅ + А₆ • В₄ + А₆ • В₅. + А₆ • В₆. + А₅ • В₆.

в) Нехай Сз={випаде в сумі не більше трьох очок}. Оскільки найменша кількість очок, яка може випасти на кожному кубику, дорівнює одиниці, то подія Сз можлива лише тоді, коли сума очок на двох кубиках дорівнюватиме двом або трьом. Тому

Сз = А₁ • В₁ + А₂ • В₁ + А₁ • В₂..

Приклад 3. Два стрільці роблять постріл у мішень по одному разу. Позначимо події А = {у мішень влучив перший стрілець}, В = {у мішеньвлучив другий стрілець}. Виразити через А і В такі події: С = {два влучення в мішень} D = {жодного влучення в мішень} Е = {хоча б одне влучення в мішень} F = {лише одне влучення в мішень}.

Розв'язання. Простір елементарних подій складається з чотирьох подій

А • В, • В, А • , • .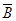

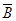Подія С відбудеться тоді, коли обидва стрільці влучать с мішень. Тому вона є добутком двох подій А і В. Отже С = А • В

Подія D полягає в тому, що в мішень не влучить жодний стрілець, тобто не влучить ані перший ( ), ані другий ( ). Тому D =. • .

Подія Е відбудеться тоді, коли влучить хоча б один стрілець. Це може бути толі, коли обидва стрільці влучать с мішень, або влучить перший, але не влучить другий, або не влучить перший, але влучить другий. Тоді

лець. Це може бути тоді, коли або обидва стрільці влучать у мішень, або перший влучить, другий не влучить, або перший не влучить, а другий влучить. Тому

Е = АВ + В + А 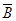, тобто Е = А + В.

Подія F полягає в тому, що перший стрілець влучить в мішень, а другий не влучить, або другий влучить, а перший не влучить. Тому

F = В + А .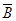

Читайте також:

1. Активні операції банків
2. Активні операції банків з цінними паперами
3. Активні операції комерційних банків
4. Активні операції центральних банків.
5. Алгебраїчні операції
6. Аналітико-конструктивні операції
7. Арифметичні операції
8. Арифметичні операції в різних системах числення
9. Арифметичні операції над цілими числами
10. Баланс підприємства до проведення операції двоступінчастої санації
11. Баланс підприємства після проведення операції двоступінчастої санації, якщо кошти спрямовуються на погашення короткострокових банківських позик.
12. Банк і його операції. Правова природа банківської діяльності

Переглядів: 1634