
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Задачі математичного і лінійного програмування
Тема 1. Задача лінійного програмування
(методичні вказівки № 1358, стор. 3-31)
Задачі математичного і лінійного програмування
Дослідження різних процесів, у тому числі й економічних, звичайно починається з їхнього моделювання, тобто відображення реального процесу через математичні співвідношення. При цьому складаються рівняння або нерівності, які зв'язують різні показники (змінні) досліджуваного процесу та утворюють систему обмежень. У цих співвідношеннях виділяються такі змінні, змінюючи які можна одержати оптимальне значення основного показника даної системи (прибуток, доход, витрати й т.п.). Відповідні методи, що дозволяють вирішувати зазначені задачі, об'єднуються під загальною назвою "математичне програмування" або "методи дослідження операцій".
Математичне програмування містить у собі такі розділи математики, як лінійне, нелінійне й динамічне програмування. Сюди відносять також стохастичне програмування, теорію ігор, теорію масового обслуговування, теорію керування запасами й деякі інші.
Отже, математичне програмування – це розділ вищої математики, присвячений розв'язанню задач, пов'язаних зі знаходженням екстремумів функцій кількох змінних при наявності обмежень на змінні.
Математичне програмування виникло в 30-і роки ХХ ст. Угорський математик Б. Егерварі в 1931 році розв’язав задачу, названу "проблемою вибору". Американський учений Г. Кун узагальнив цей метод, після чого він став називатися "угорським" методом. В 1939 р. російський учений Л. В. Конторович розробив метод розв'язуючих множників розв'язання задач лінійного програмування. Великий внесок у розвиток математичного програмування внесли американські вчені. В 1947 р. американський учений Дж. Данут описав один з основних методів розв'язання задач лінійного програмування, що одержав назву “симплексний”.
Побудова математичної моделі економічної задачі включає наступні етапи: 1) вибір змінних задачі; 2) складання системи обмежень; 3) вибір цільової функції.
Змінними задачі називаються величини 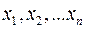 , які повністю характеризують економічний процес. Їх звичайно записують у вигляді
, які повністю характеризують економічний процес. Їх звичайно записують у вигляді 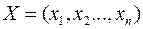 .
.
Система обмежень містить у собі систему рівнянь і нерівностей, яку задовольняють змінні задачі і які випливають із обмеженості ресурсів або інших економічних та фізичних умов, наприклад, умови позитивності змінних і т.п.
Цільовою функцією називають функцію змінних задачі, що характеризує якість виконання задачі, і екстремум якої потрібно знайти.
Загальна задача математичного програмування формулюється так: знайти екстремум цільової функції
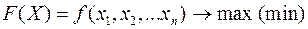 (1)
(1)
і відповідні йому значення змінних за умови, що ці значення задовольняють систему обмежень
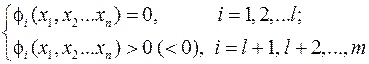 (2)
(2)
Якщо цільова функція (1) і система обмежень (2) лінійні, то задача математичного програмування називається задачею лінійного програмування (ЗЛП).
У загальному випадку ЗЛП може бути записана у вигляді:
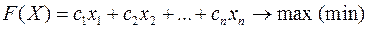 (3)
(3)
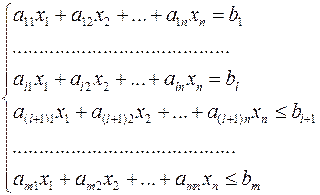 (4)
(4)
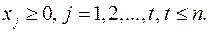 (5)
(5)
Даний запис означає наступне: знайти екстремум цільової функції задачі (3) і відповідні йому значення змінних 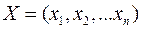 за умови, що ці значення задовольняють систему обмежень (4) і умови невід’ємності (5).
за умови, що ці значення задовольняють систему обмежень (4) і умови невід’ємності (5).
Допустимим розв'язком (планом) ЗЛП називається будь-який n-мірний вектор 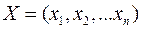 , що задовольняє систему обмежень й умови невід’ємності.
, що задовольняє систему обмежень й умови невід’ємності.
Множина допустимих розв'язків (планів) задачі утворює область допустимих розв'язків (ОДР).
Оптимальним розв'язком (планом) ЗЛП називається такий допустимий розв'язок (план) задачі, при якому цільова функція досягає екстремуму.
Так як у цьому випадку розв’язується задача на екстремум, то виникає питання: чи можна використовувати класичні методи дослідження на екстремум функції багатьох змінних. Застосуємо необхідну умову екстремуму функції, яка полягає в тому, що часткові похідні функції багатьох змінних або дорівнюють нулю, або не існують. У цьому випадку
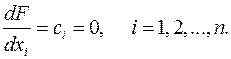
Але якщо всі 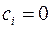 , то і
, то і 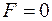 , тобто екстремум функції не досягається. Пов'язано це з тим, що похідну можна використати для визначення екстремуму тільки у внутрішніх точках області розв'язання, а в цьому випадку екстремум, як буде показано далі, знаходиться на межах області. Звідси й виникає необхідність розробки спеціальних методів пошуку екстремуму.
, тобто екстремум функції не досягається. Пов'язано це з тим, що похідну можна використати для визначення екстремуму тільки у внутрішніх точках області розв'язання, а в цьому випадку екстремум, як буде показано далі, знаходиться на межах області. Звідси й виникає необхідність розробки спеціальних методів пошуку екстремуму.
Читайте також:
- А) Задачі, що розкривають зміст дій
- Алгебраїчне та інсерційне програмування
- Алгоритм розв’язання задачі
- Алгоритм розв’язання задачі
- Алгоритм розв’язання розподільної задачі
- Алгоритм розв’язування задачі
- Алгоритм розв’язування задачі
- Алгоритм розв’язування задачі
- Алгоритм розв’язування задачі
- Алгоритм розв’язування задачі
- Алгоритм розв’язування задачі
- Алгоритм розв’язування задачі оптимізації в Excel
| <== попередня сторінка | | | наступна сторінка ==> |
| Організація місцевої роботи на підрозділах залізничного транспорту | | | Математична модель задачі про використання сировини. |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |