• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

ЕЛЕМЕНТИ КЛАСИФІКАЦІЇ ЗАДАЧ СТОХАСТИЧНОГО ПРОГРАМУВАННЯ

Розділ 7. ЕКОНОМІЧНИЙ РИЗИК ТА ДЕЯКІ МОДЕЛІ І МЕТОДИ СТОХАСТИЧНОГО ПРОГРАМУВАННЯ

Основні терміни: стохастичне програмування, прямі методи, непрямі методи, адаптивність.

ЗАГАЛЬНІ ПОЛОЖЕННЯ.

ЕЛЕМЕНТИ КЛАСИФІКАЦІЇ ЗАДАЧ СТОХАСТИЧНОГО ПРОГРАМУВАННЯ

Наявність стохастичної невизначеності вносить у планування та прийняття економічних рішень елемент ризику.

Для підприємств, які працюють за ринкових умов, вста­новлення внутрішнього плану (програми), як правило, супро­воджується укладенням контрактів з оптовими споживачами, причому порушення контракту призводить не тільки до явних економічних неприємностей для підприємства (корпорації) у вигляді штрафів, але і до непрямих наслідків, що йменуються «втрата інтересу і пріоритетності споживачів». Завжди мають місце дві тенденції, що вступають у протиріччя: з одного боку, прагнення до збільшення обсягу зобов'язань, тобто у кінце­вому рахунку до збільшення валового обсягу запрограмовані продукції чи прибутку, з іншого боку, прагнення до змен­шення ризику невиконання зобов'язання через несприятливі зовнішні та внутрішні обставини протягом планового періоду.

Стохастичним програмуванням називають розділ математич­ного програмування, що вивчає теорію, моделі й методи розв'я­зування умовних екстремальних задач за неповної інформації щодо параметрів умов задачі.

Предметом стохастичного програмування є умовні екстре­мальні задачі, де параметри умов чи складові розв'язку, або усі вони разом, є випадковими величинами.

Постановка задач стохастичного програмування суттєво зале­жить від цільових засад та інформаційної структури задачі.

Одна з постановок задачі керування і, зокрема, планування за умов невизначеності та ризику полягає у наступному.

Припустимо, що вектор „х” позначає можливі рішення (альтер­нативи) з деякої апріорно допустимої множини X. Раціональний вибір рішень здійснюється з наслідків, до яких призводять ці рішення. Але наслідки рішення залежать не лише від обраного вектора 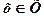, але й від випадкових чинників (параметрів), котрі позна­чають через "ω". Значення "ω" заздалегідь невідомі. Вважають, що відома множина „Ω”, до якої належить вектор "ω". Відносно розподілу "ω"на множиш Ω можуть бути різні гіпотези. У кращому разі відомий точний закон розподілу "ω", у гіршому — лише те, що .

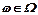Зв'язок між рішенням „х” та наслідками записують у виді функціональної залежності f(x, ω), яка називається моделлю.

Моделями можуть бути алгебраїчні співвідношення з випад­ковими параметрами, стохастичні диференційні рівняння, марковські процеси та інші.

Являє інтерес класифікація задач стохастичного програму­вання, що виникають за умов ризику та невизначеності за показником якості (ефективності) розв'язку.

Природно розглядати наступні показники якості розв'язку стохастичних задач, зокрема лінійних:

• математичне сподівання величини лінійної форми;
• дисперсія лінійної форми;
• лінійна комбінація математичного сподівання та дисперсії лінійної форми;
• ймовірність перевищення лінійною формою певного фік­сованого порогу;
• математичне сподівання корисності лінійної форми;
• максимін лінійної форми (причому максимум береться з множини планів X, а мінімум за допустимими значеннями 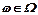набору параметрів, що визначають реалізацію випадкових елементів умов задачі) тощо.

Задачі стохастичного програмування розподіляють також на статичні та динамічні.

Для того, щоб задача стохастичного програмування мала сенс, необхідно відповісти на наступні три запитання:

1. Як розуміти вектор лі? Чи повинен він також бути випад­ковим (тобто кожному "ω" відповідає своє рішення х(ω), що визначається, скажімо, стандартними правилами лінійного програмування), чи детермінованим, що не змінюється при випад­кових варіаціях параметрів моделі?

2. Як розуміти максимізацію цільової функції? Як максимізацію абсолютну, для усіх 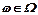чи максимізацію її матема­тичного сподівання, чи максимізацію деякої іншої її ймовір­нісної характеристики?

3. Як розуміти виконання обмежень: абсолютно для всіх 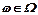чи у середньому, чи допускати їх порушення з малою ймовірністю тощо?

Під час вирішення цих питань доводиться виходити не лише з математичних міркувань, а й з економічного змісту та еврис­тичних міркувань, котрими необхідно керуватися при дослід­женні та моделюванні систем з ризиком.

Постановки задач стохастичного програмування, що вини­кають при моделюванні економічного ризику, суттєво залежать від того, чи є можливість при виборі (прийнятті) рішень для уточнення стану економічного середовища через певні спо­стереження чи ні. Так, коли проводиться перспективне планування, рішення приймається перед тим, як будуть зроблені спостереження за станом середовища (скажімо, стануть відомими потреби) й рішення (розв'язок) буде детермінованим. У задачах оперативного чи поточного планування рішення приймаються після певних спостережень (експериментів) над станом економічного середовища залежно від результатів спостережень і тому бувають стохастичними (варіантними).

Якщо в результаті спостереження стан економічного середовища стає відомим, то вибір рішення (розв'язку) х(ω) при заданому 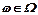зводиться до звичайної задачі нелінійного програмування. Наприклад, мінімізувати (максимізувати):

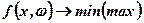(7.1)

при врахуванні обмежень

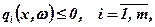(7.2)

а також умов

(7.3)

Лінійну одноетапну модель стохастичного програмування можна подати у матрично-векторній формі:

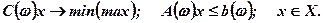
Відзначимо, що у загальному випадку спостереження не повністю визначають стан економічного середовища, тому етапи вибору рішень можуть чергуватися з етапами спостережень над станом економічного середовища. Тобто, мають місце багато-етапні процеси вибору рішень, кожне з яких може розвиватися за двома низками:

рішення — спостереження — рішення — ... — спостережен­ня — рішення;

спостереження — рішення — спостереження — ... — спостере­ження — рішення.

Низка рішень називається N-етапною, якщо слово «рішення» зустрічається N разів.

Якщо рішення х детерміноване і приймається перед тим, як спостерігається стан середовища "ω", то співвідношенням (7.1) ... (7.3) слід надати певний імовірнісний зміст, бо для фіксованого х для одних 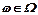співвідношення (7.2) можуть виконуватися і х виявиться допустимим розв'язком, а для інших 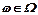можуть не виконуватися. У більшості випадків є сенс у максимізації (мінімізації) математичного сподівання f(x, ω), тобто, необхідно відшукати такий вектор х, за якого досягається екстремум функ­ції Мf(x, ω):

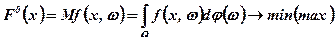(7.4)

за умов

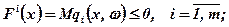(7.5)

(7.6)

Функцію F⁰(x) називають функцією ризику, а 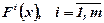-функцiями регресії; φ(ω) — щільність розподілу.

Як вже відзначалося, математичне сподівання функції f(x,ω) не єдина ймовірнісна характеристика. Розглядають також дисперсію функції f(x,ω), чи моменти вищих порядків випадкової величини f(x, ω), їх алгебраїчні суми зважені за допомогою деяких коефіцієнтів, зокрема:

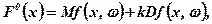(7.7)

де k - ціна ризику.

Приведемо приклади задач стохастичного програмування, що виникають за умов ризику.

Приклад. Вибір запасів. Потрібно зробити запас з п товарів у кількості (х₁, х₂, ...,х_n), на які є випадковий попит (ω₁, ω₂, ..., ω_n) = ω. Нестача запасених товарів штрафується з коефіцієн­тами (с₁, с₂,..., с_n) = с, а затрати на зберігання одиниці продук­ції, яку не вдалося збути, задаються вектором (d₁, d₂, ..., d_n) = d.

Розв'язання. Функція збитків, що відповідає розв'язку х, має вид:

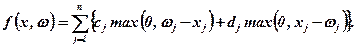(7.8)

Приклад. Вибір поставляння інгредієнтів. Виробнича система виробляє з певних інгредієнтів деякий продукт. Розглянемо виробничу функцію f(x) = f(x₁, х₂, ...,x_n) цієї системи, що від­биває кількість продукту при виробництві з п інгредієнтів у кількості х₁, х₂, ..., х_n відповідно.

Розв'язання. Як правило, у математичній економіці (економіксі) приймається припущення, що виробничі функції квазіугнуті за сукупністю аргументів. Наприклад, угнутою є комп­лектна виробнича функція:

(7.9)

де а₁, a₂, ..., а_n — виробничі константи (комплект). Відома 1/п угнута — виробнича функція Кобба-Дугласа:

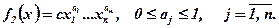(7.10)

Частина інгредієнтів (компонент) у цих функціях може виби­ратися у детермінованих кількостях, а решта визначається випад­ковими поставками, тому у загальному випадку можна вважати, що виробнича функція f(x, ω) залежить від детермінованого х та випадкового (ω) векторів і є квазіугнутою, 1/n угнута за сукупністю змінних (x, ω).

Приклад. «Портфельний» підхід до теорії грошей [59]. У формальній кейсіанській моделі індивіди можуть тримати своє багатство (індивідуальні портфелі) у вигляді грошей та облі­гацій. Гроші — це актив, що використовується як засіб обігу та не приносить відсоткової ставки, облігації — цінні папери, які дають певний відсоток.

Чому ж люди не зберігають своє багатство повністю у вигляді облігацій? Економісти пояснюють це наявністю невизначеності та небажанням надміру ризикувати, бо відсоток та ринкова вартість облігацій наперед точно не відомі.

Розв'язання. Введемо позначення: S — величина активу, х та у — величини активу, що зберігаються відповідно у формі грошей та облігацій. Вважається, що через рік активи, вкладені в облігації, змінюються. При решті рівних умов облігацію, що приносить більший відсоток прибутку, на ринку цінних паперів можна збути за більшу ціну, ніж облігацію з меншим відсотком. Позначимо через k та "ω" величини активів, які реалізуються через рік на одиницях активів, відповідно залишених у формі грошей та вкладених в облігації. Для нашого прикладу k = 1, а "ω" є випадковою величиною. Якщо 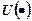— функція корисності, визначена щодо величини активу через рік, то модель найбільш пріоритетного розподілу активу на гроші та облігації полягає у максимізації сподіваної корисності:

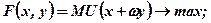(7.11)

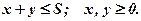(7.12)

У випадку нейтрального ставлення особи, що приймає рі­шення, до ризику вираз (7.11) має вид:

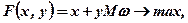(7.13)

і питання щодо розподілу активу між грішми та облігаціями вирішиться повністю на користь одного з цих видів залежно від знаку різниці (Мω – 1). Якщо Мω > 1, то вкладення повністю здійснюються в облігації, у протилежному випадку — актив збе­рігається повністю у формі грошей.

Аналіз ускладнюється при небайдужості до ризику особи, яка приймає рішення.

Приклад. Модель оптимізації розподілу внесків в ощадний та комерційний банки [59]. У комерційних банках нарахо­вується більший відсоток на вкладені суми порівняно з ощад­ними, але внесок не гарантується. Перед кожним вкладником постає дилема: мати меншу, але гарантовану суму, або більшу, проте з ризиком втратити і сам внесок. З ризиком невикористаних можливостей пов'язаний і внесок в ощадний банк.

Розв'язання.Позначимо через „s” загальну суму грошових коштів певного власника; х — внесок в Ощадбанк, у — в комер­ційний; a, b — відсоток нарахування відповідно в ощадному та комерційному банках; (1-р) — імовірність вилучення внесків у комерційному банку внаслідок його ліквідації (банкрутства); 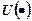— функція корисності власника. Джерелом невизначеності в цьому прикладі екомерційний банк.

При розподілі S на х та у можливі такі дві ситуації щодо отримання дивідендів:

ах+ by — за умови успішного функціонування комерційного банку;

ах - у — у протилежному випадку.

Модель оптимізації розподілу грошей між банками матиме вид:

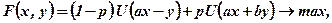(7.14)

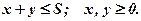(7.15)

Приклад. Оптимальне страхування [59]. Страхування — один із засобів, що пом'якшує негативні наслідки ризику, що пов'я­заний, зокрема, з коливаннями кон'юнктури ринку. Слід оціню­вати витрати на страхування і його корисний ефект. Нехай, у спрощеній інтерпретації, особа бажає застрахувати певну частку свого активу. Для цього сплачує певний внесок страховій ком­панії, а у випадку втрати активу отримує від неї страхову вина­городу. Треба визначити частку активу, яку особа вважає доціль­ним застрахувати.

Розв'язання. Позначимо через S актив (капітал, майно тощо), власником якого є певна особа. Частку, яку бажано застрахувати, позначимо через х. Страховий внесок, що сплачується страховій компанії, має значення rx, а у випадку втрати активу особа, що застрахувалася, отримує винагороду qx. Якщо клієнт має інформацію про ймовірність недоторканості свого активу р, то модель визначення частки страхового активу має вид:

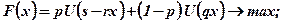(7.16)

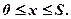(7.17)

Тут 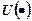— функція корисності власника активу.

Модель клієнта (7.16), (7.17) може бути корисною й для страхових компаній при визначенні доцільних величин стра­хових винагород, які б зацікавлювали клієнтів та були вигідними для страхової компанії.

Приклад. Балансування сировинної бази та переробної про­мисловості [59]. Розглянемо однопродуктовий агропромисловий комплекс (цукровий), у розвиток якого вкладаються певні кошти.

Ці кошти можуть розподілятися у певній пропорції на роз­виток сировинної бази та потужностей по її переробці. Треба так спланувати розподіл коштів, щоб отримати найбільшу кіль­кість кінцевої продукції (у нашому випадку — цукру). При цьо­му урожайність культури (цукрових буряків) вважається випад­ковою величиною.

Розв'язання. Нехай "ω"— урожайність культури, S — обсяг коштів; q₁ — питомі затрати коштів на обробку площі, де ви­рощується культура; q₂ — питомі зведені затрати на створення потужностей по переробці; d — частка виходу кінцевої про­дукції з одиниці сировини; х — площа, що обробляється; у — потужності по переробці. Необхідно максимізувати сподіваний обсяг кінцевої продукції при обмежених коштах S, тобто:

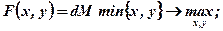
Читайте також:

1. I. Застосування похідної та інтеграла до роз’язування задач елементарної математики.
2. II. Елементи операційних витрат
3. А) Задачі, що розкривають зміст дій
4. АВТОМАТИЗАЦІЯ РОЗВ’ЯЗУВАННЯ КОМПЛЕКСУ ЗАДАЧ З ОБЛІКУ ОСНОВНИХ ЗАСОБІВ ТА НЕМАТЕРІАЛЬНИХ АКТИВІВ
5. Аграрна структура та її елементи
6. Адміністративне правопорушення як підстава юридичної відповідальності: ознаки і елементи
7. Адміністративне правопорушення як підстава юридичної відповідальності: ознаки і елементи.
8. Азот, фосфор, біогенні елементи та їх сполуки, органічні речовини
9. АКУСТИКА. ЕЛЕМЕНТИ ФІЗИКИ СЛУХУ. ОСНОВИ АУДІОМЕТРІЇ
10. Алгебраїчне та інсерційне програмування
11. Алгоритм розв’язання задачі
12. Алгоритм розв’язання задачі

Переглядів: 767