• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

ПРАВОМІРНІСТЬ ПРИЙНЯТТЯ РІШЕНЬ ЗА УМОВ РИЗИКУ НА БАЗІ СПОДІВАНИХ ЗНАЧЕНЬ ВИПАДКОВИХ ПАРАМЕТРІВ

Природний на перший погляд такий аналіз задач стохастичного програмування — заміна випадкових величин с(ω), А(ω), b(ω) їх середніми значеннями та визначення оптимальних планів на основі детермінованих задач. Цей підхід не завжди призводить до прийнятного розв'язку та не враховує ризику. Нехай масив (с, А, b) у моделі (7.1) ... (7.3) складається з випадкових величин, тобто залежить від "ω" — випадкової ситуації чи елементарної події деякого ймовірнісного простору (Ω, А, Р), где Ω — множина елементарних подій, А – Ω — алгебра подій, визначена на цій множині, Р — імовірнісна міра.

Замінюючи компоненти с(ω), А(ω), b(ω) їх математичними сподіваннями, розглянемо задачу:

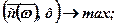(7.18)

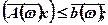(7.19)

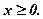(7.20)

Визначення плану з (7.18) ... (7.20) еквівалентне припущенню, що під час прийняття рішення використовуються сподівані (се­редні) значення випадкових параметрів. У яких випадках право­мірна така заміна? Відповісти на це запитання можна простим прикладом. Нехай результат ефективності функціонування сис­теми "η"залежить лише від дії на неї випадкових чинників, тобто 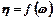. Отже, функція "η"є випадковою величиною та має закон розподілу, що залежить від закону розподілу випадкової ве­личини "ω". Перевіримо, чи буде виконуватися рівняння:

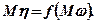(7.21)

Якщо функція η лінійна відносно ω тобто η = а + bω, то 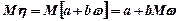і рішення (7.21) буде коректним.

Якщо функція η нелінійна, наприклад, η = ω², 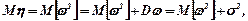тобто рівняння (7.21) несправедливе, має місце зміщення на "σ²". Таким чином припущення щодо можли­вості заміни випадкової величини її математичним сподіванням у загальному випадку невірне.

Наявність балансу у середньому зовсім не означає узгодження витрат ресурсів з їх реальною наявністю. План, обраний згідно з (7.18) ... (7.20) у більшості випадків може виявитися нереальним, надто ризикованим. Тому спосіб такого штучного зведення стохастичної моделі до детермінованої та розв'язок останньої засто­совують переважно у грубих, орієнтовних розрахунках, а також у тих випадках, коли діапазон можливих значень випадкових ве­личин та їх дисперсії відносно малі, тобто вони можуть розгля­датися, але з певними застереженнями, як детерміновані вели­чини [22]. Характеристикою розсіювання випадкового параметра "ω" може бути коефіцієнт варіації цієї випадкової величини, що визначається як σ/Мω, де 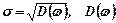— дисперсія величини ω, Мω — математичне сподівання "ω".

ВИБІР НАЙКРАЩОГО ПЛАНУ ТА ДОСЛІДЖЕННЯ ЗОНИ НЕВИЗНАЧЕНОСТІ

Зоною невизначеності називається сукупність оптимальних планів, залежних від випадкової ситуації "ω", тобто зона неви­значеності — це [59]. Вона може бути апроксимована скінченою кількістю оптимальних планів 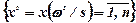, яку одержують на базі статистичного моделювання за мето­дом Монте-Карло, та числового розв'язку для кожного ω = ω^s задачі:

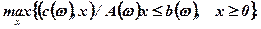(7.22)

Розв'язок цієї задачі позначимо через х(ω), тобто:

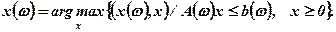(7.23)

При цьому величина п повинна бути досить великою.

Використовуючи різні неформальні процедури, домагаються звуження апроксимації зони невизначеності та більш чіткого ви­значення множини, що містить у собі шуканий план. Позначають звужену апроксимацію зони невизначеності через 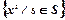, де S — підмножина {1,...., n} множини. З аналізу пристосованості кожного варіанта плану до зміни умов відбувається остаточний вибір шуканого плану. Кожен план x^s коригується за допомогою наперед визначеної множини адаптивних технологій D(ω), шля­хом вибору їх інтенсивностей, що описуються вектором у.

Адаптивність — це здатність економічної системи присто­совуватися до змін внутрішніх і зовнішніх умов.

Якщо d(ω) — вектори (стовпчики) питомих ефективних технологій матриці D(ω), то при фіксованих „х” та "ω" доцільно обрати план у як розв'язок задачі:

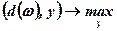(7.24)

за умов

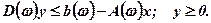(7.26)

Розв'язок задачі (7.24)...(7.25) позначають через у(х,ω). Звужена апроксимація зони невизначеності разом з планами адаптивних технологій записується у виді:

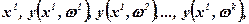
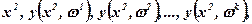(7.27)

…………………………………………………………..

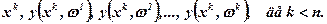
При виборі найкращого (раціонального) плану береться до уваги не лише ефективність основного плану x^s, але й ефек­тивність відповідної адаптації при різних ω.

Даний метод має такі особливості:

1) відбувається глибоке зондування за допомогою методу статистичних випробувань Монте-Карло всієї множини випад­кових ситуацій з врахуванням імовірнісного розподілу випад­кових параметрів;

2) припускається можливість коригування (адаптації) раніше обраного плану згідно з надходженням інформації щодо реа­лізації випадкових ситуацій;

3) здійснюється найбільш ефективна адаптація для кожної реалізації випадкових ситуацій.

Читайте також:

1. I. Доповнення до параграфу про точкову оцінку параметрів розподілу
2. III. Сприйняття й засвоєння учнями навчального матеріалу
3. IV. Прийняття рішень у полі четвертої інформаційної ситуації
4. IV. Сприйняття та усвідомлення навчального матеріалу
5. V. Прийняття рішень у полі п’ятої інформаційної ситуації
6. VI. Прийняття рішень у полі шостої інформаційної ситуації
7. Абсолютна величина можливих значень
8. Абстрактна небезпека і концепція допустимого ризику.
9. Адміністративна та судова процедура оскарження рішень податкових органів
10. Акти прийняття продукції за якістю і кількістю
11. Алгебра випадкових подій
12. Алгоритм прийняття рішення при прийманні сигналів з випадковою початковою фазою

Переглядів: 369