• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

ЗАГАЛЬНА МОДЕЛЬ ПРИЙНЯТТЯ АДАПТИВНИХ РІШЕНЬ ЗА УМОВ РИЗИКУ

Прийняття рішень за умов ризику, що здійснюється за схе­мою: «рішення — спостереження — рішення» є найбільш роз­повсюдженим у науковій літературі стосовно стохастичного прог­рамування. На базі цієї схеми будуються двохетапні стохастичні моделі планування.

У ряді праць, зокрема в [59], відзначається, що ця схема включає такі вимоги до плану, як необхідність жорсткості певних його параметрів та можливість часткової пристосо­ваності (адаптації) плану до внутрішніх та зовнішніх випад­кових змін.

Програмна частина обирається з урахуванням того, що необ­хідно створювати найкращі умови для майбутньої адаптації і розрахована на ймовірні зміни випадкових ситуацій. Адаптивна частина реалізується після спостереження, тобто враховується вплив реалізації випадкового стану економічного середовища (ситуації). Використовуючи позначення: х — програмна частина плану, "ω" — параметри випадкової ситуації, у — адаптивна час­тина плану, схему можна подати у виді:

х – ω – у(х, ω). (7.28)

Нехай (х, у) — план певної економічної системи, що оби­рається з допустимої множини планів Х(ω), де ω — випадкова ситуація (елементарна подія певного ймовірнісного простору (Ω, Ф, Р). Суб'єкт керування (прийняття рішень), зацікавлений упевних результатах, які залежать від невизначеної (випадкової) ситуації і можуть бути представлені вектор-функцією f(х, у, ω) = (f₁(х, у, ω), ..., f_m(x, y,ω)).

Припустимо, що для будь-якої пари планів [х¹, у¹] та [х², у²], суб'єкт керування може надати перевагу одному з розподілів L(f, x¹, y¹, Ω, P), L(f, x², y², Ω, P), або визначити їх еквівалентність, тобто на множиш розподілів задано відношення пріоритетності — не гірше ніж). Тут через L(f, x, y, Ω, P), позначений розподіл f(х, у, ω), який залежить від х, у на множині елементарних подій 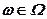та ймовірнісній мірі Р.

Якщо обрана певним чином програма х і відбулося спостере­ження над реалізацією випадкової ситуації 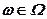, то задача вибору найефективнішої адаптації для даної ситуації ω полягає в знаходженні такого у, при якому:

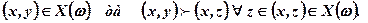
Введемо позначення розв'язку задачі знаходження найефек­тивнішої адаптації [59]:

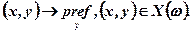(7.29)

Розв'язок (7.29) залежить як від обраного раніше (на попе­редній стадії) х, так і від ω, тобто у = у(х, ω).

У свою чергу, на першій стадії рішень двохетапної задачі, тобто при виборі плану-програми х, необхідно серед допустимих розв'язків знайти таке х, при якому розподіл f, залежний від х і найкращої адаптації у(х, ω) для кожної реалізації ситуації 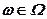, був би найбільш пріоритетним для суб'єкта керування. Тобто, необхідно знайти 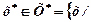з імовірністю 1 існує 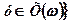, при якому

(7.30)

Задачу знаходження х* позначають так:

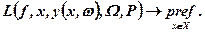(7.31)

Читайте також:

1. CMM. Модель технологічної зрілості. Зрілі і незрілі організації.
2. Demo 7: Модель OSI (модель взаімодії відкритих систем)
3. G2G-модель електронного уряду
4. I. Загальна характеристика політичної та правової думки античної Греції.
5. III. Сприйняття й засвоєння учнями навчального матеріалу
6. IV. Загальна оцінка діяльності вчителя
7. IV. Загальна схема поточного і підсумкового контролю та оцінювання знань студентів
8. IV. Прийняття рішень у полі четвертої інформаційної ситуації
9. IV. Сприйняття та усвідомлення навчального матеріалу
10. Ni - загальна кількість періодів, протягом яких діє процентна ставка ri.
11. OSI - Базова Еталонна модель взаємодії відкритих систем
12. V – модель

Переглядів: 369