• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

ОДНОЕТАПНІ СТАТИЧНІ ЗАДАЧІ УПРАВЛІННЯ ВИРОБНИЦТВОМ ЗА УМОВ РИЗИКУ

Під статичними моделями розуміють такі, всі параметри яких протягом всього періоду управління залишаться незмін­ними, або ж їх зміною можна знехтувати. Вивчення статичних моделей доцільне, зокрема, коли необхідно встановити почат­ковий рівень виробництва нових товарів, що є відправним етапом для подальшого розв'язку динамічних задач управління виробництвом.

В одноетапних задачах нехтують також динамікою надход­ження інформації, рішення приймаються на основі інформації, яка існує на момент прийняття рішення на початку інтервалу (періоду) управління (планування).

Рішення за цих умов є детермінованим.

Розглянемо виробничо-економічну систему з певною потуж­ністю (тут термін «потужність» можна замінити допустимим обсягом виготовлюваної продукції за одиницю часу), в якій треба визначити рівень (обсяг) виробництва деяких продуктів (набору продуктів) х, попит на які на ринку (у споживача) заздалегідь не відомий і вважається випадковою величиною 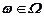.Позначимо через q(х) — величину загальних затрат при вироб­ництві продукції. Позначимо також через f¹(x, ω) збитки, яких зазнає виробництво від недовипуску продукції, коли 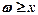, а через f²(x, ω) — збитки, які виникають у тому разі, коли вироб­ництво перевищує величину випадкового попиту, тобто, коли х > ω. Ці випадки відображує функція виду:

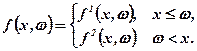
Нехай функції f¹ та f² при кожному "ω" є опуклими вниз та неперервно диференційованими по х.

Таким чином, задача полягає у знаходженні такої кількості товару х, який мінімізує сумарні сподівані затрати, що скла­даються із вартості виробництва, тобто:

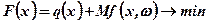(7.32)

при обмеженнях

(7.33)

Тут X — деяка множина n-мірного простору, яка може бути утворена обмеженням, пов'язаним з потужністю підприємства, обсягами продукції. У випадку, коли максимізується прибуток від реалізації продукції, що виробляється:

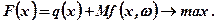
Типові труднощі, що виникають при розв'язуванні одно­етапної задачі (7.32), (7.33), полягають у складності (або немож­ливості) точного обчислення значень функції сподіваних витрат F(х) та її градієнта, що пов'язане з обчисленням інтегралу виду:

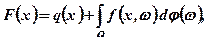
де φ(ω) — функціярозподілу випадкового параметру.

Додаткові труднощі виникають при не диференційованості функції f(x, ω).

Ці особливості обумовлюють необхідність створення спе­ціальних моделей, орієнтованих на розв'язування задач виду (7.32), (7.33), які звичайно поділяються на два класи: непрямі методи, що полягають у зведенні до задачі, яку можна розв'язати за відомими методами класичного аналізу та нелінійного про­грамування; та прямі методи, що дозволяють розв'язати задачу «в лоб», з використанням доступної інформації про спосте­реження реалізації f(x, ω) в деяких фіксованих точках .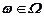

7.5.1. НЕПРЯМІ МЕТОДИ РОЗВ'ЯЗАННЯ ОДНОЕТАПНОЇ ЗАДАЧІ

Залежно від того, чи зводиться одноетапна стохастична задача управління виробництвом (7.32), (7.33) до еквівалентної щодо неї задачі, чи до задачі, розв'язання якої в деякому сенсі близьке до вихідної, непрямі методи розв'язування стохастичних задач управління виробництвом можуть грунтуватися на застосуванні необхідних та достатніх умов екстремуму та параметризації рішення, або наближеній заміні закону розподілу випадкового параметра, на використанні детермінованого аналізу стохастичної моделі.

Непрямі методи, як правило, дають непогані результати для обмеженого класу задач, специфіку яких вони враховують, зупи­нимося на деяких з них.

Застосування класичного аналізу. Припустимо, що в задачі (7.32), (7.33) функція цілі F(x) опукла, f(x, ω) — диференційована майже при всіх значеннях ω.Необхідною та достатньою умовою того, щоб точка х* була рішенням такої задачі, буде:

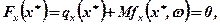(7.34)

де 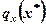— градієнт функції q (х) в точці х*; f_х (x^*,ω) — градієнт функції f(x,ω) по х уточці (x^*,ω); F_x(x*) —градієнт функції F(x).

У випадку, коли відома функція розподілу випадкових параметрів "ω", система (7.34), може бути розв'язана аналітичними методами.

Такий підхід, як правило, використовується для розв'язу­вання задач малої розмірності і в тому випадку, коли необхідно знайти безумовний мінімум функції затрат F(x). Під час засто­сування для розв'язування одноетапної задачі управління вироб­ництвом наштовхуються на такі труднощі.

По-перше, не у всіх прикладних задачах можлива точна побу­дова функції розподілу φ(ω). У деяких, наприклад, коли вона являє собою функцію випадкових параметрів, що спостерігаються впер­ше, така побудова практично неможлива. Інколи перепоною для побудови φ(ω) стає малий обсяг статистичної вибірки.

По-друге, цільова функція (7.32) в загальному випадку негладка.

Все це звужує межі застосування даного підходу.

Детермінований аналог. Часто стохастичну задачу намагають­ся замінити детермінованою, вибраною так, щоб її розв'язок або співпадав з розв'язком вихідної задачі (тоді така модель нази­вається детермінованим аналогом), або був близьким до нього. Якби в задачі (7.30), (7.33) була точна інформація про попит у розглядуваному періоді, тоді оптимальний рівень виробництва х* дорівнював би відомому попитові, тобто х^* = ω.

Але обсяг попиту попередньо не відомий, він випадковий.

Часто на практиці півень виробництва розраховується з се­реднього попиту 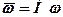, тобто мінімізують функцію 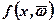, де 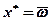, тобто задача виявляється тривіальною. Правомірність цього була розглянута в 7.2.

При такому підході не враховуються основні особливості проблем управління виробництвом, пов'язані з надвиробницт­вом або недовиробництвом продукції порівняно з попитом.

Таким чином задача (7.32), (7.33) має сенс тільки в стохастичній постановці, коли необхідно визначити рівень виробницт­ва, найбільш стійкий до можливих змін випадкового попиту.

Наближене інтегрування. Припустимо, що обчислення функції ризику пов'язане з обчисленням n-кратного інтеграла:

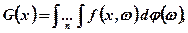
де φ(ω) — функція спільного розподілу випадкового вектора ω.

Розв'язати цю задачу аналітичними методами не завжди є можливим.

При обчисленні даного інтеграла можна використати детер­міновані наближені числові методи інтегрування, але для досить великого n цей підхід неприйнятний. У такому випадку оцінки інтеграла можна одержати за методом Монте-Карло згідно з формулою:

(7.35)

де — незалежні, однаково розподілені випадкові величини, тобто згенеровані відповідно з заданою функцією розподілу φ(ω).

Дійсно, G (х) — середнє значення функції, тобто останній вираз є оцінкою цього середнього значення на базі n-спостережень над величиною попиту , тобто, воно може бути наближеним значенням. Тому застосування методу Монте-Кар­ло для наближеного обчислення значень функцій ризику з наступним їх застосуванням в обчислювальних схемах методів нелінійного програмування призводить до розгляду принципово нових методів математичного програмування, що ґрунтуються на використанні статистичних оцінок значень та градієнтів функ­ції, яка мінімізується. Саме вони стали основою прямих методів стохастичного програмування для розв'язування задач управ­ління виробництвом.

7.5.2. ПРЯМІ МЕТОДИ РОЗВ'ЯЗУВАННЯ ОДНОЕТАПНОЇ ЗАДАЧІ

Прямі методи рішення стохастичної задачі управління вироб­ництвом (7.32), (7.33) оперують лише значеннями f(x,ω), їх прин­ципові алгоритми не змінюються із зміною закону розподілу по­питу ω, не потребують знання цих законів в явному виді, тобто вони застосовуються під час розв'язування складних задач, де випадковість задається лише імітаційною моделлю.

Ці методи відносно прості для числової реалізації, економно використовують оперативну пам'ять ЕОМ. Вони дозволяють виконувати обчислення в режимі діалогу та враховувати специ­фіку розв'язуваної задачі [20, 22, 27, 28, 56, 59]. Великий перелік прямих методів стохастичного програмування побудований на основі ітеративних методів, які використовують узагальнений квазіградієнт (субградіент, узагальнений градієнт) [20].

Найпоширенішими прямими методами стохастичної оптимізації є методи стохастичних квазіградієнтів з проектуванням та стохастичної лінеаризації. Стосовно задачі (7.32), (7,33) ці методи являють собою алгоритм побудови послідовності {х^s} — набли­жень до оптимального розв'язку задачі.

Розглянемо алгоритм [20]. Нехай на s-му кроці (ітерації) одержано наближене x^s, s = 0, 1, ... (х⁰ — задане довільне почат­кове наближення).

1. Відповідно з апріорним розподілом φ(ω) одержуємо спостереження ω^s над реалізацією випадкової величини "ω". Зауважи­мо, що для цього можна використати імітаційну модель.

2. Побудуємо векторстохастичного квазіградієнта функції :

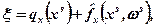
де q_x (x^s) — градієнт функції q(х) в точці x^s; 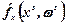— узагальнений градієнт функції f(x,ω) в точці .

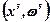Інші види обчислення вектора ξ^s наведені в [20].

3. Знаходимо нове наближення відповідно з рекурентними правилами:

а) у методі стохастичних квазіградієнтів з проектуванням:

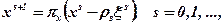(7.36)

де 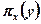— операція проектування;

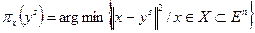; (7.37)

б) у методі стохастичної лінеаризації:

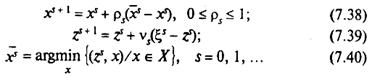
Тут р_s — величина кроку на s-й ітерації; v_s— коефіцієнти, що ви­бираються.

Можна покласти х⁰ = 0 та z⁰ = 0.

Важливою особливістю цих простих і легко реалізованих на ЕОМ методів є той факт, що напрямок «спуску» в них будується на основі випадкового вектора — стохастичного квазіградієнта ξ^s, який є незміщеною оцінкою узагальненого градієнта функції F(x).

Інакше, умовне математичне сподівання

де вектор 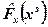задовольняє нерівності:

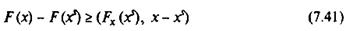
для будь-яких .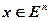

У більш загальному випадку

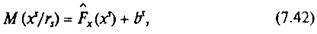
де b^s — зміщення, яке для збіжності методів повинно прямувати до 0 при .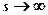

7.5.3. ОДНОПРОДУКТОВІ ЗАДАЧІ УПРАВЛІННЯ ВИРОБНИЦТВОМ

Вважатимемо, що всі продукти, що виробляє підприємство, агреговані в один продукт — валовий. Частина останнього мо­же бути використана в процесі виробництва, а частина — для кінцевого споживання.

Дослідження цих моделей має постійний інтерес і є вихідним матеріалом під час вивчення багатопродуктових моделей.

Розглянемо різні модифікації однопродуктової задачі з об­меженими та необмеженими термінами використання продук­тів. Заслуговує на увагу дослідження задач управління вироб­ництвом з обмеженими термінами використання продуктів, оскільки якість більшості продуктів з часом погіршується. Час­тина таких продуктів часто виявляється досить значною, що викликає необхідність у розробці спеціальних моделей, що враховують факт псування (виходу з ладу, зносу, старіння) продукції під час зберігання.

На деякому підприємстві, потужність якого дорівнює 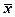, необ­хідно виготовити деякий однорідний продукт обсягом х, попит на який протягом періоду [0,7] характеризується випадковою величиною ω.

Обсяг попиту "ω" в розрахунку на майбутнє будемо трак­тувати як стан середовища. Цей попит може бути будь-яким дійсним числом, отже, множина станів економічного се­родовища 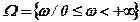. Величина "ω" може складатися з сум заявок n споживачів ω_i, . Останній випадок можна роз­глядати як приклад, коли, знаючи функцію розподілу попиту кожного із споживачів, наштовхуємося на труднощі під час побудови функції розподілу попиту суми споживачів. У той самий час, генеруючи спостереження над реалізаціями випад­кових величин ω_i, можна легко побудувати спостереження над реалізаціями випадкової величини сумарного попиту.

Оскільки попит на вироблену продукцію випадковий, то при обранні будь-якого х можливе як надвиробництво так і недовиробництво (дефіцит). Це типова ситуація, в якій знаходиться підприємство за умов ринкової економіки. Слід обрати х, не знаючи ω, тобто до спостереженого попиту.

Покладемо, що питомі затрати на виробництво (підготов­ку виробництва) продукції складають с грошових одиниць, питомі збитки, пов'язані з можливим надвиробництвом оди­ниці продукції, — α грошових одиниць, а штраф (витрати) за одиницю недовиробництва (незадоволеного попиту) — β гро­шових одиниць.

Тоді затрати, пов'язані з виробництвом та надвиробництвом х одиниць продукції, а також з незадоволеним попитом, за умови, що попит дорівнює "ω", подається функцією

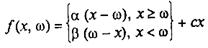
або

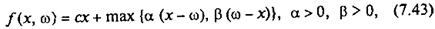
де (х – ω) та (ω – х) — визначають обсяг надвиробництва та недовиробництва продукції.

Легко перевірити, що функція вартості f(x, ω) при фіксованому "ω" є опуклою вниз функцією за х (рис. 7.1).

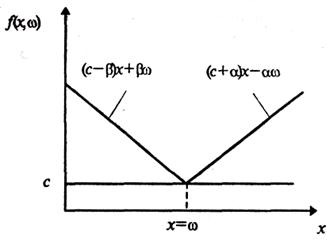
Рис. 7.1. Функція вартості

Ця функція неперервна в усіх точках дійсної осі, але недиференційована при х = ω. Таке співпадання випадковості та недиференційованості в стохастичних економічних моделях швид­ше правило, ніж виняток.

Таким чином, задача полягає у знаходженні такого обсягу випуску продукції х, який мінімізує сумарні затрати, що скла­даються з вартості виробництва, а також сподіваних затрат на надвиробництво та недовиробництво, тобто:

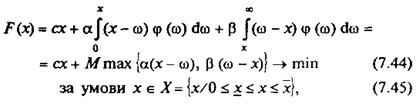
де х — вектор гарантованих потреб в кінцевій продукції системи (замов­лення); 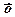— оцінка можливостей потужностей системи на розглядуваний період.

Зауважимо, що функція ризику

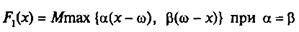
є сподіваним розсіюванням величини ω навколо значення х, а в загальному випадку при α ≠ β розглядається як деяке узагаль­нення сподіваного розсіювання з різноманітними ваговими кое­фіцієнтами перевищення та недосягання рівня х. Неважко побачити, що сформульована задача є частковим випадком опуклої стохастичної одноетапної задачі управління виробництвом (7.32), (7.33). Слід зауважити, якщо вважати α та β випадковими вели­чинами, то одержимо більш загальні постановки задачі.

Розглянемо методи розв'язання поставленої задачі. Звичайний класичний підхід до розв'язання задачі (7.44), (7.45) полягає в наступному. При відсутності обмежень (7.45), тобто у випадку x = E¹, необхідною та достатньою умовою того, що точка х* є розв'язком задачі, буде рівність:

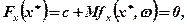
де F_x (x*) — похідна цільовоїфункції F(x) в точці х*; 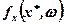— похідна функції 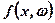в точці по х.

Тоді маємо:

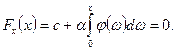
Оскільки

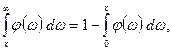
то

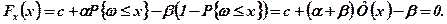
Звідси одержимо, що:

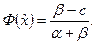(7.46)

де 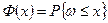— функція розподілу ω, 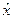— точка мінімуму функції F(x).

Тобто, рівень виробництва визначається за допомогою функ­ції (якщо вона існує), оберненої до функції (7.46), тобто

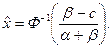
Очевидно, що вираз (7.44) досягає мінімуму при 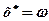. Якщо врахувати обмеження (7.45), то розв'язок одержимо у виді

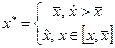(7.47)

Функція (7.44) опукла, але в загальному випадку негладка, бо операція максимізації знаходиться під знаком математичного сподівання. Крім того, вказані вище труднощі для задачі (7.32), (7.33) притаманні і нашій задачі, що звужує область застосування непрямого підходу.

Таким чином, використання наведеного алгоритму доцільно і в даному випадку рекурентне співвідношення (7.36) для задачі (7 44), (7.45) має вид:

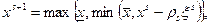(7.48)

оскільки операція проектування 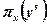точки на множині 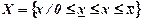здійснюється відповідно до співвідношення .

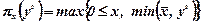У даному випадку стохастичний квазіградієнт функції f(x, ω) обчислюється таким чином:

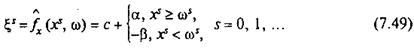
Тут ω^s — незалежне спостереження над величиною попиту, яке може бути одержане в результаті машинного експерименту (імітаційної моделі) або за ω^s може бути взятий s-йелемент з набору статистичних спостережень (даних) відносно вели­чини попиту на даний продукт за різні періоди (роки, місяці, декади тощо). Це можливо у випадку, коли передбачається стаціонарний характер попиту на продукт в період, який роз­глядаємо.

Читайте також:

1. C. 3. Структурна побудова управління організаціями.
2. ERP і управління можливостями бізнесу
3. H) інноваційний менеджмент – це сукупність організаційно-економічних методів управління всіма стадіями інноваційного процесу.
4. III. КОНТРОЛЬ і УПРАВЛІННЯ РЕКЛАМУВАННЯМ
5. ISO9000. Як працює система управління якістю
6. Oracle Управління преміальними
7. А) Задачі, що розкривають зміст дій
8. А. Видання прав актів управління
9. Абстрактна небезпека і концепція допустимого ризику.
10. Автоматизація управління діяльністю готелю
11. АВТОМАТИЗОВАНІ СИСТЕМИ ДИСПЕТЧЕРСЬКОГО УПРАВЛІННЯ
12. АВТОМАТИЗОВАНІ СИСТЕМИ УПРАВЛІННЯ ДОРОЖНІМ РУХОМ

Переглядів: 505