
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
ДВОХЕТАПНІ ЗАДАЧІ УПРАВЛІННЯ ВИРОБНИЦТВОМ ЗА УМОВ РИЗИКУ
В одноетапних задачах, розглянутих раніше, управлінське рішення, що приймається на основі статистичних даних про фактичні значення випадкових параметрів моделей (реалізація у минулі періоди), залишається незмінним після його прийняття. Такий підхід, як вже відзначалося, може призвести до того, що внаслідок здійснення неврахованої, малоймовірної реалізації випадкових параметрів моделі, початкове прийнятий рівень виробництва виявиться невдалим, надто ризикованим.
Характерні особливості прийняття рішень за умов ризику відображає двохетапна схема: рішення — спостереження — рішення, згідно з якою план дій особи, яка приймає рішення, складається з програмної та адаптивної частин.
Можливість плану адаптуватися до змінних умов — необхідна умова його реальної збалансованості та досягнення прийнятного рівня ефективності. Поєднання програмної та адаптивної частин (плану-програми та плану-адаптації) здійснюється згідно з принципами:
1) план-адаптація мусить бути найбільш ефективним для кожної реалізації економічної ситуації;
2) план-програма обирається так, щоб максимізувати сподівану корисність з урахуванням майбутньої адаптації до кожної ситуації.
У загальному випадку раціональна модель щодо прийняття рішень з урахуванням ризику — нелінійна задача двох етапного стохастичного програмування.
При лінійних залежностях між змінними та при інтервально-нейтральній функції корисності з глобальною несхильністю до ризику можна обмежитися двохетапною лінійною задачею стохастичного програмування. Наведемо кілька прикладів.
Приклад. Лінійна двохетапна задача управління виробництвом. Припустимо, що деякий продукт виготовляється на n підприємствах, при його виробництві споживається т ресурсів; b — вектор запасів ресурсів; А — матриця питомих затрат ресурсів при виробництві продукту кожним із підприємств; с — вектор прибутку, який отримано від випуску одиниці продукції. Компоненти матриці А та векторів b та с — випадкові величини, що залежать від стану економічного середовища: А =А(ω), b = b(ω), с = с(ω). Це викликане тим, що немає достовірної інформації про затрати ресурсів при використанні нових технологій, постачання тощо.
Задача полягає у одержанні якомога більшого прибутку при допустимому рівні ризику. Нехай ще є k резервних технологічних способів, D(ω) — матриця виробництва та споживання ресурсів при одиничній інтенсивності кожного резервного технологічного способу яка і послуговує для компенсації, що пов'язана з реалізацією випадкової матриці A(ω) та вектора b(ω). Вектор додаткових затрат (штрафів) при використанні одиниці інтенсивності резервних технологій позначимо через d(ω).
Розв'язання. Позначимо через х — вектор випуску продукції на кожному підприємстві (ці величини необхідно визначити), через у=(у1, ..., у2) — інтенсивності використання резервних технологій.
При відомих реалізаціях  інтенсивності використання резервних технологій у необхідно обирати так, щоб зберігався баланс використання ресурсів, тобто:
інтенсивності використання резервних технологій у необхідно обирати так, щоб зберігався баланс використання ресурсів, тобто:
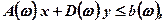 (7.50)
(7.50)
необхідно також накласти умови:
 (7.51)
(7.51)
За цих умов слід визначити такі у, які мінімізували б функцію затрат:
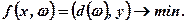 (7.52)
(7.52)
Рішення цієї задачі (задача 2-го етапу) при фіксованих х та ω позначимо через у(х, ω).
Оптимальний же рівень виробництва х* мінімізуємо функцією сумарних затрат F(x), тобто:
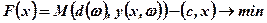 (7.53)
(7.53)
за обмежень
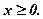 (7.54)
(7.54)
Таким чином, задача (7.50) ... (7.54) є загальною постановкою двохетапної задачі управління виробництвом.
Задача (7.53), (7.54) є задачею першого етапу.
Двохетапну стохастичну задачу вдається звести до задачі лінійного (або нелінійного опуклого) програмування, як правило, лише в тих випадках, коли вектор стану економічного середовища розподілений за дискретним законом зі скінченою множиною можливих результатів. Позначимо через ω1, ..., ωL значення, які приймає випадковий вектор ω, а pi, 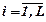 - імовірності подій
- імовірності подій 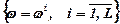 .
.
Відзначимо, що залежність у(х, ω) можна одержати при фіксованому х i вказаному законі розподілу ω таким чином: кожному 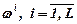 буде відповідати свій розв'язок у(х, ωi)=yi(ω) задачі:
буде відповідати свій розв'язок у(х, ωi)=yi(ω) задачі:
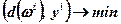 (7.55)
(7.55)
за умов
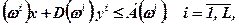 (7.56)
(7.56)
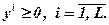 (7.57)
(7.57)
Оскільки при фіксованому х задача (7.55)...(7.57) являє собою взаємно не пов'язані L задач лінійного програмування, то їх спільним розв'язком є вектор (yl(x), ..., у(х)). Цей вектор є розв'язком задачі
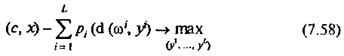
за умов
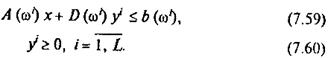
Якщо останню задачу доповнити умовами пошуку такого х, який забезпечить максимальне значення функції цілі, то одержимо таку детерміновану задачу:
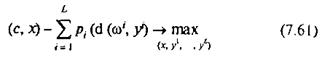
при обмеженнях
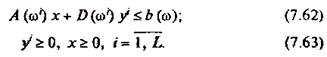
Ця задача є задачею лінійного програмування, якій притаманна велика розмірність (зростає із збільшенням числа L). Враховуючи специфіку обмежень, запропоновано ряд спеціалізованих алгоритмів її розв'язку.
Приклад. Розглянемо двохетапну задачу, де випадковим є лише вектор обмежень b = b(ω), а матриця резервних технологій після певних перестановок рядків та стовпчиків може бути представлена у вигляді D = (E,-E), де Е — одинична матриця.
Аналогічно розіб'ємо вектори у та d на дві частини: у(1), у(2), d(1) та d(2), що відповідають матрицям Е та - Е.
Розв'язання. Двохетапна модель у даному випадку прийме вид:
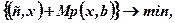 (7.64)
(7.64)
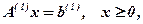 (7.65)
(7.65)
де р (х, b) = min (d(1), y(1) + d(2), y(2)), (7.66)
за умов
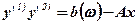 ; (7.67)
; (7.67)
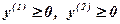 ; (7.68)
; (7.68)
y(1), y(2), d(1), d(2),L - мірні вектори.
Очевидно, що задача (7.66) ... (7.68) (другого етапу) має плани за будь-якої реалізації  та за будь-якого обраного плану х, тобто завжди має розв'язок.
та за будь-якого обраного плану х, тобто завжди має розв'язок.
Задача двоїста до (7.66) ... (7.68) записується так:
 (7.69)
(7.69)
за умов
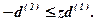 (7.70)
(7.70)
її розв'язок має вид
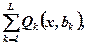 (7.71)
(7.71)
де
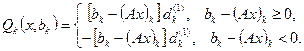 (7.72)
(7.72)
Нехай складові вектора b(ω), тобто bk(ω) рівномірно розподілені на відрізку [γk, δk]. Тоді запишемо вираз для розподілу ймовірностей φ(bk):
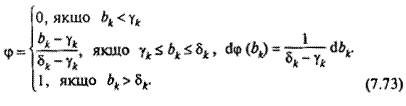
Введемо позначення Ax=W, (Ax)k = wk 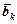 — математичне сподівання вектора правих частин обмежень.
— математичне сподівання вектора правих частин обмежень.
Припустимо, що  . Тоді
. Тоді
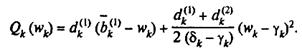
Отже, маємо наступну задачу квадратичного програмування, до якої приведена двохетапна задача стохастичного програмування:
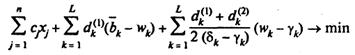 (7.74)
(7.74)
за умов
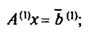 (7.75)
(7.75)
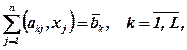 (7.76)
(7.76)
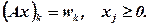 (7.77)
(7.77)
Приклад. Розглянемо задачу, де необхідно при певних обмеженнях мінімізувати затрати ресурсів і яка зводиться до задачі лінійного програмування.
Маємо 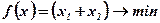 при обмеженнях (х1 - х2)=1, (x1 - 2x2) = 1, та умовах
при обмеженнях (х1 - х2)=1, (x1 - 2x2) = 1, та умовах 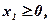
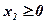 .
.
Розв'язок цієї задачі є очевидним: 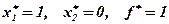 .
.
Зауважимо, що цей розв'язок не зміниться, якщо перше обмеження замінити з рівняння на нерівність, тобто, якщо 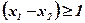 .
.
Нехай тепер права частина першого обмеження є випадковою величиною, тобто b1=1+ω, де ω — рівномірно розподілена випадкова величина на відрізку [ - 1/2, + 1/2]. Вектор х требавідшукати як детермінований.
Розв'язання. Побудуємо двохетапну математичну модель цієї задачі:
 (7.78)
(7.78)
за умов
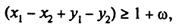 (7.79)
(7.79)
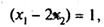 (7.80)
(7.80)
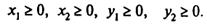 (7.81)
(7.81)
Оскільки лише обмеження (7.79) пов'язане з випадковою зміною правих частин, то в нього додані додаткові змінні у виді різниці невід'ємних змінних, а штрафні коефіцієнти прийняті рівними одиниці.
Розв'язуємо задачу у два етапи.
Необхідно, щоб
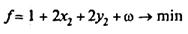 (7.82)
(7.82)
при наступних обмеженнях
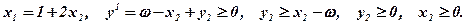 (7.83)
(7.83)
При знаходженні мінімуму функції f за рахунок вибору у2 при фіксованому х2 слід розрізняти два випадки:
1. 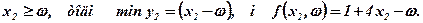
2. 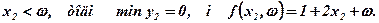
Математичне сподівання по  дає F(х2) = Мf(x2, w), де М — символ математичного сподівання.
дає F(х2) = Мf(x2, w), де М — символ математичного сподівання.
Для випадку, коли 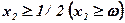 маємо
маємо
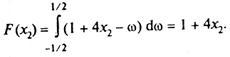
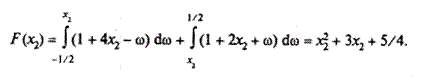 |
Якщо ж
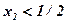 , то при зміні
, то при зміні  будуть мати місце одночасно і випадок 1, і 2, тобто
будуть мати місце одночасно і випадок 1, і 2, тобто
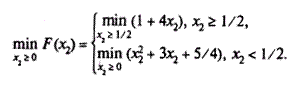 |
Залишається відшукати
Звідси знаходимо, що х2 = 0, x1 = 1, а мінімум функції F дорівнює 5/4.
Читайте також:
- C. 3. Структурна побудова управління організаціями.
- ERP і управління можливостями бізнесу
- H) інноваційний менеджмент – це сукупність організаційно-економічних методів управління всіма стадіями інноваційного процесу.
- III. КОНТРОЛЬ і УПРАВЛІННЯ РЕКЛАМУВАННЯМ
- ISO9000. Як працює система управління якістю
- Oracle Управління преміальними
- А) Задачі, що розкривають зміст дій
- А. Видання прав актів управління
- Абстрактна небезпека і концепція допустимого ризику.
- Автоматизація управління діяльністю готелю
- АВТОМАТИЗОВАНІ СИСТЕМИ ДИСПЕТЧЕРСЬКОГО УПРАВЛІННЯ
- АВТОМАТИЗОВАНІ СИСТЕМИ УПРАВЛІННЯ ДОРОЖНІМ РУХОМ
| <== попередня сторінка | | | наступна сторінка ==> |
| ОДНОЕТАПНІ СТАТИЧНІ ЗАДАЧІ УПРАВЛІННЯ ВИРОБНИЦТВОМ ЗА УМОВ РИЗИКУ | | | ЕЛАСТИЧНІСТЬ РІШЕНЬ |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |