• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Екстремум ф-ї. Необхідна умова існування екстремуму. (Теорема Ферма).

Означення: точка х₀ із області визначення y=f(x) називається точкою min(max) цієї ф-ї , якщо знайдеться дельта окіл в точці х₀ , що для всіх х, що не співпадають із х₀ з цього околу виконується рівність: f(x₀)<f(x), [f(x₀)>f(x)]. Точки Min(max) називаються точками екстремуму. А значення ф-ї в цих точках екстремумом ф-ї. Теорема Ферма: якщо ф-я y=f(x) диференційована в точці х₀ і її околі, а точка х₀ –є точкою екстремуму цієї ф-ї, то похідна в точці х₀=0.Необхідна умова існування екстремумів в більш загальному вигляді формулюється так: якщо ф-я y=f(x) визначена в околі точки х₀ за виключенням може самої точки х₀, має в точці х₀ екстремум, то похідна в цій точці дорівнює нулю або нескінченості. Означення: точки, в яких перша похідна =0, або не існує називаються стаціонарними або критичними точками першого роду. Необхідна умова існування похідної це:

f^/(х)=0 або f^/(х)=+-нескінченості.

56. Достатні умови екстремуму функції однієї змінної.

Перша достатня умова існування екстремуму функції.

Теорема. Якщо ф-ція y=f(x) неперервна в т. х_о і деякому δ-околі цієї т., має похідну, крім, може, в самій т. х_о , тоді –

1) Якщо f’(x) при переході через т. х_о змінює знак з + на - , то х_о - т. максимуму.

2) Якщо f’(x) при переході через т. х_о змінює знак з – на + , то х_о - т. мінімуму.

3) Якщо f’(x) при переході через т. х_о знак не змінює, то х_о не є т. екстремуму.

Доведення. Нехай f’(x) змінює знак з + на – при переході через т. х_о . Покажемо, що т. х_о - т. максимуму.

Якщо похідна змінює свій знак, то це означає, що існує δ>0 (δ-окіл т. х_о ), що

f’(x)>0 для любого х є [х_о - δ; х_о ]

f’(x)<0 для любого х є [х_о ; х_о + δ].

це означає, що на [х_о - δ; х_о ] ф-ція зростає, на [х_о ; х_о + δ] – спадає. Звідси випливає, що зн-ня ф-ції в т. х_о , яке існує в силу неперервності ф-ції в т. х_о є найбільшим на [х_о - δ; х_о +δ]. Отже, т. х_о - т. максимуму.

Друга достатня умова існування екстремуму ф-ції.

Теорема. Якщо ф-ція y=f(x) визначена і двічі диференційована в деякому околі т. х_о , причому f’(x)=0, а f’’(х_о )≠0, то в т. х_о ф-ція

1) має максимум, якщо f’’(х_о )<0

2) має мінімум, якщо f’’(х_о )>0

3) Доведення. Для визначеності будемо вважати, що f’’(х_о )<0. За означенням lim 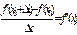. але за умовою теореми f’(x)=0, тоді lim . За припущенням f’’(х_о )<0

. Тоді із означення границі випливає, що в околі деякої т. х_о маємо y’’= lim 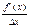<0, 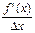<0. Дослідимо цей дріб на знак в залежності від ∆х. y’’<0, коли в чисельнику і знаменнику будуть різні знаки.

y’’(х_о )= lim . <0 - a) ∆f’(x)<0, ∆x>0 → x>х_о

b) ∆f’(x)>0, ∆x<0 → x<х_о .

Таким чином, в т. х_о ф-ція має максимум.

56. Достатні умови екстремуму функції однієї змінної.

Перша достатня умова існування екстремуму функції.

Теорема. Якщо ф-ція y=f(x) неперервна в т. х_о і деякому δ-околі цієї т., має похідну, крім, може, в самій т. х_о , тоді –

4) Якщо f’(x) при переході через т. х_о змінює знак з + на - , то х_о - т. максимуму.

5) Якщо f’(x) при переході через т. х_о змінює знак з – на + , то х_о - т. мінімуму.

6) Якщо f’(x) при переході через т. х_о знак не змінює, то х_о не є т. екстремуму.

Доведення. Нехай f’(x) змінює знак з + на – при переході через т. х_о . Покажемо, що т. х_о - т. максимуму.

Якщо похідна змінює свій знак, то це означає, що існує δ>0 (δ-окіл т. х_о ), що

f’(x)>0 для любого х є [х_о - δ; х_о ]

f’(x)<0 для любого х є [х_о ; х_о + δ].

це означає, що на [х_о - δ; х_о ] ф-ція зростає, на [х_о ; х_о + δ] – спадає. Звідси випливає, що зн-ня ф-ції в т. х_о , яке існує в силу неперервності ф-ції в т. х_о є найбільшим на [х_о - δ; х_о +δ]. Отже, т. х_о - т. максимуму.

Друга достатня умова існування екстремуму ф-ції.

Теорема. Якщо ф-ція y=f(x) визначена і двічі диференційована в деякому околі т. х_о , причому f’(x)=0, а f’’(х_о )≠0, то в т. х_о ф-ція

4) має максимум, якщо f’’(х_о )<0

5) має мінімум, якщо f’’(х_о )>0

6) Доведення. Для визначеності будемо вважати, що f’’(х_о )<0. За означенням lim 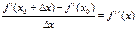. але за умовою теореми f’(x)=0, тоді lim 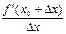. За припущенням f’’(х_о )<0

. Тоді із означення границі випливає, що в околі деякої т. х_о маємо y’’= lim 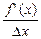<0, <0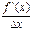. Дослідимо цей дріб на знак в залежності від ∆х. y’’<0, коли в чисельнику і знаменнику будуть різні знаки.

y’’(х_о )= lim . 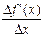<0 - a) ∆f’(x)<0, ∆x>0 → x>х_о

b) ∆f’(x)>0, ∆x<0 → x<х_о .

Таким чином, в т. х_о ф-ція має максимум.

57.Опуклість і угнутість графіка ф-ї. Необхідна і достатня ознаки опуклості графіка ф-ї.

Означення: графік ф-ї y=f(x) називається опуклим на інтервалі (а,в) якщо графік розташований нижче любої дотичної , проведеної до графіка ф-ї в точках інтервала (а,в).Означення: графік ф-ї y=f(x) називається угнутим на відрізку (а,в) якщо графік розташований вище любої дотичної , проведеної до графіка ф-ї в точках інтервала (а,в). Достатня умова опуклості графіка ф-ї: нехай ф-я y=f(x) визначена і двічі неперервно диференційована в точці „х” інтервала (а,в). Тоді, якщо у всіх точках „х” інтервала (а,в) друга похідна у^// >0, то графік ф-ї буде угнутим(U). Якщо для любого „х”, що належить (а,в) у^//<0, то графік ф-ї опуклий(∩).

Читайте також:

1. Автономне існування людини в екстремальних умовах
2. Актуальність і завдання курсу безпека життєдіяльності. 1.1. Проблема безпеки людини в сучасних умовах.
3. Аналіз ефективності реальних інвестиційних проектів в умовах ризику
4. Аналіз та оцінка інвестування в умовах ризику. Якісні та кількісні методи оцінювання проектних ризиків.
5. Аналітична робота в умовах кризи.
6. Аналогічно доводиться достатність умови існування максимуму.
7. Анімізм – уявлення про існування духовних істот та віра в можливість спілкування з ними.
8. АТ – одна з найбільш зручних форм колективного підприємства в умовах ринкової економіки. Першим АТ вважають створену у 1602 році Голандсько –Ост - Індську компанію.
9. Атестація робочих місць з шкідливими і небезпечними умовами праці.
10. Атестація робочих місць за умовами праці
11. Атестація робочих місць за умовами праці
12. Атестація робочих місць за умовами праці

Переглядів: 8909