• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Основні методи обчислення визначеного інтеграла( безпосереднє, частинами).

Безпосереднє інтегрування основане на застосуванні властивостей, таблиці інтегрування і в разі необхідності тотожних перетворень підінтегральної функції.

Інтегрування частинами:

Нехай U i V неперервні на відрізку [a,b], які мають інтегровані похідні на відрізку [a,b].

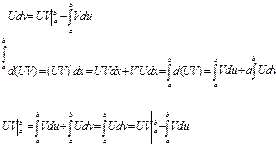
74. Заміна змінної у визначеному інтегралі.

Нехай дано інтеграл , де f(x) неперервна на відрізку [a,b]. Введемо нову змінну t за формулою: х= . Якщо функція х= задовольняє умову :

1.х= і 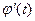неперервна на

2.

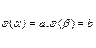
Якщо 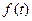неперервна на відрізку [ ], то має місце формула:

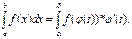
75. Геометричні застосування визначеного інтеграла. Обчислення 1) площі плоских фігур; 2)обємів тіл; 3)довжини дуги кривої.

1) a)Фігура, обмежена графіком неперервної і невідємної на відрізку [a; b] y=f(x), x=a, x=b, y=0: S= 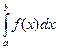(1)

b) Фігура, обмежена неперервною і недодатною на [a; b] ф-цією y=f(x), прямими x=a, x=b, y=0: S=- (2)

с) Фігура, обмежена віссю ОХ, прямими x=a, x=b, графіком ф-ції y=f(x), яка на проміжку [a; b] змінює свій знак скінченне число раз: S= S₁ + S₂ +...+ S_n , де S_і=1, n – знаходиться за формулою (1)

г)Фігура, обмежена графіком 2 неперервних ф-цій f(x) і g(x) на [a; b], x=a, x=b. Причому, f(x)≥ g(x) на [a; b] S=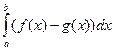

Обчислення площі кривої, заданої параметричними рівняннями

S= 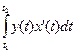, t_1, t ₂ знаходяться з рівняння:

a=x(t_1,), b=x(t_1,)

Обчислення площі в полярній системі координат

Нехай на площині дано т. О (Назвемо її полюсом) і підпряма ОР(полярна вісь) Положення любої т. М на площині можна визначити 2 числами. Числом ρ – що виражає довжину ОМ (радіус-вектор т. М), числом φ – полярним кутом між напрямками полярної осі ОР і радіусом-вектором ОМ. Числа ρ і φ наз. полярними координатами т. М. Якщо ми радіус-вектор будемо вважати додатним, а 0≤ φ≤2π, то кожній т. буде відповідати 1 пара чисел (ρ, φ) і обернено, крім т., де ρ=0, так як φ відповідає любе зн-ня кута φ. Якщо крива, задана в полярних координатах ρ= ρ(φ), то S сектора Р₁ОМ, обмеженої дугою кривої і 2 полярними радіусами О Р₁ і ОМ і відповідає зн-ням кута φ і кута β віразиться інтегралом: S=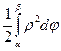

2) a) Нехай потрібно обчислити обєм тіла Т, що знаходиться між 2 перпендикулярними до осі Ох площинами x=a, x=b. Припустимо, що відома площа любого перерізу тіла площиною, перпендикулярною до осі ОХ. Ця площа залежить від положення площі перетину, а отже є ф-цією х. Позначимо її через S(х) і припустимо, що вона неперервна на [a; b]. Розібємо [a; b] на n частин точками так, щоб а=х₀ <х₁< х₂<…< х_i-1< х_i<…< х_n=b. І через т. ділення проведемо площини, перепендикулярні до ОХ. Вони розібють все тіло Т на n шарів. Позначимо через ∆V_i обєм 1 шару, що знаходиться між площинами х = х_і-1 і х = х_і. Тоді обєм цього шару ≈ V_{циліндра}, висота якого ∆ х_і = х_і- х_і-1, а основа співпадає з поперечним перерізом тіла якою-небудь площиною х=ε_і, х_і-1< ε_і< х_і. ∆V_i=S(ε_і)∆ х_і.

V=lim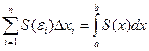

б)Нехай y=f(x) – неперервна на [a; b]. Треба обчислити обєм тіла, утвореного обертанням навколо осі ОХ фігури, обмеженої лініями x=a, x=b, y=f(x), у=0. Так як любий поперечний переріз тіла є круг радіуса r=y, то площа перерізу S(х)=πу².

Тоді V_ox = 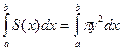V_oy =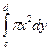

3)Нехай в прямокутній системі координат дано криву y=f(x). Введемо поняття довжини дуги кривої, що знаходиться між вертикальними прямими x=a, x=b.

Розібємо [a; b] на n частин і через т. ділення проведемо паралельні прямі осі ОУ до перетину з y=f(x). Зєднаємо сусідні т. хордами, довжини яких позначимо ∆l_i. Одержимо ламану лінію, вписану в дугу.

Означення. Довжиною дуги наз. та границя, до якої прямує довжина вписаної ламаної, коли довжина найбільшої її ланки прямує до 0.

L= lim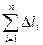

Доведемо, якщо y=f(x) і у’= f(x) – неперервні, то ця границя існує, і разом з тим буде датий спосіб обчислення довжини кривої.

∆у_і = f(х_і) – F(х_і-1)

∆х_і = х_і - х_і-1

∆l_i = =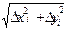

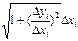
L=

L=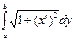

L=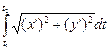

L=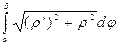

76. Невласні інтеграли І роду. Збіжність 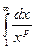. Теореми порівняння.

При визначенні визначеного інтегралу ми припускаєм, що ф-ція f(x) неперервна, а а і b – скінченні числа. Якщо порушена хоч би 1 із цих умов, то інтеграл наз. невласним. Є невласні інтеграли І роду – з нескінченними межами інтегрування від неперервних ф-цій; ІІ роду – з скінченними межами інтегрування від розривних ф-цій.

Означення. Нехай ф-ція f(x) визначена на [a; ∞] і інтегровна на любому відрізку [a; t], t>a, тобто існує 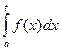при любому t>a. Тоді якщо існує границя lim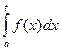 і дор. скінченному числу, то її наз. невласним інтегралом І роду. Позначається - 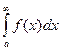(1), тобто (2).

Якщо в (2) він існує, то кажуть, що (1) збігається. Якщо (2) – не існує або дор. ∞, то кажуть, що (1) – є розбіжним.

Аналогічно введем поняття невласного інтегралу 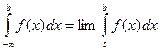(3)

Інтеграл є збіжним, якщот він існує і дор. скінченному числу. Ні – незбіжний.

(4)

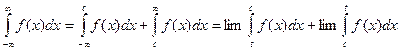
Інтеграл (4) є збіжним, якщо обидва інтеграли в правій частині (4) збіжні, і є розбіжним, якщо хоч би 1 з них є розбіжним.

Теореми порівняння:

Якщо f(x) i g(x) – неперервні на [a; ∞), f(x)≥0 i f(x)≤g(x), то –

1. Якщо 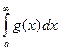- збіжний, то 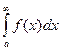- теж збіжний.

2. Якщо 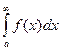- розбіжний, то 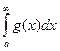- теж розбіжний.

3. Якщо - збіжний, то 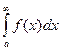- збігається абсолютно.

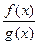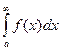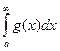4. Якщо lim = k, 0<k<∞, то i одночасно є збіжними або розбіжними.

77. Невласні інтеграли ІІ роду. Збіжність 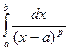. Теореми порівняння.

Якщо ф-ція f(x) неперервна на ]a; b], має нескінченний розрив в т. х=а, тобто lim f(x)=±∞, то тоді вважають, що інтеграл 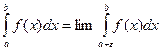, (ε>0) (5)

(5) наз. збіжним, якщо існує скінченна границя в правій частині рівності(5) і наз. розбіжним, якщо дана границя не існує або дор. ∞.

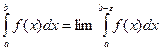, (ε>0) (6)

Якщо ф-ція f(x) неперервна на [a; b], крім т. с (має нескінченний розрив в т.с) (a≤x<c i c<x≤b), тоді –

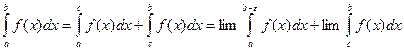(7)

Інтеграл (7) є збіжним, якщо кожний з інтегралів правої частини рівності (7) є збіжним, і розбіжним, якщо хоч би 1 з них інтегралів є розбіжним.

Теореми порівняння.

Якщо ф-ці] f(x) i g(x) неперервні на ]a; b], f(x)≥0, f(x)≤g(x)

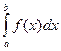1. - збіжний, то і - збіжний.

2. 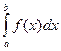- розбіжний, то і - розбіжний.

3. 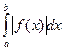- збіжний, то і 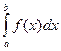- збіжний.

4. lim 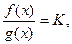0<K<∞, 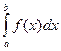i - одночасно збіжні чи розбіжні.

Читайте також:

1. B. Тип, структура, зміст уроку і методика його проведення.
2. Demo 11: Access Methods (методи доступу)
3. I. ЗАГАЛЬНІ МЕТОДИЧНІ ВКАЗІВКИ
4. II. МЕТОДИЧНІ ВКАЗІВКИ
5. II. Основні закономірності ходу і розгалуження судин великого і малого кіл кровообігу
6. II. Основні засоби
7. II. УЧЕБНЫЕ И МЕТОДИЧЕСКИЕ ПОСОБИЯ, ПРАКТИКУМЫ
8. II.3. Основні способи і прийоми досягнення адекватності
9. IV. КЕРІВНИЦТВО, КОНТРОЛЬ І НАДАННЯ ОРГАНІЗАЦІЙНО-МЕТОДИЧНОЇ ДОПОМОГИ ПРАКТИКАНТАМ.
10. IV. Электронное учебно-методическое обеспечение дисциплины.
11. V. ІНДИВІДУАЛЬНІ ЗАВДАННЯ ДЛЯ САМОСТІЙНОЇ РОБОТИ ТА МЕТОДИЧНІ РЕКОМЕНДАЦІЇ ДО ЇХ ВИКОНАННЯ
12. V. Обов'язки методиста кафедри педагогіки

Переглядів: 830